 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вынужденными называются колебания, которые совершаются под действием внешней периодической силы. 12
Простейшим видом колебаний являются гармонические колебания. Это такие движения, когда физические величины изменяются по закону синуса (или косинуса). Гармонические колебания характеризуются периодом, частотой, циклической частотой, амплитудой, фазой, начальной фазой колебаний. Дифференциальное уравнение гармонических колебаний:
дважды продифференцируем его по времени:
Видно, что выполняется следующее соотношение:
19) Скорость колеблющегося тела также меняется по гармоническому закону. Период колебаний скорости такой же, как и период колебаний координаты. V(x)=x’= A*ω*sin(ω*t+φ0)=v(max)*sin(ω*t+φ0) Смещение:
Ускорение: A(x)=x’’=-ω^2*x. Энергия гармонических колебаний:
кинетическая: потенциальная: 20)Гармонический осциллятор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):
Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k , один конец которой жёстко закреплён, а на втором находится груз массы m. Бывает горизонтальным и вертикальным. Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела. Математический маятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Приведённая длина — это условная характеристика физического маятника. Она численно равна длине математического маятника, период которого равен периоду данного физического маятника. Приведённая длина вычисляется следующим образом: 21) Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой что и складываемые колебания. Амплитуда зависит от разности фаз. В результате сложения колебаний мало отличающихся по частоте получаются колебания с периодически меняющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонич. колебаний с близкими частотами, наз. биениями. Биения — явление, возникающее при наложении двух гармонических колебаний, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Биения модулируются по амплитуде. 22) Фигуры Лиссажу: Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна и называется фигурой Лиссажу. Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными. Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз a. 23) Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно уменьшается (затухает). Логарифмический декремент затухания:
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания. 24)Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия. Резонанс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. 12 |
, 
,
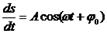
где k — коэффициент жёсткости системы.
- где I — момент инерции относительно точки подвеса, m — масса, a — расстояние от точки подвеса до центра масс.
,β - коэффициент затухания. Добротность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.