 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ
ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩЕНИЯ НА КРЕСТООБРАЗНОМ МАЯТНИКЕ ОБЕРБЕКА
Цель работы: исследование зависимость момента инерции маятника от расположения грузов, закрепленных на стержне маятника. Приборы и принадлежности: маятник Обербека, набор грузов и перегрузов, штангенциркуль.
Теоретические сведения
В механике под твердым телом подразумевают абсолютно твердое тело, т. е. тело деформациями которого можно пренебречь. При вращении твердого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Быстроту вращения характеризуют углом поворота тела в единицы времени. Если за любые равные промежутки времени тело поворачивается на одинаковые углы, вращение называется равномерным. Величина, определяющая изменение угла поворота за единицу времени, называется угловой скоростью. Угловая скорость определяется по формуле
Единицей измерения угловой скорости является рад/с. При неравномерном вращении изменение угловой скорости со временем характеризуется угловым ускорением, которое вычисляется по формуле
Единица измерения углового ускорения является рад/с2. Угловая скорость ω и угловое ускорение ε связаны с линейной скоростью
где При вращении тела вокруг неподвижной оси изменение угловой скорости и его движения зависит от действующего момента силы. Моментом силы
где
Модуль момента силы
где Моментом силы относительно неподвижной оси Равнопеременное вращательное движение тел характеризуется постоянным угловым ускорением, оно появляется под действием сил, момент которых постоянен по величине и направлению. Зависимость углового ускорения от момента силы выражена в основном законе динамики вращательного движения
где Момент инерции
Моментом инерции тела относительно данной оси вращения называют сумму моментов инерции элементарных масс, на которые разбивается тело:
где Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела
Законы вращения тел можно изучить с помощью маятника Обербека.
Если предположить, что нить невесомая, то на диск маятника действует сила
Сила натяжения нити
где Основной закон динамики вращательного движения (2) в скалярном виде и с учетом момента силы (4) примет вид (записаны проекции векторов моментов сил и углового ускорения на ось вращения О,направление которой выбрано «от нас»):
Используя кинематическую связь линейного и углового ускорения (1), а также уравнение движения груза при нулевой начальной скорости
Преобразуем уравнение (5), используя выражение (6) и
Эту зависимость можно использовать для экспериментальной оценки величины момента инерции маятника Обербека. Теоретический расчет момента инерции маятника Обербека представляет сумму моментов инерций
В связи с тем, что размеры грузов малы по сравнению с расстоянием от оси вращения до центров масс грузов, то грузы можно считать материальными точками. Для материальной точки момент инерции равен
где
где
Таким образом, теоретический расчет момент инерции маятника можно представить следующей формулой
Расчет разности моментов инерции
Расчет момента инерции маятника
Описание установки
Для расчетов экспериментального Маятник Обербека имеет вертикальную колонну 1, которая установлена на основании 2. На вертикальной колонне 1 прикреплены два кронштейна: нижний 3 является неподвижным, верхний 4 - подвижный и две неподвижные втулки: нижняя 5 и верхняя 6. Основание снабжено регулируемыми ножками 7, обеспечивающими горизонтальную установку прибора. На верхней втулке 6 посредством основания 8 закреплен подшипниковый узел диска 9 и диск 10. Через диск перекидывается нить 11. Один конец нити прикреплен к двухступенчатому диску 12, а на втором конце закреплены грузы 13. На нижней втулке 5 посредством основания 14 прикреплен тормозной электромагнит 15, который удерживает систему крестовины вместе с грузами в состоянии покоя. Подвижный кронштейн 4 можно переместить вдоль колонны и фиксировать его в любом положении, определяя длину пути падающего груза. Для этого на колонне 1 нанесена миллиметровая шкала 16. На подвижном кронштейне 4 укреплен фотоэлектрический датчик 17. На неподвижном кронштейне 3 - фотоэлектрический датчик 18. К кронштейну 3 прикреплен кронштейн 19 с резиновым амортизатором, ограничивающим движение грузов. Под действием груза нить разматывается и приводит маятник во вращательное движение, которое предполагается равноускоренным. Угловое ускорение при этом тем меньше, чем больше момент инерции системы относительно оси вращения, величина которого зависит от положения перемещаемых грузов на крестовине. Время движения груза
Порядок выполнения работы
1. Установить один перегруз на падающий груз. Определить массу общего падающего груза 2. Измерить с помощью штангенциркуля диаметр диска. Рассчитайте радиус диска 3. Укрепить на стержне крестовины грузы 4. Вращая маятник рукой, намотать нить на диск и установить падающий груз на высоте 5. Включить электронный секундомер. Нажать кнопку «пуск» и одновременно запустить вращение диска. В момент прохождения грузом нижней точки секундомер остановится. Записать время падения 6. Провести прямые пятикратные измерения времени падения груза 7. Изменить расстояние 8. Провести прямые пятикратные измерения времени Таблица
9. Вычислить экспериментальные значения моментов инерции маятника 10. Рассчитать теоретическое значение момента инерции маятника 11. Сравнить полученные результаты и найдите относительную погрешность измерения момента инерции по формуле
где
Контрольные вопросы
1. Дать определение абсолютно твердого тела и вращательного движения. 2. Дать определение средней и мгновенной угловых скоростей, средней и мгновенной угловых ускорений. Единицы измерения угловой скорости и углового ускорения. Как определяется направления векторов угловой скорости и углового ускорения? Какова связь между линейными и угловыми скоростями и ускорениями? 3. Почему движение падающего груза и вращение маховика являются равноускоренными? 4. Вывести основной закон динамики вращательного движения. 5. Что называется моментом силы тела относительно неподвижной точки вращения? Как определяется его направление? В каких единицах он измеряется? 6. Какая сила сообщает вращающий момент маятнику? Как направлен момент этой силы? 7. Что называется моментом инерции материальной точки и тела? В каких единицах он измеряется? Каков физический смысл момента инерции тела. 8. Сформулируйте и объясните теорему Штейнера.
ЛАБОРАТОРНАЯ РАБОТА №2
ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ
Цель работы: изучение колебательного движения тел на примере математического и физического маятников, определение ускорения свободного падения. Приборы и принадлежности: математический маятник, оборотный маятник, электронный счетчик-секундомер.
Теоретические сведения
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Дифференциальное уравнение гармонических колебаний:
или
где m – масса колеблющейся системы; х – смещение этой системы от положения равновесия; k – коэффициент упругости; Решением дифференциального уравнения (1) является уравнение колебательного движения, которое определяют выражением
где х – изменяющаяся величина; t – время; А – амплитуда колебаний, т.е. максимальное отклонение колеблющейся величины от положения равновесия (рис.1);
Фаза колебания – функция времени, она определяет значение изменяющего параметра (х – смещения;
где Если система совершает колебания около положения равновесия без воздействия внешних сил за счет первоначально сообщенной энергии, то такие колебания называются собственными или свободными. Дифференциальное уравнение свободных гармонических колебаний с учетом собственной частоты колебаний
В качестве примера свободных колебаний рассмотрим колебания математического и физического маятников. Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести (рис. 2, а).
В положении равновесия (точка А) сила тяжести В точке С на маятник действует вращающий момент
где L – плечо силы По основному закону динамики вращательного движения
где
или
Полученное уравнение имеет вид, аналогичный дифференциальному уравнению (2), поэтому можно заменить
Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси подвеса О, не проходящей через центр масс тела С (рис. 2,б). При отклонении маятника на угол α составляющая силы тяжести
Возвращающий момент М, создаваемый силой
где L = OC – плечо силы По основному закону динамики вращательного движения
где J – момент инерции маятника относительно оси О. Из формул (8) и (9) имеем
Уравнение (10) аналогично уравнениям (2) и (5), поэтому
Отсюда период собственных колебаний физического маятника
Выражение Приведенной длиной физического маятника называется длина некоторого воображаемого математического маятника, который имеет тот же период колебаний, что и данный физический маятник. С учетом приведенной длины период колебаний физического маятника будет иметь вид
Точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания. Следовательно, при переносе точки под веса в центр качания период колебаний маятника остается прежним. Это положение называется теоремой Гюйгенса. Таким образом, если подобрать у физического маятника такие несимметричные относительно центра тяжести положения двух параллельных осей подвеса, чтобы период колебаний относительно них был одинаков, то расстояние между этими осями будет равно приведенной длине физического маятника. Измерив, это расстояние и период колебаний, можно по формуле (13) найти ускорение свободного падения g.
Описание установки
Маятник, имеющий две параллельные друг другу трехгранные призмы, на которые он может поочередно подвешиваться, называется оборотным маятником. Общий вид установки, включающей в себя математический и оборотный маятники, показан на рис. 4, а.
Основание 1 установки (рис. 4, б) оснащено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, на которой зафиксирован верхний кронштейн 4 и нижний кронштейн 5 с фотоэлектрическим датчиком 6. После отвинчивания воротка 11 кронштейн можно поворачивать вокруг колонки. Натяжение воротка фиксирует кронштейн в любом, произвольно избранном положении. С одной стороны кронштейна 4 находится математический маятник 7, с другой - на вмонтированных вкладышах оборотный маятник 8. Математический маятник представляет собой массивный шарик небольшого радиуса 7, подвешенный на длинной нити для того, чтобы колебания происходили строго в одной плоскости. Длину математического маятника можно регулировать при помощи воротка 9, а его величину можно определить при помощи колонки 3. Оборотный маятник представляет собой стальной стержень 8, на котором могут перемещаться и закрепляться в различных положениях опорные призмы 12 и тяжелые чечевицы 13. Призмы и чечевицы закрепляются приблизительно так, как показано на рис.4,б и маятник подвешивается на кронштейне 4 на одной из призм. На стержне через 10 мм выполнены кольцевые нарезания, служащие для точного определения длины оборотного маятника (расстояние между призмами 12). Нижний кронштейн вместе с фотоэлектрическим датчиком можно перемещать вдоль колонки и фиксировать в произвольно избранном положении. Фотоэлектрический датчик соединен разъемом с привинченным к основанию универсальным миллисекундомером 10.
Порядок выполнения работы
Задание 1. Определение ускорения свободного падения с помощью оборотного маятника.
1. Закрепить чечевицы 13 на стержне оборотного маятника несимметрично, т.е. таким образом, чтобы одна из них находилась вблизи конца стержня, а другая вблизи его середины Призмы маятника 12 закрепить по обеим сторонам центра тяжести, чтобы они были обращены друг к другу лезвиями. Одну из них поместить вблизи свободного конца, а вторую на половине расстояния между чечевицами. Проверить, отвечают ли грани лезвий призм нарезаниям на стержне 2. Закрепить маятник на верхнем кронштейне на грани призмы, находящейся вблизи конца стержня. 3. Нижний кронштейн вместе с фотоэлектрическим датчиком закрепить так, чтобы стержень маятника пересекал оптическую ось. 4. Отклонить маятник на 4-5° от положения равновесия и отпустить. Нажать клавишу "сброс", после подсчета измерителем 9-ти полных колебаний нажать клавишу "стоп". Секундомер покажет время 10 полных колебаний. 5. Повторить пятикратные измерения времени колебания. Результаты измерений записать в табл. 1. 6. Рассчитать период колебаний оборотного маятника Тоб по формуле
7. Снять маятник и закрепить его на второй призме, которая находится посередине стержня. Нижний кронштейн с фотоэлектрическим датчиком переместить так, чтобы маятник пересекал оптическую ось. 8. Отклонить маятник на 4-5° от положения равновесия, измерить время колебания t и сравнить полученный результат со средним временем колебания tоб. 9. Если t > tоб, то вторую призму, расположенную между чечевицами, переместить в направлении чечевицы, находящейся в конце стержня. Если t<tоб, то - в направлении середины стержня. Размещение чечевиц не менять. 10. Повторно измерить время колебаний и сравнить с величиной tоб. Изменять положение второй призмы до момента получения равенства t = tоб с точностью до 0,5%. 11. Получив равенство во времени, повторить пятикратно измерение времени колебания t. Результаты записать в табл.1. 12. Рассчитать период колебаний маятника Тф и занести в табл.1. 13. Определить приведенную длину оборотного маятника Таблица 1
14.Определить ускорение свободного падения gф по формуле
15. Рассчитать абсолютную ошибку измерения ускорения свободного падения g по формулам
16. Записать окончательный результат в виде
Задание 2. Определение ускорения свободного падения с помощью математического маятника.
1.Поворачивая верхний кронштейн, поместить над фотоэлектрическим датчиком математический маятник. 2. Вращая вороток на верхнем кронштейне, установить длину математического маятника 3. Ввести математический маятник в движение, отклоняя шарик на 4-5° от положения покоя. 4. Нажать кнопку "сброс". После подсчета измерителем 9-ти колебаний нажать кнопку "стоп". Результат времени записать в табл. 2. 5. Пятикратно повторить измерение времени колебания и занести в табл. 2. 6. Рассчитать период Тм математического маятника по формуле (14). Сравнить периоды колебаний математического маятника с физическим, вы вычисленным выше.
Таблица 2
7. Рассчитать ускорение свободного падения по формуле
8. Вычислить абсолютную ошибку для ускорения свободного падения gм по формулам (15), (16). 9. Записать окончательный результат в виде 10. Сравнить величины ускорения свободного падения, полученные с помощью математического и физического маятников и сделать соответствующие выводы.
Контрольные вопросы
1. Дать определение понятий: гармоническое колебание, амплитуда, частота, период, фаза, начальная фаза. Записать уравнение гармонического колебания. 2. Нарисовать графики гармонических колебаний, отличающихся друг от друга: - амплитудой, - частотой, - фазой, - начальной фазой. 3. Как определить скорость, ускорение, энергию колеблющейся точки? 4. Что называется физическим маятником, математическим маятником, приведенной длиной физического маятника? 5. Вывести формулы периода колебаний физического и математического маятников. Сравнить их. 6. Сформулировать теорему Гюйгенса. Рассказать, где она применяется в данной работе.
ЛАБОРАТОРНАЯ РАБОТА №3
|



 .
. .
. и линейным (тангенциальным) ускорением
и линейным (тангенциальным) ускорением  следующими соотношениям:
следующими соотношениям: и
и  , (1)
, (1) –расстояние от точек до оси вращения
–расстояние от точек до оси вращения относительно неподвижной точки О называется векторная величина, определяемая векторным произведением радиуса-вектора
относительно неподвижной точки О называется векторная величина, определяемая векторным произведением радиуса-вектора  , проведенного из точки О в точку Априложения силы, на силу
, проведенного из точки О в точку Априложения силы, на силу  (рис. 1).
(рис. 1). ,
, –псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от
–псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от  к
к  .
.

 ,
, –угол между
–угол между  и
и  ;
;  –плечо силы - кратчайшее расстояние между линиями действия силы и точкой О.
–плечо силы - кратчайшее расстояние между линиями действия силы и точкой О. ,называется скалярная величина
,называется скалярная величина 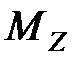 , равная проекции на эту ось вектора момента силы
, равная проекции на эту ось вектора момента силы  , определенного относительно произвольной точки О, данной на оси
, определенного относительно произвольной точки О, данной на оси  (рис. 2). Значение момента
(рис. 2). Значение момента  не зависит от выбора положения точки О на оси
не зависит от выбора положения точки О на оси  .
. , (2)
, (2) - момент инерции тела.
- момент инерции тела. материальной точки относительно какой-либо оси вращения называется скалярная величина, равная произведению массы m этой точки на квадрат расстояния
материальной точки относительно какой-либо оси вращения называется скалярная величина, равная произведению массы m этой точки на квадрат расстояния  от точки до оси вращения:
от точки до оси вращения: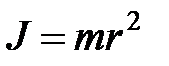 .
. ,
, - элементарная масса;
- элементарная масса;  - расстояние от элементарной массы до оси вращения.
- расстояние от элементарной массы до оси вращения. относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния
относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния  между осями:
между осями: .
. Рис.3
Рис.3 под действием результирующей силы тяжести
под действием результирующей силы тяжести  и силы натяжения нити
и силы натяжения нити  (рис. 3). Запишем для груза второй закон Ньютона в проекции на направление движения:
(рис. 3). Запишем для груза второй закон Ньютона в проекции на направление движения:  Диск вращается равноускоренно под действием натянутой нити, вызванной силой натяжения нити
Диск вращается равноускоренно под действием натянутой нити, вызванной силой натяжения нити  . Сила натяжения передается нитью от груза к диску вращающегося маятника.
. Сила натяжения передается нитью от груза к диску вращающегося маятника. , равная по величине
, равная по величине  и противоположная ей по направлению (следствие третьего закона Ньютона:
и противоположная ей по направлению (следствие третьего закона Ньютона:  ). Отсюда
). Отсюда . (3)
. (3) относительно горизонтальной оси O, направленный вдоль этой оси «от нас» и приводящий в движение маятник Обербека. Величина момента силы равна
относительно горизонтальной оси O, направленный вдоль этой оси «от нас» и приводящий в движение маятник Обербека. Величина момента силы равна , (4)
, (4) – радиус диска, на который намотана нить.
– радиус диска, на который намотана нить. . (5)
. (5) , выразим
, выразим  через величины
через величины  и
и  :
: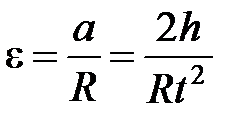 . (6)
. (6) и получим момент инерции маятника Обербека
и получим момент инерции маятника Обербека . (7)
. (7) - момента инерции диска радиусом
- момента инерции диска радиусом  ,
,  - моментов инерции четырех подвижных грузов
- моментов инерции четырех подвижных грузов  и
и  - момента инерции крестовины маятника без груза
- момента инерции крестовины маятника без груза  .
. .
. ,
,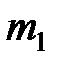 – масса груза на крестовине;
– масса груза на крестовине;  – расстояние от оси вращения до центра грузов. Момент инерции крестовины маятника без груза определяется как
– расстояние от оси вращения до центра грузов. Момент инерции крестовины маятника без груза определяется как ,
,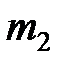 – масса стержня без груза;
– масса стержня без груза; 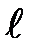 - длина стержня крестовины.
- длина стержня крестовины. .
.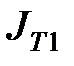 и
и  для двух различных расстояний
для двух различных расстояний  и
и  позволит исключить слагаемые
позволит исключить слагаемые  и
и  . Тогда теоретический расчет момента инерции маятника будет определяться по формуле
. Тогда теоретический расчет момента инерции маятника будет определяться по формуле . (8)
. (8) по формуле (7) при различных расположениях грузов на крестовине можно теоретически проверить величиной момента инерции
по формуле (7) при различных расположениях грузов на крестовине можно теоретически проверить величиной момента инерции  , рассчитанного по формуле (8).
, рассчитанного по формуле (8). измеряется электронным секундомером 18, расположенным у основания прибора, а остановка происходит по сигналу фотодатчика. Груз опускается на расстояние
измеряется электронным секундомером 18, расположенным у основания прибора, а остановка происходит по сигналу фотодатчика. Груз опускается на расстояние  , измеряемое вертикально закрепленной линейкой с сантиметровыми делениями.
, измеряемое вертикально закрепленной линейкой с сантиметровыми делениями.

 и записать в табл.
и записать в табл. и записать в табл..
и записать в табл.. на одинаковых расстояниях
на одинаковых расстояниях  от оси вращения (в пределах от 5 до 15 см). Определите это расстояние, используя деления нанесенные на стержне (1 деление =1 см) и записать в табл.
от оси вращения (в пределах от 5 до 15 см). Определите это расстояние, используя деления нанесенные на стержне (1 деление =1 см) и записать в табл. (в пределах от 30 до 40 см). Значение высоты записать в таб.
(в пределах от 30 до 40 см). Значение высоты записать в таб. груза в табл.
груза в табл.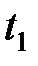 при неизменной геометрии эксперимента согласно п.п. 4-5. Результаты измерений записать в табл. Рассчитать среднее время падения.
при неизменной геометрии эксперимента согласно п.п. 4-5. Результаты измерений записать в табл. Рассчитать среднее время падения. от оси вращения до грузов
от оси вращения до грузов  (в пределах от 20 до 25 см) и записать в табл.
(в пределах от 20 до 25 см) и записать в табл. падения груза при неизменной геометрии эксперимента согласно п.п. 4-5. Результаты измерений записать в табл. Рассчитать среднее время падения.
падения груза при неизменной геометрии эксперимента согласно п.п. 4-5. Результаты измерений записать в табл. Рассчитать среднее время падения. , г
, г , г
, г , см
, см , см
, см , см
, см , c
, c , см
, см , c
, c =
= =
= и
и  с грузами на стержнях, расположенных на разном расстоянии
с грузами на стержнях, расположенных на разном расстоянии  от оси вращения по формуле (7). В качестве времени падения груза взять его среднее значение.
от оси вращения по формуле (7). В качестве времени падения груза взять его среднее значение. для выбранных расстояний
для выбранных расстояний  по формуле (8).
по формуле (8). ,
, - теоретическое изменение моментов инерции при разных расстояниях;
- теоретическое изменение моментов инерции при разных расстояниях;  - экспериментальное изменение моментов инерции при разных расстояниях.
- экспериментальное изменение моментов инерции при разных расстояниях.
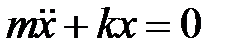 , (1)
, (1) – возвращающая сила.
– возвращающая сила.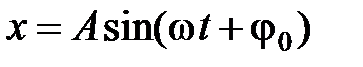 .
. - циклическая (круговая) частота;
- циклическая (круговая) частота;  - начальная фаза.
- начальная фаза. Рис.1
Рис.1 секунд, т.е
секунд, т.е 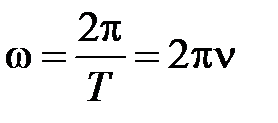 , где Т – период колебаний, т.е. время, за которое совершается одно полное колебание;
, где Т – период колебаний, т.е. время, за которое совершается одно полное колебание; 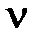 – частота колебаний, т.е. число полных колебаний, совершаемых за единицу времени;
– частота колебаний, т.е. число полных колебаний, совершаемых за единицу времени;  – фаза колебания в момент времени t.
– фаза колебания в момент времени t.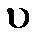 – скорости; а – ускорения) в данный момент времени. Например, фаза определяет, какую часть от амплитуды А составляет смещение х в данный момент времени:
– скорости; а – ускорения) в данный момент времени. Например, фаза определяет, какую часть от амплитуды А составляет смещение х в данный момент времени: ,
, – начальная фаза колебания, т.е. фаза в момент времени t=0.
– начальная фаза колебания, т.е. фаза в момент времени t=0.
 . (2)
. (2)

 уравновешивается силой натяжения нити
уравновешивается силой натяжения нити  . Если маятник отклонить от положения равновесия в точку С на некоторый угол α, то составляющая силы
. Если маятник отклонить от положения равновесия в точку С на некоторый угол α, то составляющая силы  , направленная вдоль нити
, направленная вдоль нити  , уравновесится силой натяжения нити
, уравновесится силой натяжения нити  , перпендикулярная нити, стремится вернуть маятник в положение равновесия. Эта сила является возвращающей силой, или квазиупругой силой. Квазиупругая сила – сила, не упругая по своей природе, но аналогичная упругой силе по виду ее зависимости от смещения, она всегда направлена в сторону, противоположную смещению, и при малых углах отклонения α пропорциональна смещению х.
, перпендикулярная нити, стремится вернуть маятник в положение равновесия. Эта сила является возвращающей силой, или квазиупругой силой. Квазиупругая сила – сила, не упругая по своей природе, но аналогичная упругой силе по виду ее зависимости от смещения, она всегда направлена в сторону, противоположную смещению, и при малых углах отклонения α пропорциональна смещению х. , (3)
, (3)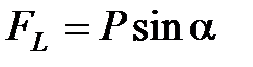 .
. (4)
(4) – момент инерции материальной точки;
– момент инерции материальной точки;  - длина нити. Приравнивая формулы (3) и (4), получим
- длина нити. Приравнивая формулы (3) и (4), получим
 (5)
(5) . Тогда период собственных колебаний математического маятника
. Тогда период собственных колебаний математического маятника . (6)
. (6)
 стремится возвратить маятник в положение равновесия. Для малых углов
стремится возвратить маятник в положение равновесия. Для малых углов 

 . (7)
. (7)
 , (8)
, (8) (9)
(9) ,
,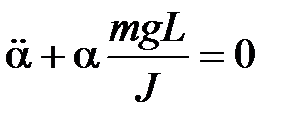 . (10)
. (10) . (11)
. (11) . (12)
. (12) называется приведенной длиной физического маятника.
называется приведенной длиной физического маятника. (13)
(13) Рис. 3
Рис. 3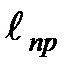 всегда больше L, поэтому точка подвеса и центр качания лежат по разные стороны от центра тяжести.
всегда больше L, поэтому точка подвеса и центр качания лежат по разные стороны от центра тяжести.

 . (14)
. (14) , подсчитывая количество нарезаний на стержне между призмами, которые нанесены через каждые 10 мм.
, подсчитывая количество нарезаний на стержне между призмами, которые нанесены через каждые 10 мм. , с
, с , с
, с .
. (15)
(15) . (16)
. (16) , при α = 0,95.
, при α = 0,95. , равную приведенной длине оборотного маятника
, равную приведенной длине оборотного маятника  (определенной в задании 1). Обратить внимание на то, чтобы черта на шарике была продолжением черты на корпусе фотоэлектрического датчика.
(определенной в задании 1). Обратить внимание на то, чтобы черта на шарике была продолжением черты на корпусе фотоэлектрического датчика. , см
, см , с
, с
 , при α = 0,95.
, при α = 0,95.