 ПОЗНАВАТЕЛЬНОЕ
| Відповідність функції несхильності ОПР до ризику
Видам функції корисності
Визначивши спосіб побудови функції корисності, ми можемо використовувати цю теорію для визначення так званої премії за ризик і за несхильність до ризику. Премією за ризикназиваєтьсясума (в одиницях виміру х), якою суб'єкт управління може поступитися із середнього виграшу за те, щоб уникнути ризику, пов'язаного з лотереєю:
А ступінь несхильності до ризикурозраховується як:
Практичні завдання до теми 2: 2.1. Дайте визначення таким термінам: 2.1.1. Ймовірність 2.1.2. Випадкова змінна 2.1.3. Розподіл ймовірностей 2.1.4. Взаємовиключні події 2.1.5. Незалежні події 2.1.6. Дискретна випадкова подія 2.1.7. Безперервна випадкова подія 2.1.8. Нормальний розподіл ймовірностей 2.1.9. Стандартизована (нормована) змінна 2.1.10. Логнормальний розподіл ймовірностей 2.1.11. Розподіл ймовірностей Пуасона 2.1.12. Довірчий інтервал 2.1.13. Економічний капітал 2.1.14. Експозиція 2.1.15. Корисність 2.1.16. Функція розподілу (або інтегральний закон розподілу) 2.1.17. Варіація 2.1.18. Дисперсія 2.1.19. Достовірна подія 2.1.20. Математичне очікування 2.1.21. Випробування 2.1.22. Особа, яка приймає рішення 2.1.23. Капітал під ризиком (ризиковий капітал) 2.1.24. Шокова величина 2.1.25. Стрес-тестування 2.1.26. Метод Монте – Карло 2.1.27. Культурна теорія ризику
2.2. Логіко-структурні схеми: 2.2.1. У формі таблиці представте підходи до якісної оцінки фінансових ризиків та їх особливостей для страхових кампаній, банків, інвестиційних фондів, пенсійних фондів. 2.2.2. У формі таблиці представте підходи до якісної оцінки фінансових ризиків та їх особливості для різних видів банків залежно від спрямування їх діяльності (інвестиційних, ощадних тощо). 2.2.3. У вигляді схеми наведіть види показників оцінки фінансових ризиків та їх призначення щодо мінімізації різних видів фінансових ризиків. 2.2.4. У вигляді схеми побутувати логіку взаємозв'язку (взаємовпливу) між різними методами оцінки фінансових ризиків.
2.3. Тестові завдання: 2.3.1. Висновок про ступінь припустимості ризику робиться на підставі: А) якісного аналізу; Б) експертного аналізу; В) кількісного аналізу; Г) усі відповіді правильні. 2.3.2. Ступінь чи міра можливості випадкової події визначається на підставі розрахунку: А) граничного рівня ризику; Б) граничного рівня ризику; Г) ймовірності; В) квантиля. 2.3.3. Змінна з невизначеною поведінкою називається: А) невизначеною; Б) випадковою; В) квазізмінною; Г) недетермінованою. 2.3.4. У разі, якщо можливі невизначені результати відомі та рівноймовірні, розраховується: А) емпірична ймовірність; Б) статистична ймовірність; В) апріорна ймовірність; Г) суб'єктивна ймовірність. 2.3.5. У разі, якщо ймовірність оцінюється відношенням кількості випадків, в яких відбулася ця подія, до загальної кількості випробувань, така ймовірність є: А) класичною; Б) суб'єктивною; В) емпіричною; Г) апостеріорною. 2.3.6. На підставі думки експертів розраховується ймовірність: А) емпірична; Б) суб'єктивна; В) експертна; Г) апостеріорна. 2.3.7. Ймовірність настання хоча б однієї з взаємовиключних подій А та Б дорівнює: А) Р(А або В) = Р(А) + Р(В) – Р(А и В); Б) Р(А та В) = Р(А В) Р(А або В) = Р(А Г) Р(А та В) = Р(А) * Р(В|A). 2.3.8. Ймовірність настання хоча б однієї з взаємовиключних подій А та Б дорівнює: А) Р(А або В) = Р(А Б) Р(А або В) = Р(А) * Р(В|A); В) Р(А або В) = Р(А Г) Р(А або В) = Р(А) + Р(В) – Р(А и В). 2.3.9. Дві ризикових події є незалежними, якщо: А) поява однієї призводить до неможливості настання іншої події; Б) події не можуть відбутися одночасно; В) події можуть відбутися одночасно; Г) ймовірність появи однієї події впливає на спроможність появи іншої. 2.3.10 Дві ризикових події є взаємовиключними, якщо: А) ймовірність появи однієї події впливає на можливість появи іншої; Б) поява однієї призводить до неможливості іншої події; В) для них є суттєвою умовна ймовірність; Г) ймовірність їх спільного настання визначається на підставі помноження ймовірностей їх реалізації. 2.3.11. Ймовірність зростання вартості акції А дорівнює 30%, вартості акції Б – 60%. Ймовірність одночасного зростання вартості цих акцій – 50%. Тоді ймовірність того, що відбудеться зростання вартості хоча б однієї з таких акцій складатиме: А) 90%; Б) 40%; В) 50%; Г) 20%. 2.3.12. Ймовірність зростання вартості акції дорівнює 25%, вартості облігації – 30%. Ймовірність того, що відбудеться зростання вартості хоча б одного із цих цінних паперів – 40%. Тоді ймовірність одночасного зростання їх вартості складатиме: А) 40%; Б) 55%; В) 15%; Г) 10%. 2.3.13. Ймовірність зростання курсу долару США, що обумовлена зростанням процентних ставок складатиме 35%. Передбачена можливість зростання курсу долару складатиме 18%, процентних ставок – 10%. Тоді ймовірність одночасного підвищення даних фінансових параметрів складатиме: А) 6,3%; Б) 53%; В) 28%; Г) 3,5%. 2.3.14. Розподіл ймовірностей податкового ризику є: А) безперервним; Б) нормальним; В) дискретним; Г) стандартним. 2.3.15. Безперервний розподіл ймовірностей не можна використати для: А) ризику зниження грошових надходжень підприємства; Б) кредитного ризику; В) валютного ризику; Г) правильних відповідей немає. 2.4. Ситуаційні завдання та задачі: 2.4.1 Кинуто стандартну шестигранну кістку. Яка ймовірність того, що випаде: А) чотири; Б) не чотири; В) менш чотирьох; Г) сім.
2.4.2. Якщо S – множина натуральних чисел – менш 12, класифікуйте такі пари підмножин як взаємовиключні та/або вичерпувані: 1) {парні}, {непарні}; 2) {кратні 3}, {кратні 4}; 3) {1,2,3}, {≥3}; 4) {1,2,3}, {4,5,6}; Розрахувати ймовірність того, що випадково обраний член множини S буде членом кожної з 8 наведених підмножин.
2.4.3. Випадково обирається число з множини {1,2,3,4,5,6,7,8,9}. а) розрахуйте ймовірність того, що обране число буде більше 5; б) розрахуйте ймовірність того, що обране число буде більше 7 та непарне; в) використовуючи відповіді а) та б), розрахуйте ймовірність того, що обране число буде непарним за умови, що воно більше 5.
2.4.4. Огляд рахунків 400 інвесторів на фондовій біржі надав таку інформацію про число впродовж останнього кварталу:
Завдання: а) побудуйте графік розподілу Х; б) визначте ймовірність того, що випадково обраний інвестор зробив: - нуль угод; - у крайньому разі, одну угоду; - більше п'яти угод; - менше шести угод. в) визначте маточікування та дисперсію числа угод.
2.4.5. Поточну ціну акції можна було б приблизно змоделювати за допомогою нормального розподілу з маточікуванням 15,28 грн. та середнім квадратичним відхиленням, що дорівнює 0,12 грн. Розрахуйте ймовірності того, що ціна буде: а) не нижчою за 15,5 грн.; б) не вищою за 15 грн.; в) між 15,1 та 15,4 грн.; г) між 15,05 грн. та 15.10 грн.
2.4.6. Ціна цінного папера нормально розподілена. Упродовж останнього року протягом 20% робочих днів вона була нижчою за 20 грн. У 75% випадків ціна була вищою за 25 грн. Знайдіть маточікування та середньоквадратичне відхилення ціни.
2.4.7. Визначте ймовірність того, що фінансовий актив, доходність якого нормально розподілена, принесе дохід від 3,5% до 8%. Середня величина доходу складає 4%, а середнє квадратичне відхилення – 3%.
2.4.8. Щоденна дохідність цінного паперу нормально розподілена з маточікуванням, що дорівнює 7% та середнім квадратичним відхиленням 2%. Визначте ймовірність того, що щоденна дохідність буде більше 12%.
2.4.9. Поточна вартість акції 15 грн. У наступний Т1 вона може піднятися з ймовірністю 45% на 15%, та з ймовірністю 55% упасти в ціні на 20%. Визначте можливі витоки (результати) на момент Т3, а також маточікування ціни такої акції.
2.4.10. Ймовірність зростання вартості акції дорівнює 15%, вартості облігації – 20%. Ймовірність того, що відбудеться зростання вартості хоча б одного з цих цінних паперів – 30%. Визначте ймовірність одночасного зростання вартості акції.
2.4.11. Ймовірність зростання вартості акції А дорівнює 25%, вартості акції Б – 50%. Ймовірність одночасного зростання вартості цих акцій – 45%. Визначте ймовірність такого зростання вартості хоча б однієї з цих акцій.
2.4.12. Ймовірність зростання курсу долару США, що обумовлена зростанням відсоткових ставок, складає 25%. Передбачена можливість зростання курсу долару складає 14%, відсоткових ставок – 8%. Визначте ймовірність одночасного підвищення таких фінансових параметрів.
2.4.13. Маточікування доходів підприємства складає 1 600 тис. грн.; середньоквадратичне відхилення – 550 тис. грн. Припускається, що розподіл ймовірностей доходів підприємства має нормальний закон розподілу. Залежно від розміру шкоди визначено такі види та розміри можливих збитків підприємств: - катастрофічні збитки – 1600 тис. грн.; - критичні збитки – 1000 тис. грн.; - припустимі збитки – 300 тис. грн. Визначте ймовірність, з якою величина доходів підприємства може знизитися до рівня катастрофічних, критичних та припустимих збитків.
2.4.14. Поточний курс долара США – 8 грн. за 1 дол., середньоквадратичне відхилення – 0,75 грн., довірчий інтервал – 99%. У банка довга відкрита позиція у розмірі 5 млн. дол. США. Визначте показник вартості під ризиком (VaR).
2.4.15. Відношення до ризику особи, що приймає рішення, характеризується такою функцією корисності: U(x) = 1,5x2, Необхідно визначити очікуваний грошовий виграш, гарантовану суму (БДЭ) та премію за ризик для лотереї: А (кращий вихід подій) = 17, а (гірший вихід подій) = 3; р (ймовірність кращого виходу) = 0,6.
2.4.16. Функція корисності особи, що приймає рішення, має вигляд: U(x)=25+2x. Ця особа розглядає альтернативу вкладення коштів у визначений вид цінних паперів: вкласти 25 тис. грн. та з ймовірністю 60% отримати прибуток від операції у розмірі 37 тис. грн., з ймовірністю 40% втрачає весь капітал. На підставі функції корисності визначити, чи слід їй здійснювати інвестування в такі цінні папери.
2.4.17. Функція корисності особи, яка приймає рішення, може бути представлена:
Мають місце три альтернативних вкладення у цінні папери: 1) вкладення в облігацію принесуть гарантований прибуток у розмірі 2 грн.; 2) вкладення в акцію підприємства А принесуть прибуток у розмірі 3 грн. з ймовірністю 0,5 або 1 грн. з ймовірністю 0,5; 3) вкладення в акцію підприємства Б принесуть прибуток у розмірі 4 грн. на акцію з ймовірністю 0,5 або взагалі не принесуть дохід з ймовірністю 0,5. Який варіант вкладень обере особа?
2.5. Творчо-аналітичні завдання: 2.5.1. Згідно з даними про індекс ПФТС за останні 2 місяці розрахуйте: а) середнє значення індексу; б) розмах варіації (різниця між максимальним та мінімальним значеннями); в) волатильність індексу (історичну волатильність). 2.5.2. Згідно з даними про офіційний курс гривні до долару США за останні 2 місяці розрахуйте: а) середнє значення курсу; б) розмах варіації (різницю між максимальним та мінімальним значеннями); в) волатильність курсу (історичну волатильність). 2.5.3. Згідно з даними про офіційний курс гривні до євро за останні 2 місяці розрахуйте: а) середнє значення курсу; б) розмах варіації (різницю між максимальним та мінімальним значеннями); в) волатильність курсу (історичну волатильність).
[1] Це формула поєднання (одного з видів поєднань) - з n різних елементів складаються групи по j елементів у кожній, незважаючи на порядок елементів у групі |



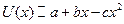 (c>0;
(c>0;  )
)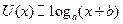

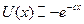 c>0
c>0 )
) c>0
c>0 b>0
b>0



 В) = Р(А) * Р(В);
В) = Р(А) * Р(В); В) = Р(А) + Р(В);
В) = Р(А) + Р(В);