 ПОЗНАВАТЕЛЬНОЕ
| Загальні підходи до кількісної оцінки фінансових ризиків
ТЕМА 2. ОСНОВИ ОЦІНКИ ФІНАНСОВИХ РИЗИКІВ Одержати прибуток не ризикуючи, набути досвід не піддаючись небезпеці, здобути нагороди не працюючи – настільки ж неможливо, як жити, не будучи народженим. Сенека 1. Загальні підходи до кількісної оцінки фінансових ризиків. 2. Показники оцінки фінансових ризиків. 3. Врахування ступеня схильності до ризику. Функція корисності.
Література [1,13,14, 27, 31, 41, 44, 50, 66 ]
Загальні підходи до кількісної оцінки фінансових ризиків
Невід'ємною функцією управління фінансовими ризиками є їх оцінка з метою: - визначення ступеня його допустимості або неприпустимості; - ухвалення рішення щодо вибору тієї або іншої фінансової операції (фінансового) з урахуванням їх ступеня ризикованості; - визначення обсягу резервного капіталу або загального обсягу власного капіталу як джерела відшкодування фінансових втрат; - визначення ступеня відповідності діяльності фінансової установи нормативним вимогам органів контролю тощо.
Оцінка рівня ризику традиційно здійснюється за допомогою аналізу. Виділяють два види такого аналізу: 1. Якісний аналіз фінансових ризиків – його результатом є виявлені види фінансових ризиків, характерні для діяльності суб'єкта економіки, а також взаємозв'язок між ними. 2. Кількісний аналіз фінансових ризиків – його результатом є ступінь ризикованості того або іншого об'єкта, а також висновок про ступінь допустимості ризику. Такі види аналізу здійснюються послідовно і не є взаємовиключними або самодостатніми. Вихідним поняттям, а також елементом оцінки будь-якого виду ризику (у тому числі і фінансового) є ймовірність реалізації тієї або іншої випадкової події. Ймовірність –цеступінь можливості виникнення ризикової (випадкової) події.
Залежно від способу її оцінки виділяють такі види ймовірності: 1) класична ймовірність (апріорі). Застосовується в тих випадках, коли можливі невизначені результати відомі й однаково ймовірні (підкидання монети, гральної кістки). Тоді ймовірність події дорівнює:
де до – число однаково ймовірних результатів, пов'язаних з подією; ДО – загальне число можливих результатів; Р(А) – ймовірність події А. Для оцінки фінансових ризиків цей тип ймовірності не використовується. 2) емпірична (статистична) ймовірність.Виражається відношенням числа результатів n, в яких випала ця подія, до загального числа результатів (спроб) - N. У статистиці розраховується як показник частоти:
Статистична ймовірність узагальнює (і уточнює) поняття класичної ймовірності у разі нескінченного числа спроб, тобто:
За умови прагнення числа до нескінченності статистична ймовірність стає класичною. В оцінці фінансових ризиків може широко використовуватися для визначення ймовірності реалізації випадкових подій у короткостроковому і середньостроковому періодах. 2) Суб'єктивна ймовірність застосовується у випадку, коли класичну і статистичну ймовірності неможливо застосувати (наприклад, у випадку експертного опитування). Така ймовірність встановлюється не в результаті збирання та обробки масивів спроб, а в результаті певної процедури узагальнення суб'єктивних думок експертів. Є фактично ступенем упевненості в настанні тієї або іншої події.
На прийняття рішень в умовах ризику значно впливає рівень і специфіка освіти. Соціологічні дослідження вказують на різний обсяг необхідної додаткової інформації при прийнятті рішень в умовах ризику: 1) англосаксонська освіта є переважно гуманітарною. Люди з такою освітою набагато менше схильні очікувати на додаткову інформації для прийняття рішень. Звідси й більша схильність до прийняття інтуїтивних рішень; 2) представникам континентальної Європи потрібний набагато більший обсяг інформації. Освіта за французькою моделлю, що надає особливе значення точним наукам – з раннього дитинства в європейцях виховується віра в те, що в основі світу − те, що піддається обчисленню; 3) у більшості східних культур рішенням дають «вилежатися», тут менше чекають на нову інформацію, але більше зусиль докладається на переосмислення ситуації; 4) для слов'ян характерна потреба в зайвій інформації, що часто затягує ухвалення рішення, сповільнює усвідомлення того, що відбувається. Іншим аспектом є виникнення хибного почуття захищеності при присвоєнні випадковим подіям невеликої ймовірності.
Основні дії з ймовірностями окремих випадкових подій підпорядковуються таким правилам теорії ймовірностей: 1. Правило додавання застосовується до взаємовиключних подій (може бути або подія А або подія Б). Визначається ймовірність настання хоча б однієї з них:
де Р(А) – ймовірність події А; Р(Б) – ймовірність події Б.
2. Правило додавання для взаємоневиключних подій (за умови, що певні події могли спричинити результат А, певні − результат Б, а певні − обидва одночасно). Ймовірність того, що може відбутися хоча б одна з подій А або Б:
Р(А або В) = Р(А) + Р(В) – Р(А и В).
3. Правило множення для незалежних подій використовується у разі необхідності визначення ймовірності настання і події А, і події В за умови їх незалежності:
Р (А і В) = Р(А
де
4. Правило множення залежних подій використовується у разі необхідності визначення ймовірності подій А і Б за умови їх залежності: Р(А и В) = Р(А) * Р(В|A),
Випадкова змінна визначається її розподілом ймовірностей і можливими значеннями такої змінної. При цьому розподіл ймовірностей – це математична модель ймовірності випадкових подій. Для задавання виду розподілу ймовірностей необхідно знати тип випадкової змінної. Існує два типи випадкових змінних: - дискретні – ті, які мають кінцеве число можливих результатів; - безперервні – це такі випадкові змінні, які можуть набувати нескінченне число значень. Дискретним розподілом ймовірностей називається такий розподіл ймовірностей, за якого вони набувають тільки певних дискретних значень. Дискретні випадкові змінні мають кінцеве число можливих результатів. Прикладами дискретних розподілів ймовірностей є біноміальні й триноміальні розподіли. Ймовірності разом з пов'язаними з ними значеннями випадкової змінної є функцією частот ймовірностей. При безперервному розподілі ймовірностей змінні ймовірностей можуть набувати будь-якого значення в межах певного інтервалу. Безперервні випадкові змінні можуть мати нескінченну кількість значень (наприклад, швидкість, час, відстань, рентабельність активів, курс валюти тощо). Функція щільності ймовірностей є функцією, що репрезентує ймовірність випадкової змінної. Графік щільності розподілу ймовірності зображено на рис. 2.1:
Рис. 2.1. Графік нормального розподілу ймовірності (розподіл Гаусса)
Площа будь-якого вертикального сегмента під кривою є ймовірністю того, що нормально розподілена випадкова величина набуде значення на інтервалі, обмеженому цим сегментом. Функція нормального розподілу ймовірності має такі властивості: - максимум такої функції (максимально ймовірна величина) знаходиться у точці х = μ (математичного очікування); - «розтягнутість» уздовж осі х визначається параметром σ; - щільність ймовірності нормального розподілу дорівнює:
де σ – середньоквадратичне відхилення. - функція розподілу дорівнює:
Для того, щоб знайти ймовірність того, що нормально розподілена випадкова величина X потрапить в інтервал - знайти відповідний інтервал для нормально розподіленої випадкової величини
- потім за таблицею знайти значення функції розподілу F(z1) і F(z2) і визначити ймовірність потрапляння випадкової величини в заданий інтервал:
яка збігається із шуканою ймовірністю потрапляння випадкової величини в заданий інтервал. Зворотне завдання: знайти інтервал, у який потрапляє нормально розподілена випадкова величина із заданою ймовірністю.
Такий спосіб розв'язання зручно використовувати у разі, коли випадкова величина є величиною збитків суб'єкта господарювання. Тоді завдання визначення ймовірності потрапляння випадкової величини у визначений інтервал розв’язується зазначеним вище способом. Криву щільності розподілу ймовірностей випадкових збитківпоказано на рис. 2.3:
Рис. 2.3. Графік кривої щільності розподілу ймовірностей випадкових збитків При цьому ймовірність припустимих збитків дорівнює Крива розподілу ймовірностей F(x)–вказує на ймовірність не перевищення певного рівня збитків (у загальному випадку – певних значень випадкової величини). Криву розподілу ймовірностей показано на рис. 2.2:
Рис. 2.2. Графік функції розподілу (крива розподілу ймовірностей)
Відповідно до нерівності Чебишева ймовірність того, що випадкова величина відхиляється за модулем від свого математичного очікування більш ніж на задану величину α, не перевищує її дисперсії, поділеної на α2:
Нерівність Чебишева визначає тільки верхню оцінку можливого відношення. Вище за цю оцінку ймовірності не може бути ні за яким законом розподілу ймовірностей. На практиці ж випадкові числа дуже рідко виходять за межі
Дуже часто розподіл ймовірностей, що відбиває фінансові показники або змінні, не є нормальним. У такому разі перевірка на адекватність розподілувключає перевірку на асиметрію й ексцес. При цьому коефіцієнти асиметрії й ексцесу дозволяють зробити попередні висновки про наближення досліджуваного розподілу до нормального. Асиметричність вказує на рівень скошення (рис. 2.4).
Рис. 2.4. Приклади графіка позитивної і негативної асиметрій
Коефіцієнт асиметрії розраховується таким чином:
При цьому чисельник – це центральний момент 3-го порядку, знаменник – центральний момент 2-го порядку. Значення отриманого коефіцієнта свідчать про таке: - якщо Ка = 0 – розподіл рівномірний; - якщо Ка ≥ 0 – розподіл з правою асиметрією; - якщо Ка ≤ 0 – розподіл з лівою асиметрією. Ексцесвідбиває ступінь піковості (гостровершинності) розподілу ймовірностей випадкової змінної.
Рис. 2.5. Розподіли ймовірностей з різним ступенем гостровершинності
Коефіцієнт ексцесу розраховується таким чином:
У випадку, якщо Ке = 3, то розподіл рівномірний.
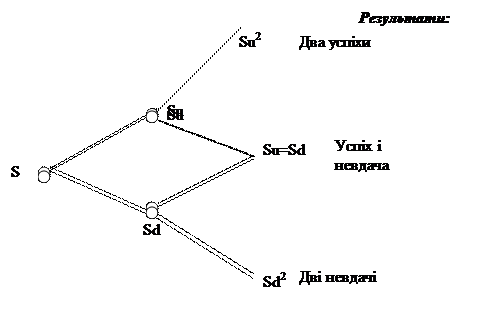
Одним з найбільш важливих розподілів у фінансах є біноміальний розподіл. Для формування біноміального розподілу випадкова змінна повинна відповідати таким умовам: 1) у кожен момент часу змінна може отримати тільки одне з двох значень у результаті однієї з двох подій, одна з яких називається «успіх», а інша - «невдача». Подію і момент часу, коли це відбулося, прийнято називати «біноміальною спробою»; 2) для кожної послідовності спроб ймовірність успіху і невдачі постійна; 3) усі спроби ідентичні; 4) усі спроби незалежні. Біноміальна випадкова змінна – це число успіхів у результаті певної кількості незалежних спроб n. Ймовірність успіху в кожній спробі дорівнює p. Кажуть X-Біном (n,p), де Х – число успіхів у n спробах, отримує значення від 0 до n. Таким чином, для n-спроб може бути n+1 результат. У випадку двох біноміальних спроб утворюється три результати. Біноміальне дерево буде таким:
j – кількість успіхів.
Рис. 2.6. Біноміальне дерево двох спроб з утворенням трьох результатів Біноміальний розподіл визначає ймовірності Х для кожного результату. Ймовірність досягнення кожного з них залежить від ймовірності успіху (тобто р) і загального числа способів досягнення результатів. Для знаходження ймовірностей необхідно знати кількість результатів, що мають певне число успіхів. Кількість j-успіхів для заданого числа n біноміальних спроб, використовуючи формулу[1] :
де n – число біноміальних спроб; j – число успіхів, при цьому Ймовірність одержання j успіхів із n спроб становить:
де р – ймовірність успіху; 1-р – ймовірність невдачі.
Тоді дисперсія біноміального розподілу дорівнюватиме:
|




 ,
, .
. .
.
 Р(А або В) = Р(А
Р(А або В) = Р(А  В) = Р(А) + Р(В),
В) = Р(А) + Р(В),

 В) = Р(А) * Р(В),
В) = Р(А) * Р(В),
 де Р(В|A) – умовна ймовірність того, що реалізується подія Б за настання А.
де Р(В|A) – умовна ймовірність того, що реалізується подія Б за настання А.
 ;
;  ,
, .
. , необхідно:
, необхідно: (стандартизованої або нормованої змінної):
(стандартизованої або нормованої змінної): ;
;  ;
;
 ,
,


 , а ймовірність критичних збитків дорівнює
, а ймовірність критичних збитків дорівнює  і т.д.
і т.д.
 .
. . Так, для нормального розподілу ця ймовірність приблизно дорівнює 0,003.
. Так, для нормального розподілу ця ймовірність приблизно дорівнює 0,003.
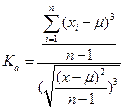 .
.
 .
.
 ,
, – кількість способів досягнення j успіхів з n спроб;
– кількість способів досягнення j успіхів з n спроб;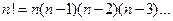
 ,
,


