 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Параллельная сортировка Бэтчера
Курсовая работа «Параллельные алгоритмы обработки данных»
Выполнил: студент группы РТЭ 11-10 Садовникова Т.В. Проверил: Серолапкин А.В.
Чебоксары 2012
Содержание: 1)Аннотация 2)Введение 3)Параллельная сортировка Бэтчера 4)Умножение матриц 5)Заключение 6)Литература
Аннотация
Работа посвящена вопросам использования параллельных алгоритмов для создания современных эффективных программных решений. Актуальность данной тематики обусловлена снижением темпов роста тактовой частоты микропроцессоров и возрастанием внимания к использованию всех возможностей многоядерных и многопроцессорных систем. В работе рассмотрен ряд базовых параллельных алгоритмов, таких как умножение матриц, параллельная сортировка Бэтчера. Приведена реализация этих алгоритмов c использованием языка программирования Си++. Введение В ближайшее время под эффективным использованием аппаратных средств компьютера будут пониматься применение параллельных алгоритмов. Это связано с замедлением темпов роста тактовой частоты микропроцессоров и быстрым распространением многоядерных микропроцессоров. Создание эффективных программных решений для параллельных систем складывается из трех основных компонентов: параллельных алгоритмов, средств реализации параллельности и систем отладки. Под средствами реализации параллельности понимаются языки программирования или библиотеки, обеспечивающие инфраструктуру параллельных программ. Таких система достаточно много. К ним можно отнести: Occam, MPI, HPF, OpenMP, DVM, OpenTS, Boost.Thread, Posix Threads. Сюда также можно отнести библиотеку Integrated Performance Primitives компании Intel. Поскольку отладка параллельной программы является процессом более трудоемким, чем отладка последовательной программы, то системы отладки и профилирования являются важнейшей частью в процессе разработки таких систем. В области отладчиков хочется обратить внимание на системы TotalView и PGDBG. Среди средств профилирования можно назвать такие инструменты как Nupshot, Pablo, Vampir. Существуют системы статической верификации, например VivaMP. Последней инструмент, на который хочется обратить особое внимание, является средства анализа многопоточности Threading Analysis Tools. Но самый важный компонент, без которого все другие средства не смогут сделать программу параллельной, это параллельный алгоритм. Именно этому компоненту и будет посвящена эта работа. В работе будут рассмотрены несколько базовых параллельных алгоритмов, имеющих практическое значение во многих областях, в том числе в экономике, в численном моделировании и в задачах реального времени. Для некоторых алгоритмов приведены оценки времени выполнения последовательной и параллельной версий алгоритма и выведены коэффициенты ускорения. Приведен пример реализации описанных алгоритмов c использованием языка программирования Си++ в среде Windows.
Параллельная сортировка Бэтчера
Параллельная сортировка Бэтчера.Если мы хотим получить алгоритм обменной сортировки, время работы которого имеет порядок, меньший N2, то необходимо подбирать для сравнений некоторые пары несоседних ключей (Ki, Kj); иначе придется выполнить столько обменов, сколько инверсий имеется в исходной перестановке, а среднее число инверсий равно (N2 - N)/4. В 1964 г. К. Э. Бэтчер [Proc. AFIPS Spring Joint Computer Conference, 32 (1968), 307—314] открыл один искусный способ запрограммировать последовательность сравнений, предназначенную для отыскания возможных обменов. Его метод далеко не очевиден. В самом деле, только для того, чтобы показать его справедливость, требуется весьма сложное доказательство, так как выполняется относительно мало сравнений
Таблица 1 Обменная сортировка со слиянием (метод Бэтчера)
Схема сортировки Бэтчера несколько напоминает сортировку Шелла, но сравнения выполняются по-новому, так что распространение обменов не обязательно. Так, можно сравнить табл. 1 с аналогичной таблицей сортировки по методу Шелла. Сортировка Бэтчера действует как 8-сортировка, 4-сортировка, 2-сортировка и 1-сортировка, но сравнения не перекрываются. Так как в алгоритме Бэтчера, по существу, происходит слияние пар отсортированных подпоследовательностей, то его можно назвать "обменной сортировкой со слиянием".
Рис. 1. Блок-схема алгоритма сортировки со слиянием. Алгоритм М.(Обменная сортировка со слиянием.) Записи R1, ..., RN переразмещаются на том же месте. После завершения сортировки их ключи будут упорядочены: K1 ≤ ... ≤ КN -предполагается, что N > 2. Ml. [Начальная установка р.] Установить p← 2t-1, где — наименьшее целое число, такое, что 2 t = N. (Шаги М2, .. ., М5будут выполняться с р = 2t-l, 2t-2, ..., 1) М2. [Начальная установка q,r,d.]Установить q←2t-l, r←0, d←p. МЗ. [Цикл по i.] Для всех t, таких, что 0 ≤ i < N - d и rpi=∧, выполнить шаг М4. Затем перейти к шагу М5. (Здесь через i∧p обозначена операция "логическое и" над двоичными представлениями чисел i и р; все биты результата равны 0, кроме тех, для которых в соответствующих позициях i и р находятся единичные биты. Так, 13^21=(1101)2^(10101)2=(00101)2=5. К этому моменту d— нечетное кратное р (т. е. 'частное от деления d на р нечетно), а р — степень двойки, так что i^p≠(i+d)^p; отсюда следует, что действия шага М4можно выполнять при всех нужных значениях i в любом порядке или даже одновременно.) М4. [Сравнение/обмен Ri+1, Ri+d+1] Если Ki+1 > Ki+d+1, то поменять местами Ri+1 ↔ Ri+d+1 М5.[Цикл по q.] Если q ≠ р, то установить d ← q - p, q ← q/2, r ← р и возвратиться к шагу МЗ. М6.[Цикл по р.] (К этому моменту перестановка K1, К2, ..., КN будет p - упорядочена.) Установить p←(p/2) (целая часть). Если р > 0, то возвратиться к шагу М2. В табл. 1 этот метод проиллюстрирован при N = 16. Заметим, что алгоритм сортирует N элементов, по существу, путем независимой сортировки подфайлов R1, R3, R5,... и R2, R4, R6,..., после чего выполняются шаги М2, ..., М5 с р = 1, чтобы слить две отсортированные последовательности. Чтобы доказать, что магическая последовательность сравнений и/или обменов, описанная в алгоритме М, действительно позволяет рассортировать любую последовательность R1, R2, ..., RN, необходимо показать только, что в результате выполнения шагов М2-М5при р = 1 будет слита любая 2-упорядоченная последовательность R1, R2, ..., RN. С этой целью можно воспользоваться методом решеточных диаграмм; каждая 2-упорядоченная перестановка множества {1, 2, ..., N} соответствует на решетке единственному пути из вершины (0,0) к ((N/2,(N/2)) . На рис. 2, (а) показан пример при N = 16, соответствующий перестановке 1 3 2 4 10 5 11 6 13 7 14 8 15 9 16 12. При р = 1, q = 2t-1, r = 0, d = 1 на шаге МЗвыполняется сравнение (и, возможно, обмен) записей R1 : R2, R3 : R4 и т. д. Этой операции соответствует простое преобразование пути на решетке: "перегиб" относительно диагонали при необходимости, чтобы путь нигде не проходил выше диагонали (рис. 2, (b)). На следующей
Рис. 2. Геометрическая интерпретация метода Бетчера (N=16). итерации шага М3имеем р = r = 1иd= 2t-1-1, 2t-2-1, …, 1. В результате произойдет сравнение и/или обмен записей R2 : R2+d, R4 : R4+d и т.д. Опять же, имеется простая геометрическая интерпретация: путь "перегибается" относительно прямой, расположенной на 1/2(d+1) единиц ниже диагонали (рис. 2, (с) и (d)). В конце концов, получаем путь, изображенный на рис. 2, (е), который соответствует полностью рассортированной перестановке. На этом "геометрическое доказательство" справедливости алгоритма Бэтчера завершается (данный алгоритм можно было бы назвать сортировкой посредством перегибов!). К сожалению, количество вспомогательных операций, необходимых для управления последовательностью сравнений, весьма велико, так что Алгоритм М менее эффективен, чем другие рассмотренные выше методы. Однако он обладает одним важным компенсирующим качеством: все сравнения и/или обмены, определяемые данной итерацией шага МЗ, можно выполнять одновременно на компьютерах или в сетях, которые реализуют параллельные вычисления. Например, 1 024 элемента можно рассортировать методом Бэтчера всего за 55 параллельных шагов. Его ближайшим соперником является метод Пратта, который затрачивает 40 или 73 шага в зависимости от того, как считать: если допускать перекрытие сравнений до тех пор, пока не потребуется выполнять перекрывающиеся обмены, то для сортировки 1 024 элементов методом Пратта требуется всего 40 циклов сравнения и/или обмен. Алгоритм сортировки Бэтчера не является наиболее эффективным алгоритмом сортировки, однако он обладает одним важным компенсирующим качеством: все сравнения и/или обмены, определяемые данной итерацией алгоритма можно выполнять одновременно. С такими параллельными операциями сортировка осуществляется за Алгоритм Бэтчера (обменная сортировка со слиянием). Записи 1)[начальная установка
2)[начальная установка
3)[цикл по
Затем перейти к шагу 5. (Здесь через
4)[Сравнение/обмен
5)[Цикл по
6)[Цикл по //////////////////////////////////////// // Параллельная сортировка Бэтчера #include <stdio.h> #include <stdlib.h> #define N 16 int Arr[N]; void FillArray() { for (unsigned i = 0; i < N; i++) Arr[i] = rand() % 10; } void PrintArray() { for (unsigned i = 0; i < N; i++) printf("%d ", Arr[i]); printf("\n"); } void BatcherSort() { unsigned p = N; while (p > 0) { unsigned q = N, r = 0, d = p; bool b; do { unsigned nTo = N - d; for (unsigned i = 0; i < nTo; i++) if ((i & p) == r) { if (Arr[i] > Arr[i + d]) { int temp = Arr[i]; Arr[i] = Arr[i + d]; Arr[i + d] = temp; } } b = q != p; if (b) { d = q - p; q >>= 1; r = p; } } while (b); p >>= 1; } } int main(int argc, char* argv[]) { FillArray(); PrintArray(); BatcherSort(); PrintArray(); return 0; }
Умножение матриц
Задача умножения матриц является базовой макрооперацией для многих задач линейной алгебры. Поэтому эффективный параллельный алгоритм умножения матриц позволяет значительно увеличить размерность подобных задач без увеличения времени их решения. Пусть даны две матрицы,
Оценим время выполнения последовательного алгоритма. Пусть
Обозначим
Рассмотрим параллельный алгоритм умножения матриц и оценим время его работы.
Пусть имеется
Обозначим
Рассмотрим один из способов распараллеливания алгоритма. Пронумеруем элементы результирующей матрицы по следующему правилу (нумерация элементов, а также строк и столбцов в данном случае ведётся с нуля):
Вычисления распределим так, чтобы первый процессор вычислял первые
Рисунок 4. Схема распределения работ при параллельном умножении матриц.
Рассмотрим случай, когда //////////////////////////////////////// // Параллельное умножение матриц #include "windows.h" #include "process.h" #include "stdio.h" #include "assert.h" #define M 3 #define N 4 #define NumberOfProcessors 3 int A[M][N]; int B[N][M]; int C[M][M]; void InititalizeMatices() { unsigned i, j, n; printf("\nMatrix A:\n"); for (i = 0, n = 1; i < M; i++) { for (j = 0; j < N; j++, n++) { A[i][j] = n; printf("%4d ", n); } printf("\n"); } printf("\nMatrix B:\n"); for (i = 0, n = 1; i < N; i++) { for (j = 0; j < M; j++, n++) { B[i][j] = n; printf("%4d ", n); } printf("\n"); } } unsigned __stdcall ThreadFunction(void *pData) { unsigned Branch = (unsigned)pData; unsigned Start = M / NumberOfProcessors * Branch; unsigned End = M / NumberOfProcessors * (Branch + 1); for (unsigned i = Start; i < End; i++) for (unsigned j = 0; j < M; j++) { int Value = A[i][0] * B[0][j]; for (unsigned k = 1; k < N; k++) Value += A[i][k] * B[k][j]; C[i][j] = Value; } return 0; } int main(int argc, char* argv[]) { UNREFERENCED_PARAMETER(argc); UNREFERENCED_PARAMETER(argv); assert(M % NumberOfProcessors == 0); InititalizeMatices(); HANDLE hThreads[NumberOfProcessors]; unsigned i, j, n, tid; for (i = 0; i < NumberOfProcessors; i++) hThreads[i] = (HANDLE)_beginthreadex(NULL, 0, ThreadFunction, (void *)i, 0, &tid); WaitForMultipleObjects(NumberOfProcessors, hThreads, TRUE, INFINITE); for (i = 0; i < NumberOfProcessors; i++) CloseHandle(hThreads[i]); printf("\nMatrix C = A * B:\n"); for (i = 0, n = 1; i < M; i++) { for (j = 0; j < M; j++, n++) printf("%4d ", C[i][j]); printf("\n"); } return 0; } Заключение В работе были рассмотрены несколько базовых параллельных алгоритмов, имеющих практическое значение во многих областях, в том числе в экономике, в численном моделировании и в задачах реального времени. Приведен пример реализации описанных алгоритмов c использованием языка программирования Си++ . Надеюсь, работа поможет немного лучше разобраться в вопросах параллельного программирования, а приведенные примеры наглядно продемонстрировали некоторые параллельные алгоритмы. Литература Элементы параллельного программирования / В.А. Вальковский, В.Е. Котов, А.Г. Марчук, Н.Н. Миренков; под ред. В.Е. Котова. — М.: Радио и связь, 1983. — 240с.,интеграл. Алгоритмы, математическое обеспечение и архитектура многопроцессорных вычислительных систем / Под ред. В.Е. Котова и И. Миклошко — М.: Наука, 1982. — 336 с. Миренков Н.Н. Параллельное программирование для многомодульных вычислительных систем. — М.: Радио и связь, 1989. — 320с.: ил. — ISBN 5-256-00196-5 Шихаев К.Н. Разностные алгоритмы параллельных вычислительных процессов. — М.: Радио и связь, 1982. — 136с., ил. Вальковский В.А. Распараллеливание алгоритмов и программ. Структурный подход. М.: Радио и связь, 1989. —176с., ил. — ISBN 5-256-00195-7.
|







 .
. перекомпоновываются в пределах того же пространства в памяти. После завершения сортировки их ключи будут упорядочены
перекомпоновываются в пределах того же пространства в памяти. После завершения сортировки их ключи будут упорядочены  . Предполагается, что
. Предполагается, что 
 .] Установить,
.] Установить,  , где
, где 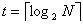 — наименьшее целое число, такое, что
— наименьшее целое число, такое, что  . (Шаги 2-5 будут выполняться с
. (Шаги 2-5 будут выполняться с  .)
.) .] Установить
.] Установить  .
. .] Для всех
.] Для всех  , таких, что
, таких, что  и
и  , выполнять шаг 4.
, выполнять шаг 4.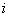 и
и  . К этому моменту
. К этому моменту  — нечётное кратное
— нечётное кратное  . Отсюда следует, что шаг 4 можно выполнять при всех нужных значениях в любом порядке или даже одновременно.)
. Отсюда следует, что шаг 4 можно выполнять при всех нужных значениях в любом порядке или даже одновременно.)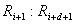 .] Если
.] Если  , поменять местами записи
, поменять местами записи  .
. .] Если
.] Если  , установить
, установить 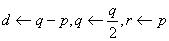 и возвратиться к шагу 3.
и возвратиться к шагу 3. будет
будет  . Если
. Если  , возвратиться к шагу 2.
, возвратиться к шагу 2. и
и  ., произведение которых необходимо вычислить. Элементы результирующей матрицы
., произведение которых необходимо вычислить. Элементы результирующей матрицы  определяются по формуле
определяются по формуле
 — время, затрачиваемое на умножение двух чисел,
— время, затрачиваемое на умножение двух чисел,  — время сложения двух чисел. Время, затрачиваемое на вычисление одного элемента результирующей матрицы
— время сложения двух чисел. Время, затрачиваемое на вычисление одного элемента результирующей матрицы  . В результирующей матрице содержится
. В результирующей матрице содержится  элементов, поэтому общее время выполнения умножения матриц равно
элементов, поэтому общее время выполнения умножения матриц равно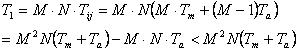
 Отсюда следует, что
Отсюда следует, что  .
. процессоров, причём,
процессоров, причём,  ,
,  где — целое. Распараллелим вычисления так, чтобы каждый процессор вычислял
где — целое. Распараллелим вычисления так, чтобы каждый процессор вычислял  элементов результирующей матрицы. Тогда суммарное время выполнения можно оценить следующим образом:
элементов результирующей матрицы. Тогда суммарное время выполнения можно оценить следующим образом:
 Сравнивая
Сравнивая  и
и  , получим:
, получим:  Имеем, что время, затрачиваемое на умножение матриц с помощью параллельного алгоритма, в
Имеем, что время, затрачиваемое на умножение матриц с помощью параллельного алгоритма, в  раз меньше, чем при использовании последовательного.
раз меньше, чем при использовании последовательного.

 (количество процессоров больше, чем элементов в результирующей матрице). Незадействованные
(количество процессоров больше, чем элементов в результирующей матрице). Незадействованные  процессоров можно использовать для ускорения вычисления отдельных элементов результирующей матрицы. При этом следует использовать способ распараллеливания, подобный использованному при вычислении скалярного произведения векторов.
процессоров можно использовать для ускорения вычисления отдельных элементов результирующей матрицы. При этом следует использовать способ распараллеливания, подобный использованному при вычислении скалярного произведения векторов.