 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ТЕХНИЧЕСКАЯ И МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ РАСЧЕТА УСТАНОВИВШЕГОСЯ РЕЖИМА
Расчеты установившихся режимов составляют существенную часть общего объема исследований электроэнергетических систем, выполняемых на стадии проектирования и в процессе эксплуатации. В качестве необходимого информационного обеспечения их результаты используются: 1 – при выборе конфигурации схемы электрической системы; 2 – при выборе параметров элементов схемы; 3 – при анализе устойчивости; 4 – при определении наиболее экономичных режимов работы системы. Расчеты установившихся режимов позволяют ответить на ряд практически важных вопросов, определяющих их самостоятельную ценность: 1 – осуществимость данного режима, то есть определение возможности передачи требуемой мощности от источников электроэнергии к потребителям; 2 – не превышение токами нормального и послеаварийного режимов предельно допустимых для элементов значений; 3 – нахождение диапазона изменения напряжений в узловых точках в пределах допустимого. В качестве исходной информации для расчета установившихся режимов необходимы данные: 1) о схеме и параметрах сети электрической системы; 2) о потребителях (нагрузках); 3) об источниках энергии (электростанциях). Как известно, сеть электрической системы в расчетах установившихся режимов представляется схемой замещения в виде линейной электрической цепи, конфигурация и параметры которой отражаются той или иной матрицей обобщенных параметров. Исходными данными о нагрузках реальных электрических систем при их проектировании и эксплуатации обычно служат значения потребляемых ими активных и реактивных мощностей,
которые могут приниматься постоянными:
либо зависящими от напряжения в точке подключения нагрузки к сети:
(учет статических характеристик нагрузки по напряжению). Исходными данными об источниках питания, как правило, служат выдаваемые генераторами в систему активные мощности
и абсолютные значения напряжений в точках их подключения:
хотя в ряде случаев источники питания могут быть заданы и постоянными значениями активных и реактивных мощностей
аналогично нагрузкам. Кроме того, один из источников, как правило наиболее мощная электростанция, играющий роль балансирующего, задается комплексным значением напряжения:
При указанных исходных данных целью расчета установившегося режима электрической системы в общем случае является определение:
1) – мощностей и токов в ветвях схемы замещения; 2) - комплексных значений напряжения в ее узловых точках.
С математической точки зрения задача сводится к решению системы нелинейных уравнений из-за нелинейной зависимости мощности от тока и напряжения. Конкретный вид этих уравнений определяется формами уравнений состояния, положенных в основу математического описания установившегося режима, и обобщенными параметрами системы. Из уравнений состояния наиболее широко применяются узловые уравнения, которые характеризуются как простотой формирования, так и большими возможностями эффективной организации процесса их решения. Контурные уравнения формируются несколько сложнее, имеют принципиально неустранимые ограничения, однако и они имеют определенную рациональную область применения. В основу дальнейшего рассмотрения положим систему узловых уравнений, имея в виду, что идентичность структур матричных узловых и контурных уравнений, а также подобие свойств матриц узловых проводимостей и контурных сопротивлений предопределяет возможность использования для их решения одних и тех же методов. Уравнения установившегося режима электрической системы трехфазного переменного тока, связывающие токи и напряжения узлов при отсутствии ЭДС в ветвях имеют вид:
Важно отметить, что в уравнении (2-1) мощность трехфазной цепи определяется фазными значениями напряжений и токов. В расчетах установившихся режимов электрических систем обычно используется выражение мощности через линейные напряжения и фазные токи, при этом уравнения приобретают вид
И второе замечание: два комплексных числа
Система нелинейных (2-1) и линейных (2-2) уравнений при заданных мощностях узлов в общем случае может быть решена только итерационным методом. При этом возможны два подхода к решению: - поочередное решение уравнений (2-1) и (2-2) в общем итерационном цикле; - объединение этих уравнений в единую систему нелинейных уравнений и последующее ее решение.
В первом случае решение проводится по следующей схеме: 1) Задаются начальными приближениями напряжений узлов, что более удобно, чем задание токов в узлах, поскольку в реальных условиях фактические напряжения в узлах незначительно отличаются от номинальных значений; 2) По значениям напряжений и заданным значениям мощностей из 3) Решается система линейных уравнений (2-2) при известных значениях задающих токов относительно напряжений в узлах; 4) На основе полученных значений напряжений в узлах выполняется следующий цикл итерационного процесса, начиная с шага 2. Условием окончания итерационного процесса является достаточно близкое с инженерной точки зрения совпадение напряжений на двух последующих итерациях, а также совпадение вычисленных по выражению (2-1) значений мощностей узлов с заданными. Во втором случае уравнения (2-1) и (2-2) объединяются: либо уравнение (2-1) заменяем на сопряженное и подставляем в него(2-2):
либо величины из сопряженного (2-1) подставляем в (2-2):
Системы нелинейных уравнений (2-3) и (2-4) решаются итерационными методами относительно напряжений в узлах. Применяемые в практике расчетов установившихся режимов методы решения этих уравнений основаны на их линеаризации на каждом шаге итерационного процесса.
Таким образом, как при первом, так и при втором подходе на каждом шаге итерационного процесса необходимо решать систему линейных алгебраических уравнений либо непосредственно в виде узловых уравнений
Факторами, определяющими эффективность процесса расчета установившегося режима на ЭВМ являются: 1 – надежность вычислительного процесса – построение алгоритмов, исключающее появление чрезмерно больших погрешностей при решении задачи прямыми методами и обеспечивающее быструю сходимость при решении задачи итерационными методами; 2 – экономное использование памяти ЭВМ и сокращение времени вычислений за счёт рационального (компактного) представления исходных данных о системе с учётом её структурных свойств; 3 – гибкость алгоритма и программы, т.е. возможность различной степени детализации представления любой части электрической системы и легкость учета изменений расчетной схемы замещения системы в зависимости от целей исследований.
Необходимым условием реализации вычислительного процесса на ЭВМ является получение результатов с достаточной для инженерных целей точностью, критерии оценки которой и численные показатели определяются технической постановкой задачи. Обеспечение надёжной и экономичной работы сложных энергообъединений требует создания автоматизированных систем диспетчерского управления, функционирование которых связано с необходимостью многократного оперативного выполнения расчетов установившихся режимов. Поэтому, несмотря на увеличение возможностей ЭВМ, факторы экономного использования памяти и сокращения времени вычислений становятся всё более важными. В данных условиях разработка эффективных алгоритмов расчетов установившихся режимов требует максимального учета всех специфических особенностей, которыми характеризуются схемы замещения реальных электрических систем и соответствующие им матрицы обобщённых параметров. Эти особенности необходимо учитывать как при формировании уравнений установившегося режима, так и при выборе наиболее рационального метода их решения и, прежде всего рассматриваемых далее методов решения систем линейных алгебраических уравнений.
|



 ,
, ,
,
 ,
, ,
,
 .
.
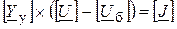 , где
, где - столбец мощностей источников или потребителей, присоединенных к узлам схемы замещения системы;
- столбец мощностей источников или потребителей, присоединенных к узлам схемы замещения системы; - диагональная матрица напряжений в узлах схемы замещения;
- диагональная матрица напряжений в узлах схемы замещения; - столбец напряжений в узлах схемы;
- столбец напряжений в узлах схемы; - столбец, каждый элемент которого равен напряжению в балансирующем узле
- столбец, каждый элемент которого равен напряжению в балансирующем узле  ;
; - столбец задающих токов в узлах (символом
- столбец задающих токов в узлах (символом  отмечаются комплексно-сопряженные величины).
отмечаются комплексно-сопряженные величины). ;
;
 и
и  называются сопряженными. Использование сопряженного комплекса тока для определения комплекса мощности рассматривается в курсе ТОЭ.
называются сопряженными. Использование сопряженного комплекса тока для определения комплекса мощности рассматривается в курсе ТОЭ. ;
;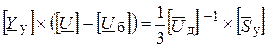 .
.