 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Примерные (типовые) задачи, выносимые на экзамен
НИЖЕГОРОДСКОЕ ВЫСШЕЕ ВОЕННО-ИНЖЕНЕРНОЕ КОМАНДНОЕ УЧИЛИЩЕ Кафедра электроснабжения Экз. №__
ПРОГРАММНЫЕ ВОПРОСЫ Для подготовки студентов к Устному экзамену по учебной дисциплине «Надежность электроснабжения»
Кстово – 2010 НИЖЕГОРОДСКОЕ ВЫСШЕЕ ВОЕННО-ИНЖЕНЕРНОЕ КОМАНДНОЕ УЧИЛИЩЕ Кафедра электроснабжения Экз. №__
УТВЕРЖДАЮ ВРИО заместителя начальника училища по учебной и научной работе полковник А.Н. ЯНЮК «___» ___________ 2010 г.
Студенты Специальность – В ПРОГРАММНЫЕ ВОПРОСЫ Для подготовки студентов к Устному экзамену по учебной дисциплине «Надежность электроснабжения»
Обсуждены на заседании ПМК кафедры Протокол № ___ от «___»_________2010 г.
Кстово - 2010 1. Теоретические вопросы для подготовки к экзамену 1. Основные термины и определения теории надежности. 2. Основные задачи теории надежности. 3. Основные понятия теории вероятности. 4. Теоремы сложения, умножения и полной вероятности. 5. Случайные величины, их числовые характеристики, функция и плотность распределения 6. Потоки отказов и восстановлений. 7. Количественная оценка показателей надежности 8. Сбор информации об отказах элементов технических систем. 9. Состав информации. 10. Проверка однородности статистического материала. 11. Проверка гипотез о законе распределения случайной величины. 12. Точность оценки. Доверительная вероятность. Доверительный интервал. 13. Контроль показателей качества и надежности. 14. Модели отказов электроустановок. 15. Модели надежности установок с восстановлением 16. Моделирование надежности электроустановок с восстановлением. 17. Моделирование надежности электроустановок с восстановлением и профилактикой. 18. Аналитический метод расчета надежности электроустановок. 19. Логико-вероятный метод расчета надежности электроустановок. 20. Таблично-логический метод расчета надежности электроустановок. 21. Метод имитационного моделирования 22. Общие принципы определения ущерба от нарушений электроснабжения. 23. Оценка ущерба методами макромоделирования. 24. Модель проведения участка производства при нарушениях его электроснабжения. 25. Технико-экономическая оценка последствий нарушений нормального режима электроснабжения объектов производственных систем. 26. Предпосылки к разработке к разработке нормативов надежности электроснабжения промышленных потребителей. 27. Принципы нормирования и рекомендации по составу нормативов надежности электроснабжения потребителей. 28. Методический подход к исследованию и уточнению предельных нормативов надежности электроснабжения. 29. Анализ живучести производственных систем в задачах электроснабжения. 30. Методы выделения особо ответственных электроприемников и нормативные требования к их надежности. 31. Экономико-организационные проблемы разгрузки предприятий при дефиците мощности и прохождении максумумов нагрузки в энергосистеме. 32. Основы принятия решений по ограничению потребителей при дефицитах мощности в ЭЭС. 33. Учет технологических резервов предприятий при управлении режимами электропотребления. 34Экономическая оценка эффективности управления электропотреблением. 35. Задачи обследования промышленных объектов при управлении нагрузкой. 36. Необходимость использования экспертных оценок.
37. Основные положения и особенности экспертного оценивания показателей последствий управления нагрузкой. 38. Оценка вероятностей возможных последствий от нарушений электроснабжения потребителей.
Примерные (типовые) задачи, выносимые на экзамен
1. В распределительном пункте (РП) установлено пять автоматических выключателей. Нормальная работа потребителей обеспечивается при их исправном состоянии. При монтаже РП выбирались из партии объемом в 1000 штук, в которой било 950 исправных выключателей и 50 неисправных. Найти вероятность исправной работы РП 2. Вероятность выхода из строя электрического прибора равна Р = 0,01. Для повышение надежности в прибор поставлены m дублирующих ветвей. Определить, во сколько раз (k) увеличится надежность прибора, если под ней понимать вероятность безотказной работы. 3. Две цепи электроснабжения работают параллельно на общую нагрузку.
Рисунок - Схема питания
Вероятность аварийного простоя одной цепи а) отказ электропередачи происходит при отказе оной из цепей (любой); б) отказ электропередачи происходит при отказе только обеих цепей.
4. Питание потребителя осуществляется по одной цепи, состоящей из кабельной линии, трансформатора, выключателя.
Рисунок- Схема питания Вероятность безотказной работы за время t для этих элементов: Ркл = 0,7, Рт = 0,8, Рв = 0,9. Отказ любого элемента приводит к перерыву питания, причем отказы взаимно независимы. Найти вероятность безотказной работы передачи.
5. Питание потребителя осуществляется по одной цепи, состоящей из кабельной линии, трансформатора, выключателя.
Рисунок- Схема питания Вероятность безотказной работы за время t для этих элементов: Ркл = 0,7, Рт = 0,8, Рв = 0,9. Отказ любого элемента приводит к перерыву питания, причем отказы взаимно независимы. Найти вероятность отказа передачи.
6. Силовые трансформаторы изготавливаются тремя заводами, причём вероятность того, что трансформатор выпущен на первом заводе, равна 0,2, на втором – 0,3, на третьем — 0,5. Вероятность того, что при определенных условиях работы трансформатор сохранит работоспособность в течение 25 лет, для первого, второго и турьего заводов соответственно равны: 0,9; 0,92; 0,808. Чему равна вероятность того, что поступивший для монтажа трансформатор сохранит работоспособность в течение 25 лет? 7. Пропускная способность канала связи в система телемеханики зависит от появления ошибки внутри канала (рисунок 2.3) На вход канала могут подаваться два сигнала х1 и х2. На выходе принимаются соответственно y1и y2.40% времени канал занят передачей сигнала х1 и 60% времени — сигнала х2. Вероятность безошибочной передачи сигнала х1 как у1 равна 0,75. Вероятность того, что входной сигнал х1 будет ошибочно принят как у2, равна 0,25. Аналогично вероятность того, что сигнал, первоначально переданный как х2 будет принят как у2 и у1, равна соответственно 0,9 и 0,1. При заданных условиях получен выходной сигнал у1. Какова вероятность того, что исходный сигнал был х1?
Рисунок – Схема канала связи
8. Энергосистема ограничивает военный объект в потреблении энергетической мощности. При этом в течение года возможны дефициты в 5, 10 и 15 МВт с вероятностями соответственно 0,001. 0.0004 и 0,0002. Определить математическое ожидание недоотпуска электроэнергии военному объекту за год.
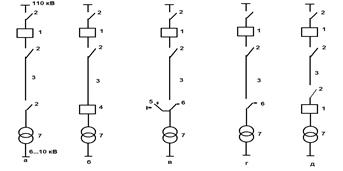
9. В результате испытания 36 образцов аппаратуры была зафиксирована 231 неисправность. При этом каждый из испытуемых образцов проработал в среднем по 19 часов. Определить среднюю наработку на отказ. 10. Имеется восстанавливаемая система, у которой параметр потока отказов l = 11. Восстанавливаемая система состоит из трех последовательно включенных элементов с параметрами надежности: Определить коэффициент надежности. 12.Рассмотрим блочные схемы питания однотрансформаторных подстанций 110 кВ (рисунок 1.1). Отказ СЭС таких подстанций вызывается отказом любого из элементов системы. Частота отказов этих элементов приведена ниже:
Рисунок – Схемы питания однотрансформаторных подстанций 13. Рассмотрим схему секции РУ-6 кВ. от которой питается 21 отходящая линия. Частота отказов с короткими замыканиями для выключателей оценивается величиной λв =0.003 1/год, а частота отказов с коротким замыканием для сборных шин λш =0.03 1/год. 14. Потребители питаются от двух независимых источников. Один источник включен постоянно, второй включается действием АВР (рисунок 1.2). Вероятность безотказной работы источников в течение расчетного периода времени равна Р(И1)=0,99.Вероятность застать резервный источник в работоспособном состоянии в любой момент времени Р(И2)=0,99. Вероятность отказа в отключении Q(A1)=0,05,во включении Q(A2)=0,01. определить вероятность безотказной работы СЭС в течение расчетного времени с учетом возможности использования резервного источника, считая, что вероятность отказа резервного источника за время восстановления рабочего можно пренебречь.
Рисунок – Схема питания
15. Рассмотрим элемент с равномерным распределением элементов в конце периода Тпл составляет 75% числа работоспособных элементов в начале периода Тпл. 16. Рассмотрим элемент с равномерным распределением срока службы f(t) = ¼ 1/год при 0< t > 4 года и периодичности предупредительных ремонтов Тпл = 1 год. 17. Выпущена партия резисторов 100000 штук. Вероятность того, что резистор имеет брак, р = 0,0001. Найти вероятность того, что в партии ровно пять бракованных резисторов. 18. Определить вероятность того, что за 500 ч работы произойдет два отказа в сложном изделии, если известно, что интенсивность отказов λ = 1 ∙ 10-3. 19. Время безотказной работы силового трансформатора при перегрузке распределено по экспоненциальному закону f = 0,02e-0,02t , где t – время, ч. Найти вероятность того, что трансформатор в перегрузочном режиме проработает безотказно в течение 100 ч. 20. Наблюдения за эксплуатацией 10 электродвигателей выявили, что первый проработал до отказа 800 ч, второй – 1200 и далее соответственно 900, 1400, 700, 950, 750, 1300, 850 и 1500 ч. Определить наработку двигателей до внезапного отказа. 21. При эксплуатации 100 трансформаторов в течение 10 лет произошло два отказа, причем каждый раз отказывал новый трансформатор. Определить интенсивность отказов трансформатора за период наблюдения. 22. Изменение числа отказов ВЛ из-за производственной деятельности сторонних организаций по месяцам года представлено следующим образом:
Определить среднемесячную интенсивность отказов. 23. Трансформатор отказал, проработав около года. После устранения причины отказа он проработал еще три года и опять вышел из строя. Определить среднюю наработку трансформатора на отказ. 24. Электротехническое устройство состоит из трех элементов. В течение первого года эксплуатации в первом элементе произошло два отказа, во втором – один, в третьем отказов не было. Определить параметр потока отказов. 25. За год эксплуатации зарегистрирован m =21 случайных отказов воздушных выключателей и = 330 кВ при отключении ими коротких замыканий. Число эксплуатируемых выключателей в этом году составляло N = 1750 шт. Оценить средний параметр потока отказов и его доверительные границы с доверительной вероятностью β = 0,95. 26. Определить показатели надежности СЭС с двумя кабельными линиями 6 кВ: λ = 0,2 год-1; длительность восстановления t = 24 ч; t = 1 год. 27. Рассмотрим элемент с равномерным распределением срока службы f(t) = 1/4 год-1 при 0< t ≤ 4 года и периодичности предупредительных ремонтов Тпл = 1 год. 28. В течение пяти лет наблюдений (t = 5) из семи работающих на электростанции генераторов N0 = 7, отказало два N(t) = N(5) = 2. 29. При эксплуатации 70 сухих трансформаторов в течение 10 лет произошло пять отказов, причем каждый раз отказывал новый трансформатор. 30. Проверим гипотезу об экспоненциальном распределении длительности работы 200 ламп накаливания с помощью критерия хи-квадрат Пирсона. Результаты наблюдений представлены таблицей и гистограммой.
|
, второй 
. Принимая аварийные состояния цепей независимыми, определить вероятность аварийного простоя двухцепной электропередачи для двух случаев:
1/ч = const, средняя интенсивность восстановления 
1/ч. Определить, на сколько повысится надежность этой системы за счет более высокой организации работы ремонтного персонала, если интенсивность восстановления системы повысилась вдвое (сократилось вдвое время восстановления).
= 0,6; 
= 0,8; 
= 0,7. Известно, что 
.
