 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Построение жорданова базиса
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение Высшего профессионального образования Московский государственный институт электроники и математики (технический университет) Кафедра алгебры И математической логики
ПОСТРОЕНИЕ ЖОРДАНОВА БАЗИСА Методические указания К домашней контрольной работе По курсу линейной алгебры и аналитической геометрии Москва Составитель: канд. физ.-мат. наук К. К. Андреев
УДК 512.8
Построение жорданова базиса: Метод. указания к домашней контрольной работе по курсу линейной алгебры и аналитической геометрии./ Моск. гос. ин-т электроники и математики; Сост.: К. К. Андреев. М., 2009. – 25 с., 3 рис.
На конкретных примерах излагаются способы решения задач домашней контрольной работы по теме «Жорданов базис». Приводится ряд сведений из теории линейных операторов. Для студентов первого курса групп ЗИ, М, МЭ, ЭМ.
ISBN Условия задач
Общие условия ко всем вариантам В пространстве R8даны линейные операторы j и y, матрицы которых в стандартном базисе соответственно равны A и B. Для каждого линейного оператора найти какой-нибудь жорданов базис и жорданову форму, матрицу перехода от стандартного базиса к найденному жорданову. Проверить выполнение формулы, связывающей матрицы линейного оператора в разных базисах.
Условия вариантов
1. A = 2. A =
3. A =
4. A =
5. A =
6. A =
7. A =
8. A =
9. A =
10. A =
11. A =
12. A =
13. A =
14. A =
15. A =
16. A =
17. A =
18. A =
19. A =
20. A =
21. A =
22. A =
23. A =
24. A =
25. A =
26. A =
27. A =
28. A =
29. A =
30. A =
Построение жорданова базиса
Замечание. Алгорифм построения жорданова базиса я излагаю здесь, следуя лекциям проф. Ю. Ю. Кочеткова на ФПМ, читанным в 2005 году. Ему же принадлежат и варианты контрольной работы, из которых здесь разбирается вариант № 27. Пусть в пространстве Rn (Cn) дан линейный оператор j, для которого число λ Î R (C) является собственным значением. Рассмотрим подпространства Mi = Ker ((j − λe)i). Очевидно, что эти подпространства вложены друг в друга: Mi Í Mi+1. Размерности mi = dim Mi, следовательно, связаны соотношениями: mi £ mi+1. Так как размерности mi ограничены размерностью всего пространства n, то последовательность размерностей стабилизируется, т. е., начиная с некоторого номера, mk = mk+1. Пусть k − это наименьший номер такой, что mk = mk+1. Тогда: m1 < m2 < … < mk−1 < mk = mk+1 = mk+2 = … . Соответствующие соотношения выполняются и для самих подпространств: M1 < M2 < … < Mk−1 < Mk = Mk+1 = Mk+2 = … . Легко видеть, что подпространство Mk представляет собою не что иное, как совокупность всех тех и только тех векторов x пространства Rn (Cn), для которых существует такое s, что (j − λe)s(x) = 0. Это подпространство называется корневым подпространством оператора j, соответствующим данному собственному значению λ. Обозначим его Eλ. Оно, очевидно, содержит соответствующее собственное подпространство Vλ = M1. Можно доказать, что размерность корневого подпространства Eλ равна кратности собственного значения λ как корня характеристического уравнения. Подмножества Mi+1\Mi я называю слоями, а разность (mi+1 − mi) − толщиной соответствующего слоя. Условно можно положить M0 = {0}. Можно доказать, что последовательность толщин слоёв убывает в нестрогом смысле. Рассмотрим примеры. Пусть матрицей оператора j в стандартном базисе пространства R8 является матрица A = Поскольку эта матрица является верхнею треугольною, её диагональ представляет собою спектр; таким образом, спектр матрицы A (оператора j) есть S = {0[8]}. Матрицей оператора j2 будет матрица A2, оператора j3 − матрица A3 и т. д. Напомню, что вектор j(x), рассматриваемый как матрица-столбец, равен произведению матриц A и x: j(x) = Ax. Следовательно, для нахождения ядра оператора (j − λe)i = ji (λ = 0!) достаточно решить однородную систему линейных уравнений AiX = 0. Вычисляем: A2 = Очевидно, что rk A = 5, rk A2 = 3, rk A3 = 1, rk A4 = 0, так что m1 = dim M1 = 3, m2 = 5, m3 = 7, m4 = 8. В данном случае корневое подпространство E0 = M4 − это всё пространство R8. Толщины четырёх слоёв образуют нестрого убывающую последовательность 3, 2, 2, 1. Теперь найдём базисы подпространств M1, M2, M3, M4. Для этого приведём матрицы A, A2 и A3 к главному ступенчатому виду: A = A2 = A3 = Исходя из вида приведённых матриц, можно написать: M1 = á M3 = áe1, e2, …, e7ñ. В качестве базиса M4 = R8 можно взять стандартный базис e1, e2, …, e8. Приступаем к построению жорданова базиса. Начинаем с внешнего слоя M4\M3. Дополним базис M3 до базиса M4. В данном примере очевидно, что дополняющим вектором будет вектор e8. В общем случае для нахождения дополняющих векторов составляем матрицу, столбцы которой суть векторы базиса подпространства M3, а затем все векторы базиса подпространства M4 (т. е. стандартный базис R8) (обязательно именно в этом порядке), и приводим её к главному ступенчатому виду:
В нашем случае построенная матрица уже сама является главной ступенчатой. Вид главной ступенчатой матрицы показывает нам, что базис M3 можно дополнить до базиса M4 вектором e8. (Первые семь главных столбцов соответствуют базису подпространства M3, восьмой главный столбец соответствует вектору e8.) Итак, мы нашли векторы, количество которых равно толщине последнего слоя. Эти векторы образуют фрагмент будущего жорданова базиса (в нашем примере вектор единствен). Вообще жорданов базис будет иметь в каждом слое столько векторов, какова его толщина. Введём ещё одно определение. Пусть x − произвольный ненулевой вектор из корневого подпространства. Рассмотрим последовательность векторов: x, (j − λe)(x), (j − λe)2(x), (j − λe)3(x), … . Все члены этой последовательности, начиная с некоторого номера, равны нулю, что следует из определения корневого подпространства. Если из этой последовательности все нулевые векторы выбросить, то оставшуюся конечную последовательность будем называть серией, построенной отправляясь от (начиная с) вектора x. Длина этой конечной последовательности у нас всегда будет равна номеру слоя, в котором лежит наш вектор (в общем случае это не обязательно). Так вот, теперь мы должны построить, начиная с каждого из найденных векторов, соответствующую серию, что добавит нам векторов в будущий жорданов базис. В нашем конкретном примере строим серию, отправляясь от единственного вектора e8: e8, j(e8) = Ae8 = (Кстати, вместо умножения A2 на e8 можно умножить матрицу A на уже найденный вектор Ae8 и т. д.)
Рис. 1
Мы построили уже четыре вектора будущего жорданова базиса − по одному в каждом слое. Теперь переходим к следующему слою (с меньшим номером). Если в следующем слое число уже построенных векторов равно толщине этого слоя (такой слой я называю насыщенным), то переходим к следующему слою (с ещё меньшим номером) и т. д. В нашем примере третий слой является ненасыщенным (его толщина равна двум, а уже построенных в нём векторов жорданова базиса один). Теперь мы должны построить такой базис подпространства M3, который содержит найденный выше базис подпространства M2, а также вектор j(e8). Чтобы этого добиться, строим матрицу, столбцы которой (именно в этом порядке) суть: базис M2, вектор j(e8), базис M3, и приводим её к главному ступенчатому виду:
® Последние семь столбцов ступенчатой матрицы содержат только один главный столбец − третий (из них). Он соответствует (в исходной построенной матрице) вектору e3. Значит, именно этот вектор надо добавить до базиса M3, и он войдёт в будущий жорданов базис. Теперь от него строим серию: e3, j(e3) = Ae3 = Эти векторы входят в строящийся жорданов базис. Мы уже построили семь векторов жорданова базиса (из восьми). У нас уже все слои стали насыщенными, кроме самого внутреннего (M1). Чтобы насытить его, строим матрицу, первыми двумя столбцами которой являются уже построенные векторы этого слоя j3(e8) = A3e8 =
Вид главной ступенчатой матрицы показывает нам, что добавить надо вектор Жорданов базис построен. Его векторы надо писать в определённом порядке: векторы одной серии надо писать подряд, но в порядке, обратном построению, начиная с бóльших степеней оператора. Серии между собой можно в принципе переставлять местами, но условимся для определённости (и для облегчения проверки работы преподавателем) писать серии в порядке их построения. В нашем случае получаем последовательность: j3(e8) = e3, Эти восемь векторов, записанные именно в этом порядке, и являются искомым жордановым базисом. Чтобы записать теперь матрицу перехода от исходного стандартного базиса к построенному жорданову, достаточно эти восемь векторов записать в виде столбцов квадратной матрицы (в том же порядке): T = Теперь нам надо записать вид получающейся жордановой матрицы, т. е. матрицы нашего оператора в построенном жордановом базисе. Для этого надо иметь в виду, что каждой построенной серии соответствует одна жорданова клетка, размер которой равен длине серии. В нашем случае длины серий равны 4, 3, 1 (берем серии обязательно в том порядке, как они выше записаны в базис!). Следовательно, жорданова матрица имеет вид: J = Наконец, для контроля наших вычислений проверим выполнение формулы J = T −1AT, которая, как мы знаем, равносильна формуле TJ = AT. Вычисляя, получаем для обеих матриц: TJ = AT = Рассмотрим теперь второй пример, где линейный оператор задаётся матрицею B = Диагональ этой треугольной матрицы представляет собою спектр S = {0[4]; 1[4]}. Теперь построение подпространств Mi придётся делать отдельно для каждого λ. Начнём с λ = 0. Здесь также надо возводить матрицу в степени, но надо ждать не когда они обнулятся (этого никогда не произойдёт), а когда обнулится левый верхний квадрат размера 4 на 4. B = B2= Вычисления прекращаем, т. к. обнулился левый верхний квадрат размера 4 на 4. Количества свободных неизвестных в приведённых матрицах показывают нам размерности подпространств. Таким образом, m1 = 2, m2 = m3 = … = 4. У нас всего два подпространства − M1 и M2, причём M2 является корневым подпространством. Ищем базисы этих подпространств: базис M1: e1,
Таким образом, дополняют базис M1 до базиса M2 векторы e2 и e4. Строим от них серии: y(e2) = Be2 = e1; y(e4) = Be4 =
Рис. 2
Значит, часть жорданова базиса, соответствующая λ = 0, такова: e1, e2, Остаётся рассмотреть λ = 1. В этом случае оператору y − λe = y − e соответствует матрица B − E = Подпространство M1 одномерно, его базис состоит из одного вектора u = (B − E)2 = (B − E)3 = (B − E)4 = Вычисления прекращаем, как только обнулится правый нижний квадрат размера 4 на 4. У нас это произошло на четвёртой степени. По количеству свободных неизвестных приведенных матриц определяем размерности подпространств M1, M2, M3, M4: m1 = 1, m2 = 2, m3 = 3, m4 = 4. Следовательно, у нас все четыре слоя имеют толщину 1. Значит, когда мы найдем вектор жорданова базиса в последнем слое и построим от него серию, мы получим уже все векторы жорданова базиса (для λ = 1). Для нахождения вектора строим базисы подпространств M3 и M4: базис M3: базис M4: Ясно (и без составления большой матрицы), что добавить надо вектор v. Таким образом, получаем серию: v, (y − e)(v) = (B − E)v =
Рис. 3
Соединяя с предыдущей серией (и записывая векторы каждой серии в обратном порядке), получаем жорданов базис: e1, e2, y(e4), e4,(y − e)3(v), (y − e)2(v), (y − e)(v), v. Этому жорданову базису соответствует матрица перехода: T = Жорданова форма: J = TJ = BT = Задача решена. Замечания. 1. Не следует торопиться с приведением степеней матриц к главному ступенчатому виду. Так, в последнем примере (λ = 1) главный ступенчатый вид нужен только для нахождения базисов M3 и M4. Базисы M1 и M2 нам оказались не нужны, зато нужны размерности этих подпространств, а они видны из любого ступенчатого вида (не главного). 2. Матрицы B − E и (B − E)2 сами оказались ступенчатыми, их вообще уже никуда не надо приводить (выше это сделано лишь для общности).
Учебное издание
Построение жорданова базиса
Составитель: АНДРЕЕВ Кирилл Кириллович
Методические указания рассмотрены и одобрены на заседании кафедры АМЛ 6 февраля 2009 года, протокол № 1-09.
Зав. кафедрой, профессор В. Л. Попов.
Редактор Технический редактор
Подписано в печать Формат 60´84/16. Бумага Усл. печ. л. Уч.-изд. л. Изд. № . Тираж 200 экз. Заказ . Московский государственный институт электроники и математики. 109028, Москва, Б. Трехсвятительский пер., 3/12. Отдел оперативной полиграфии Московского государственного института электроники и математики. 113054, Москва, М.Пионерская ул., 12. |



 , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
.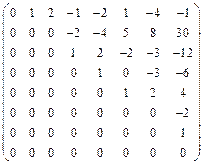 , B =
, B =  .
. , B =
, B =  .
.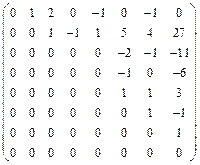 , B =
, B = 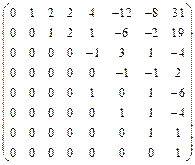 .
. , B =
, B = 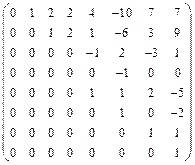 .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. , B =
, B =  .
. .
. , A3 =
, A3 =  , A4 = 0.
, A4 = 0.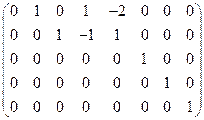 ;
; ;
; .
. ,
,  ,
, 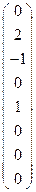 ñ; M2 = á
ñ; M2 = á  ,
,  ,
,  ,
,  ñ;
ñ; .
. , j2(e8) = A2e8 =
, j2(e8) = A2e8 =  , j3(e8) = A3e8 =
, j3(e8) = A3e8 =  .
.
 ®
® .
. , j2(e3) = A2e3 =
, j2(e3) = A2e3 =  ®
®  .
. .
. .
. .
. .
. ;
; ®
®  .
.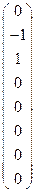 ; базис M2: e1, e2, e3, e4. Соединяем их в одну матрицу и приводим её к ступенчатому виду:
; базис M2: e1, e2, e3, e4. Соединяем их в одну матрицу и приводим её к ступенчатому виду: ®
®  .
.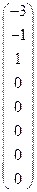 .
.
 ®
®  .
. . Вычисляем теперь
. Вычисляем теперь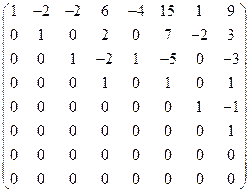 ®
®  ;
; ®
®  ;
; ®
®  .
. ,
,  ;
; = v.
= v. , (y − e)2(v) = (B − E)2v =
, (y − e)2(v) = (B − E)2v =  , (y − e)3(v) = (B − E)3v =
, (y − e)3(v) = (B − E)3v = 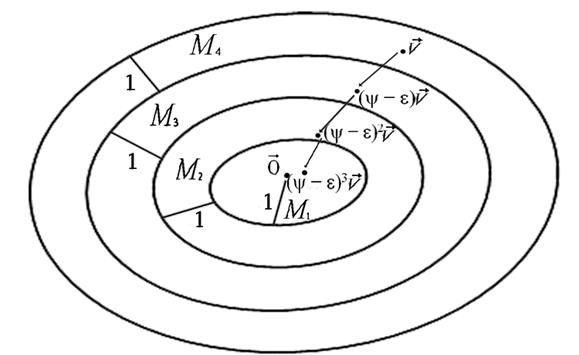
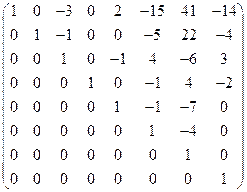 .
. ;
;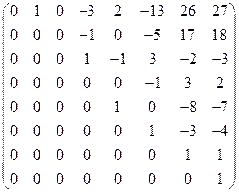 .
.