ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Построение графиков в MathCad

Постановка задачи:

1. Построить график функции f(x) согласно варианту из таблицы №1. Найти и записать приближенные корни уравнения f(x)=0 с помощью трассировки.

2. Построить два совмещенных графика f1(x) и f2(x), где f1(x)-f2(x)=f(x) на одной координатной плоскости. Найти и записать приближенные корни уравнения f(x)=0 с помощью трассировки.

3. Скопировать график функции f(x), на нем изменить стиль осей с ограничения на пересечение.

4. Найти точные корни уравнения f(x)=0, используя функцию root.

Типовой пример:

Задание 1. Построить график функции . Найти и записать приближенные корни уравнения f(x)=0 с помощью трассировки.

1. Выбираем на Панели инструментов графики (Graph) кнопку Координаты X-Y (X-Y-Plot) – появится пустой шаблон графика.

2. Вводим в метку оси y – функцию , а в метку оси x – неизвестную переменную x, нажимаем Enter – появится график функции.

3. Там, где функция пересекается с осью ox, там находятся корни уравнения. Отформатируем график для нахождения приближенных значений корней. Для этого:

3.1. щелкаем по графику левой кнопкой мыши, изменяем минимальные и максимальные пределы изменения по x (-5;5), по y (-3;3) и нажимаем Enter;

3.2. два раза щелкаем мышью по графику – появится диалоговое окно Formatting Currently Selected X-Y Axes. Окно содержит 4 корешка: Оси X-Y (X-Y Axes), Следы (Traces), Ярлыки (Labels), По умолчанию (Defaults).

3.3. в корешке Оси X-Y (X-Y Axes) расположены пункты для выбора форматирования осей графика:

Мерн. линейка (Log Scale) – нумерует оси в логарифмической последовательности;

Линии сетки (Grid Lines) – выводит вспомогательные линии сетки;

Пронумеровать (Numbered) – выводит нумерацию осей;

Автомасштаб (Autoscale) – устанавливает автоматический масштаб;

Показать маркеры (Show Markers) – устанавливает режим показа меток;

Авторешетка (Auto Grid) – устанавливает число вспомогательных линий сетки =2.

Число клеток решетки (Number Of Grid) – установка числа вспомогательных линий сетки.

Стиль осей (Axes Style) – позволяет выбрать стиль изображения осей графика:

Блочный (Boxed) – выводит график в рамке без осей;

Скрещив. (Crossed) – выводит график с осями;

Нет (None) – выводит график без осей и рамки.

Равные веса (Equal Scale) – устанавливает одинаковый масштаб по оси x и y.

Для нашего графика ставим галочки по каждой оси: Линии сетки (Grid Lines), Пронумеровать (Numbered), устанавливаем Число клеток решетки (Number of Grids) по оси x – 10, по оси y – 6, выбираем стиль осей - Блочный (Boxed).

3.4. в корешке Traces (Следы) находятся пункты для форматирования линий графика.

Подпись (Legend Label) – условный номер линии графика;

Символ (Symbol), Линия (Line), Цвет (Color), Тип (Type), Ширина (Weight) – устанавливают характеристики линии на графике.

Скрыть аргументы (Hide Arguments) – убирает с экрана подписи осей x и y;

Скрыть легенду (Hide Legend) – убирает с экрана подпись линии графика.

Для нашего графика меняем Цвет (Color) на голубой (blue) и ширину (Weight) делаем =2.

4. С помощью трассировки находим приближенные корни уравнения. Для этого щелкаем правой кнопкой по графику, выбираем команду Трассировка (Trace). С появлением окна X-Y-Trace щелкаем по кривой левой кнопкой мыши в точке пересечения кривой графика и оси x – в окне появляются значения x,y, где x – приближенный корень уравнения.

5. Оформить задание 1 как показано на рис. 1.

Рис. 1. График функции f(x)

Задание 2. Построить два совмещенных графика f1(x) и f2(x), где f1(x)-f2(x)=f(x) на одной координатной плоскости. Найти и записать приближенные корни уравнения f(x)=0 с помощью трассировки.

1. Разобьем функцию на две, перенеся в правую часть, получим . Построим на одном графике две функции y= и y= . Для этого выбираем кнопку X-Y-Plot – появится пустой шаблон графика.

2. Вводим в метку оси y - , затем ,, затем , а в метку оси x – неизвестную переменную x, нажимаем Enter – появится совмещенный график двух функций.

3. Там, где функции и пересекаются, там находятся корни уравнения. Отформатируем график аналогично, как в прошлом задании. С помощью трассировки найдем приближенные корни уравнения.

4. Оформить задание 2 как показано на рис. 2.

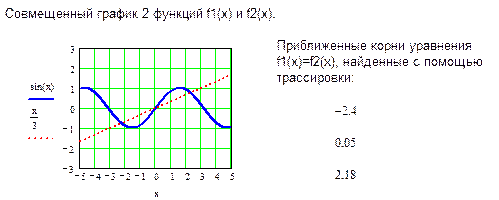
Рис. 2. Совмещенный график функций

Задание 3. Скопировать график функции f(x), на нем изменить стиль осей с ограничения на пересечение.

1. Выделяем график функции , обведя вокруг него рамку. В меню Правка (Edit) выбираем команду Копировать (Copy). Устанавливаем курсор там, где будет располагаться копируемый график. Выбираем в меню Правка (Edit) команду Вставить (Paste).

2. Два раза щелкаем мышью по графику – появится диалоговое окно Formatting Currently Selected X-Y Axes. В корешке Оси X-Y (X-Y Axes) галочку сменим с Блочный (Boxed) на Скрещив. (Crossed)

3. Оформить задание 3 как показано на рис. 3.

Рис. 3. График функции с осями

Задание 4. Найти точные корни уравнения f(x)=0, используя функцию root.

Варианты заданий:

Таблица 1

№	Вид функции f(x)	№	Вид функции f(x)
1.	sin(x) + 4x – 1	19.	x^1/2– 2sin(x)
2.	x³ + 5x – 3	20.	1/(2x) – cos(x)
3.	e^x + x² – 3	21.	3sin(x) – x² + 1
4.	e^x + 2x – 2	22.	cos(x) – 2x²
5.	x³ + 5x² – 1 – x	23.	x^1/3 – cos(3x)
6.	x² - 20sin(x)	24.	tg(x) – 2x
7.	ctg(x) – x/10	25.	lg(x) – 2cos(x)
8.	x³ – 3x² – 9x + 2	26.	2ln(x) – x³ + 6
9.	x³ – 6x – 8	27.	3ln(x) – x/4 – 1
10.	tg(0,5x ) – x²	28.	2ln(x) – 1/x
11.	5^x – 1 – 2cos(x)	29.	e^x + x² – 2
12.	ctg(x) – x/2	30.	x³ + 4x² – 8
13.	e^-x – (x – 1)²	31.	ln(x) + 7/(2x + 6)
14.	x×ln(x) – 1	32.	e^-x - x²
15.	2^x – 2x² + 1	33.	ln(x) – x^-2
16.	x - 0,5sin(x) – 2	34.	x - sin(x) – 0,25
17.	2cos(x) – (x²)/2	35.	x - 3cos²(x)
18.	x² – (x )^–2 + 10x

Контрольные вопросы:

Уметь:

Изменять максимальные и минимальные пределы по оси x и по оси y.
Изменять размер сетки по оси x и по оси y.
Строить вспомогательные линии по оси x и по оси y.
Изменять цвет и толщину кривой графика.
Найти корни а) приближенные с помощью трассировки и б) точные.