 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| АЛГОРИТМ ВЫЧИСЛЕНИЯ ПОКАЗАТЕЛЕЙ И ЭКОНОМИЧЕСКИЙ АНАЛИЗ ПОЛУЧЕННЫХ ДАННЫХ
1. По имеющимся в таблице 1 значениям показателей: A, a, g, m, a, φ, K0, L0, используя табличный редактор Excel, рассчитать: · по формуле (18) – зависимость X(t); · по формуле (9) – зависимость I(t); · по формуле (7) – зависимость  · по формуле (10) – зависимость C(t); · по формуле (6) – зависимость L(t), кроме значения L(0)=L0; · по формуле:  - зависимость K(t), кроме значения K(0)=K0. - зависимость K(t), кроме значения K(0)=K0. Значения t задаём в пределах от 0 до 50 лет с интервалом  году. Полученные результаты записаны в таблице 2. году. Полученные результаты записаны в таблице 2. Таблица 2 | t | X(t) | I(t) |  | C(t) | L(t) | K(t) | | | | | | | | | 324,450 | 116,802 | 93,052 | 77,868 | 95,000 | 950,000 | | 350,322 | 126,116 | 100,040 | 84,077 | 100,874 | 1043,052 | | 377,906 | 136,046 | 107,469 | 90,697 | 107,112 | 1143,091 | | 407,309 | 146,631 | 115,367 | 97,754 | 113,736 | 1250,560 | | 438,647 | 157,913 | 123,765 | 105,275 | 120,769 | 1365,928 | | 472,039 | 169,934 | 132,692 | 113,289 | 128,237 | 1489,692 | | 507,616 | 182,742 | 142,182 | 121,828 | 136,166 | 1622,384 | | 545,515 | 196,385 | 152,271 | 130,924 | 144,586 | 1764,566 | | 585,880 | 210,917 | 162,996 | 140,611 | 153,527 | 1916,837 | | 628,868 | 226,392 | 174,397 | 150,928 | 163,021 | 2079,833 | | 674,641 | 242,871 | 186,515 | 161,914 | 173,101 | 2254,230 | | 723,376 | 260,415 | 199,397 | 173,610 | 183,805 | 2440,745 | | 775,256 | 279,092 | 213,089 | 186,061 | 195,171 | 2640,142 | | 830,479 | 298,973 | 227,642 | 199,315 | 207,240 | 2853,230 | | 889,255 | 320,132 | 243,110 | 213,421 | 220,055 | 3080,872 | | 951,804 | 342,649 | 259,550 | 228,433 | 233,662 | 3323,982 | | 1018,363 | 366,611 | 277,022 | 244,407 | 248,111 | 3583,532 | | 1089,182 | 392,106 | 295,592 | 261,404 | 263,454 | 3860,554 | | 1164,528 | 419,230 | 315,326 | 279,487 | 279,745 | 4156,146 | | 1244,683 | 448,086 | 336,299 | 298,724 | 297,043 | 4471,472 | | 1329,946 | 478,781 | 358,586 | 319,187 | 315,411 | 4807,771 | | 1420,638 | 511,430 | 382,271 | 340,953 | 334,915 | 5166,358 | | | | | | | | | 1517,095 | 546,154 | 407,438 | 364,103 | 355,625 | 5548,628 | | 1619,677 | 583,084 | 434,182 | 388,723 | 377,616 | 5956,067 | | 1728,767 | 622,356 | 462,600 | 414,904 | 400,966 | 6390,249 | | 1844,769 | 664,117 | 492,796 | 442,745 | 425,760 | 6852,849 | | 1968,114 | 708,521 | 524,880 | 472,347 | 452,088 | 7345,645 | | 2099,259 | 755,733 | 558,970 | 503,822 | 480,044 | 7870,524 | | 2238,689 | 805,928 | 595,191 | 537,285 | 509,728 | 8429,494 | | 2386,920 | 859,291 | 633,674 | 572,861 | 541,248 | 9024,685 | | 2544,499 | 916,020 | 674,561 | 610,680 | 574,717 | 9658,359 | | 2712,008 | 976,323 | 718,000 | 650,882 | 610,255 | 10332,919 | | 2890,064 | 1040,423 | 764,150 | 693,615 | 647,991 | 11050,919 | | 3079,323 | 1108,556 | 813,180 | 739,037 | 688,061 | 11815,069 | | 3280,481 | 1180,973 | 865,267 | 787,315 | 730,608 | 12628,249 | | 3494,277 | 1257,940 | 920,602 | 838,626 | 775,786 | 13493,516 | | 3721,497 | 1339,739 | 979,386 | 893,159 | 823,758 | 14414,118 | | 3962,974 | 1426,670 | 1041,833 | 951,114 | 874,696 | 15393,503 | | 4219,593 | 1519,053 | 1108,170 | 1012,702 | 928,785 | 16435,336 | | 4492,295 | 1617,226 | 1178,639 | 1078,151 | 986,217 | 17543,506 | | 4782,079 | 1721,548 | 1253,495 | 1147,699 | 1047,202 | 18722,145 | | 5090,004 | 1832,401 | 1333,010 | 1221,601 | 1111,957 | 19975,640 | | 5417,196 | 1950,191 | 1417,474 | 1300,127 | 1180,717 | 21308,650 | | 5764,852 | 2075,347 | 1507,193 | 1383,564 | 1253,728 | 22726,125 | | 6134,239 | 2208,326 | 1602,493 | 1472,217 | 1331,254 | 24233,318 | | 6526,708 | 2349,615 | 1703,719 | 1566,410 | 1413,575 | 25835,811 | | 6943,688 | 2499,728 | 1811,239 | 1666,485 | 1500,985 | 27539,531 | | 7386,701 | 2659,212 | 1925,443 | 1772,808 | 1593,801 | 29350,770 | | 7857,361 | 2828,650 | 2046,745 | 1885,767 | 1692,356 | 31276,213 | | 8357,381 | 3008,657 | 2175,583 | 2005,772 | 1797,005 | 33322,958 | | 8888,583 | 3199,890 | 2312,426 | 2133,260 | 1908,126 | 35498,541 | Затем, применив "Мастер диаграмм" табличного редактора Excel, строим графики зависимостей: X(t), I(t),  C(t), L(t), K(t) (Приложение 1). C(t), L(t), K(t) (Приложение 1). 2. Далее используя формулу (23), определяем значение фондовооружённости труда для стационарной траектории  а по формуле: а по формуле:  (36) (36)
значение фондовооружённости  при одинаковой скорости роста функций h1(k) и h2(k). Получаем в результате следующие значения: при одинаковой скорости роста функций h1(k) и h2(k). Получаем в результате следующие значения:  а а  3. На основе ранее полученных данных, рассчитываем и строим функции изменения относительных показателей (Приложение 2):     (37) (37)
Полученные результаты записаны в таблице 3. Таблица 3 | t | k(t) | x(t) | c(t) | i(t) | | | | | | | 10,000 | 3,415 | 0,820 | 1,229 | | 10,340 | 3,473 | 0,833 | 1,250 | | 10,672 | 3,528 | 0,847 | 1,270 | | 10,995 | 3,581 | 0,859 | 1,289 | | 11,310 | 3,632 | 0,872 | 1,308 | | 11,617 | 3,681 | 0,883 | 1,325 | | 11,915 | 3,728 | 0,895 | 1,342 | | 12,204 | 3,773 | 0,906 | 1,358 | | 12,485 | 3,816 | 0,916 | 1,374 | | 12,758 | 3,858 | 0,926 | 1,389 | | 13,023 | 3,897 | 0,935 | 1,403 | | 13,279 | 3,936 | 0,945 | 1,417 | | 13,527 | 3,972 | 0,953 | 1,430 | | 13,768 | 4,007 | 0,962 | 1,443 | | 14,000 | 4,041 | 0,970 | 1,455 | | 14,226 | 4,073 | 0,978 | 1,466 | | 14,443 | 4,104 | 0,985 | 1,478 | | 14,654 | 4,134 | 0,992 | 1,488 | | 14,857 | 4,163 | 0,999 | 1,499 | | 15,053 | 4,190 | 1,006 | 1,508 | | 15,243 | 4,217 | 1,012 | 1,518 | | 15,426 | 4,242 | 1,018 | 1,527 | | 15,602 | 4,266 | 1,024 | 1,536 | | 15,773 | 4,289 | 1,029 | 1,544 | | 15,937 | 4,312 | 1,035 | 1,552 | | 16,096 | 4,333 | 1,040 | 1,560 | | 16,248 | 4,353 | 1,045 | 1,567 | | 16,395 | 4,373 | 1,050 | 1,574 | | 16,537 | 4,392 | 1,054 | 1,581 | | 16,674 | 4,410 | 1,058 | 1,588 | | 16,805 | 4,427 | 1,063 | 1,594 | | 16,932 | 4,444 | 1,067 | 1,600 | | 17,054 | 4,460 | 1,070 | 1,606 | | 17,172 | 4,475 | 1,074 | 1,611 | | 17,285 | 4,490 | 1,078 | 1,616 | | 17,393 | 4,504 | 1,081 | 1,622 | | 17,498 | 4,518 | 1,084 | 1,626 | | 17,599 | 4,531 | 1,087 | 1,631 | | 17,696 | 4,543 | 1,090 | 1,636 | | 17,789 | 4,555 | 1,093 | 1,640 | | 17,878 | 4,567 | 1,096 | 1,644 | | | | | | | 17,964 | 4,578 | 1,099 | 1,648 | | 18,047 | 4,588 | 1,101 | 1,652 | | 18,127 | 4,598 | 1,104 | 1,655 | | 18,203 | 4,608 | 1,106 | 1,659 | | 18,277 | 4,617 | 1,108 | 1,662 | | 18,348 | 4,626 | 1,110 | 1,665 | | 18,416 | 4,635 | 1,112 | 1,668 | | 18,481 | 4,643 | 1,114 | 1,671 | | 18,544 | 4,651 | 1,116 | 1,674 | | 18,604 | 4,658 | 1,118 | 1,677 | 4. Определяем величину L(0) по следующей формуле:  . . Получаем следующее значение L(0)= 95. Далее изменяем значение L(0) таким образом, чтобы получить выполнение условий:     Тогда для Тогда для  значение L(0)= 45,41, для значение L(0)= 45,41, для  значение L(0)> 239,29, для значение L(0)> 239,29, для  L(0) должно находится в следующем неравенстве 45,41<L(0)< 239,29 и для L(0) должно находится в следующем неравенстве 45,41<L(0)< 239,29 и для  значение L(0) определяется из следующего неравенства L(0)< 45,41. значение L(0) определяется из следующего неравенства L(0)< 45,41. 5. Рассчитаем коэффициенты фондовооружённости труда 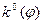 для стационарных траекторий при изменении нормы накопления для стационарных траекторий при изменении нормы накопления  в пределах от 0 до 1 с шагом равным 0,1, используя формулу (23). в пределах от 0 до 1 с шагом равным 0,1, используя формулу (23). Тогда получаем: Таблица 4  | k0(  ) ) | | | | 0,1 | 0,581 | | 0,2 | 2,325 | | 0,3 | 5,231 | | 0,4 | 9,299 | | 0,5 | 14,53 | | 0,6 | 20,923 | | 0,7 | 28,478 | | 0,8 | 37,196 | | 0,9 | 47,076 | | 58,118 | 6. Для каждого коэффициента фондовооруженности труда k0(f) и соответствующего ему коэффициента величины нормы накопления  рассчитываем значения функций: рассчитываем значения функций: А) X(t) по формуле (18); Б) I(t) по формуле (9); В) 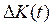 по формуле (7); по формуле (7); Г) C(t) по формуле (10); Д) K(t) по формуле:  ; кроме значения K(0) = K0. ; кроме значения K(0) = K0. Е) L(t) по формуле  для выбранного значения φ; для выбранного значения φ; Ж) k(t) = k0 по формуле  ; ; З) x(t) = x0 по формуле  ; ; И) c(t) = c0 по формуле  ; ; Й) i(t) = i0 по формуле  . . Значения t задать в пределах от 0 до 10 лет с интервалом  году. Вычисления приведены в таблице 5. году. Вычисления приведены в таблице 5. Таблица 5 | t | X(t) | I(t) | 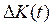 | C(t) | L(t) | K(t) | k(t) | x(t) | c(t) | i(t) | | 0,000 | 0,000 | -23,750 | 0,000 | 0,000 | 950,000 | | 0,000 | 0,000 | 0,000 | | 1312,188 | 78,731 | 55,575 | 708,581 | 1593,735 | 926,250 | 0,581 | 0,823 | 0,445 | 0,049 | | 695,459 | 83,455 | 58,910 | 333,821 | 422,340 | 981,825 | 2,325 | 1,647 | 0,790 | 0,198 | | 491,458 | 88,462 | 62,444 | 206,412 | 198,969 | 1040,735 | 5,231 | 2,470 | 1,037 | 0,445 | | 390,709 | 93,770 | 66,191 | 140,655 | 118,635 | 1103,179 | 9,299 | 3,293 | 1,186 | 0,790 | | 331,321 | 99,396 | 70,162 | 99,396 | 80,482 | 1169,369 | 14,530 | 4,117 | 1,235 | 1,235 | | 292,667 | 105,360 | 74,372 | 70,240 | 59,244 | 1239,531 | 20,923 | 4,940 | 1,186 | 1,778 | | 265,909 | 111,682 | 78,834 | 47,864 | 46,138 | 1313,903 | 28,478 | 5,763 | 1,037 | 2,421 | | 246,631 | 118,383 | 83,564 | 29,596 | 37,444 | 1392,738 | 37,196 | 6,587 | 0,790 | 3,162 | | 232,381 | 125,486 | 88,578 | 13,943 | 31,360 | 1476,302 | 47,076 | 7,410 | 0,445 | 4,001 | | 221,691 | 133,015 | 93,893 | 0,000 | 26,926 | 1564,880 | 58,118 | 8,233 | 0,000 | 4,940 | 7. На основании результатов вычислений, выполненных в предыдущем пункте, выписываем в отдельную таблицу значения среднедушевого потребления на стационарных траекториях (c0) и соответствующие этим значениям величины нормы накопления (φ). Полученные результаты представлены в таблице 6 Таблица 6 | φ | c(t) | | | | 0,1 | 0,445 | | 0,2 | 0,790 | | 0,3 | 1,037 | | 0,4 | 1,186 | | 0,5 | 1,235 | | 0,6 | 1,186 | | 0,7 | 1,037 | | 0,8 | 0,790 | | 0,9 | 0,445 | | | Затем, используя «Мастер диаграмм» табличного редактора Excel, строим график зависимостей  (Приложение 3). Сравнивая величину нормы накопления (φ), при которой достигается максимальное среднедушевое потребление (c0), с коэффициентом эластичности выпуска по основным производственным фондам (a). Значение нормы накопления (φ), при которой достигается максимальное среднедушевое потребление (c0)=0,5, т.е. оно совпадает с коэффициентом эластичности выпуска по основным производственным фондам (a)=0,5. (Приложение 3). Сравнивая величину нормы накопления (φ), при которой достигается максимальное среднедушевое потребление (c0), с коэффициентом эластичности выпуска по основным производственным фондам (a). Значение нормы накопления (φ), при которой достигается максимальное среднедушевое потребление (c0)=0,5, т.е. оно совпадает с коэффициентом эластичности выпуска по основным производственным фондам (a)=0,5. 8. Рассчитываем и строим, с применением табличного редактора Excel, функцию изменения среднедушевого потребления (c0) от нормы накопления (φ), используя формулу (24). Проверяя совпадение графиков зависимостей  , полученных при выполнении данного и предыдущего пункта между собой. , полученных при выполнении данного и предыдущего пункта между собой. Рассчитанная по формуле (24) норма накопления (φ), приведена в таблице7. Таблица 7 | φ | c(φ) | | | | | | 0,1 | 0,445 | | 0,2 | 0,790 | | 0,3 | 1,037 | | 0,4 | 1,186 | | 0,5 | 1,235 | | 0,6 | 1,186 | | 0,7 | 1,037 | | 0,8 | 0,790 | | 0,9 | 0,445 | | | Сравнивая полученные результаты из пунктов 7 и 8 видим, что значения среднедушевой нормы накопления совпадают, что говорит о правильности проведённых расчетов. График функции  приведён в приложение 4. приведён в приложение 4.
ЗАКЛЮЧЕНИЕ В данной работе была рассмотрена модель Солоу. При этом в исходной модели экономическая система рассматривается как единое целое, в которой производится один универсальный продукт. Были произведены расчеты абсолютных показателей, относительных показателей, абсолютных показателей с учетом запаздывания при вводе фондов. Было рассмотрено «золотое» правило накопления и построен график зависимости среднедушевого потребления от нормы накопления. На основании графика стало видно, что максимальное среднедушевое потребление достигается, когда норма накопления равна коэффициенту эластичности по основным производственным фондам. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. В.Ф.Пучков методическое пособие «Математические модели макроэкономики» - Гатчина :изд-во ЛОИЭФ, 2005. 2. Экономико-математические методы и прикладные модели: Уч. пособие / В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. – М.: ЮНИТИ.
ПРИЛОЖЕНИЕ 1 
ПРИЛОЖЕНИЕ 2 
ПРИЛОЖЕНИЕ 3 
ПРИЛОЖЕНИЕ 4
 ПРИЛОЖЕНИЕ 5 ПРИЛОЖЕНИЕ 5

ПРИЛОЖЕНИЕ 6 
ПРИЛОЖЕНИЕ 7  ПРИЛОЖЕНИЕ 8 ПРИЛОЖЕНИЕ 8
Функции изменения относительных показателей для случая k(0)>k 
|





 - зависимость K(t), кроме значения K(0)=K0.
- зависимость K(t), кроме значения K(0)=K0. году. Полученные результаты записаны в таблице 2.
году. Полученные результаты записаны в таблице 2.
 C(t), L(t), K(t) (Приложение 1).
C(t), L(t), K(t) (Приложение 1). а по формуле:
а по формуле: (36)
(36) при одинаковой скорости роста функций h1(k) и h2(k). Получаем в результате следующие значения:
при одинаковой скорости роста функций h1(k) и h2(k). Получаем в результате следующие значения:  а
а 



 (37)
(37) .
.


 Тогда для
Тогда для  значение L(0)= 45,41, для
значение L(0)= 45,41, для  значение L(0)> 239,29, для
значение L(0)> 239,29, для  L(0) должно находится в следующем неравенстве 45,41<L(0)< 239,29 и для
L(0) должно находится в следующем неравенстве 45,41<L(0)< 239,29 и для  значение L(0) определяется из следующего неравенства L(0)< 45,41.
значение L(0) определяется из следующего неравенства L(0)< 45,41.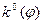 для стационарных траекторий при изменении нормы накопления
для стационарных траекторий при изменении нормы накопления  в пределах от 0 до 1 с шагом равным 0,1, используя формулу (23).
в пределах от 0 до 1 с шагом равным 0,1, используя формулу (23).
 рассчитываем значения функций:
рассчитываем значения функций: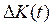 по формуле (7);
по формуле (7); для выбранного значения φ;
для выбранного значения φ; ;
; ;
; ;
; .
. году. Вычисления приведены в таблице 5.
году. Вычисления приведены в таблице 5. (Приложение 3). Сравнивая величину нормы накопления (φ), при которой достигается максимальное среднедушевое потребление (c0), с коэффициентом эластичности выпуска по основным производственным фондам (a). Значение нормы накопления (φ), при которой достигается максимальное среднедушевое потребление (c0)=0,5, т.е. оно совпадает с коэффициентом эластичности выпуска по основным производственным фондам (a)=0,5.
(Приложение 3). Сравнивая величину нормы накопления (φ), при которой достигается максимальное среднедушевое потребление (c0), с коэффициентом эластичности выпуска по основным производственным фондам (a). Значение нормы накопления (φ), при которой достигается максимальное среднедушевое потребление (c0)=0,5, т.е. оно совпадает с коэффициентом эластичности выпуска по основным производственным фондам (a)=0,5. , полученных при выполнении данного и предыдущего пункта между собой.
, полученных при выполнении данного и предыдущего пункта между собой.


 ПРИЛОЖЕНИЕ 5
ПРИЛОЖЕНИЕ 5

 ПРИЛОЖЕНИЕ 8
ПРИЛОЖЕНИЕ 8