 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пример составления полинома ЖегалкинаСовершенная дизъюнктивная нормальная форма Фиксируем алфавит булевых переменных Напомним, что Определение 1.Элементарной конъюнкцией ранга где Определение 2. Дизъюнктивной нормальной формой (ДНФ) относительно алфавита Отметим все важные свойства совершенных конъюнкций: а) произведение двух различных совершенных конъюнкций равно б) в совершенной дизъюнктивной нормальной форме относительно алфавита Действительно, при
c одержит для некоторого Теорема. Всякая функция алгебры логики
Дизъюнкция идет по всем наборам, в которых функция равна Вопрос. Чем является функция Ваш ответ : ДНФ (дизъюнктивная нормальная форма) Да, правильно. Так как во втором слагаемом нет переменной
Составление СДНФ Пример 1. Совершенные ДНФ для элементарных функций (табл. 2): для конъюнкции:
Пример 2. Написать СДНФ относительно алфавита
СДНФ для
Пример 3. Преобразовать в СДНФ формулу
Замечание. Если функция задана формулой, то можно для функции вычислить таблицу, а затем задача сведется к примеру 2. Однако создание таблицы может оказаться очень трудоемким. Так, например, если алфавит переменных состоит из
Вопрос. Сколько элементарных конъюнкций содержится в СДНФ для функции, заданной своими значениями Ваш ответ : Три Да, правильно. Потому что функция равна 1 только на трех наборах. Полином Жегалкина Элементарные конъюнкции вида Любая сумма по Теорема.Всякая функция алгебры логики представима полиномом Жегалкина единственным образом с точностью до перестановки слагаемых.
Вопрос. Чем является данная функция Ваш ответ : Произвольной функцией Да,правильно. Пример составления полинома Жегалкина
Пример 1. Пусть задана функция
Представим ее СДНФ Пример 2. Пусть задана функция формулой ДНФ функции Пример 3. Для элементарных функций табл. 2 полиномы Жегалкина имеют вид:
Вопрос. Чему равен полином Жегалкина для функции Ваш ответ :
Да, правильно. Начало формы Теорема двойственности Функция Из определения следует, что таблица для двойственной функции
Отношение двойственности симметрично, Пример 1. Двойственные функции к элементарным функциям табл. 2: Пример 2. Является ли функция Теорема двойственности. Пусть имеется формула (тождество) Доказательство. С помощью этой теоремы легко доказываются некоторые тождества. Например,
Замечание. Операция Вопрос. Является ли функция
Ваш ответ : Нет Правильно, так как таблица не симметрична. Определение СКНФ Элементарной дизъюнкцией ранга Любая конъюнкция элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ). Любая конъюнкция совершенных дизъюнкций называется совершенной конъюнктивной нормальной формой (СКНФ). Теорема. Всякая функция алгебры логики
Вопрос. Чем является функция Ваш ответ : КНФ Правильно, так как во второй скобке содержатся не все переменные. Примеры составления СКНФ
Пример 1. Совершенные КНФ для элементарных функций табл. 1 относительно алфавита переменных
Пример 2. Написать СКНФ для функции голосования.
СКНФ для
Пример 3. Преобразовать в СКНФ формулу
Вопрос. Как выглядит СКНФ для функции, заданной таблично?
Ваш ответ :
Правильно. |



 .
.
 относительно алфавита
относительно алфавита  назовем форму
назовем форму  ,
, . При
. При  конъюнкция называется совершенной.
конъюнкция называется совершенной. ;
; либо все совершенные конъюнкции равны нулю, либо равна
либо все совершенные конъюнкции равны нулю, либо равна  одна единственная конъюнкция.
одна единственная конъюнкция. произведение
произведение (1)
(1)
 множители
множители  и
и  , отсюда
, отсюда  , и поэтому произведение (1) равно
, и поэтому произведение (1) равно  уравнение
уравнение  влечет
влечет  ,...,
,...,  – единственно возможное решение, т.к. если для некоторого
– единственно возможное решение, т.к. если для некоторого  , то
, то 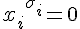 и нулю равна вся конъюнкция.
и нулю равна вся конъюнкция. представима совершенной дизъюнктивной нормальной формой относительно алфавита своих переменных
представима совершенной дизъюнктивной нормальной формой относительно алфавита своих переменных  ,..,
,..,  :
: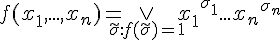 (2)
(2)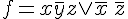 ?
? .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; :
:  ;
; :
: 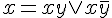 ;
; ;
; для функции голосования от трех переменных, заданной таблично (см. табл. 3).
для функции голосования от трех переменных, заданной таблично (см. табл. 3). содержит четыре совершенные конъ-юнкции (по числу единиц функции)
содержит четыре совершенные конъ-юнкции (по числу единиц функции)
 .
. относительно алфавита
относительно алфавита  есть ДНФ, но имеет несовершенные конъюнкции. С помощью преобразований вида
есть ДНФ, но имеет несовершенные конъюнкции. С помощью преобразований вида  доводим конъюнкции до совершенства:
доводим конъюнкции до совершенства: ,
, ,
, :
: .
. переменных, то таблица имеет
переменных, то таблица имеет  строк, что неприемлемо, так как потребуется много места на доске или бумаге.
строк, что неприемлемо, так как потребуется много места на доске или бумаге. ?
? ,
,  различных положительных конъюнкций называется полиномом Жегалкина. Константу
различных положительных конъюнкций называется полиномом Жегалкина. Константу  , то
, то  . (3)
. (3) , что приведет к формуле
, что приведет к формуле . (4)
. (4) , раскрывая скобки и приведя подобные члены по правилу
, раскрывая скобки и приведя подобные члены по правилу  , мы получим полином Жегалкина. Единственность представления функции полиномом следует из того, что полиномов Жегалкина под алфавитом
, мы получим полином Жегалкина. Единственность представления функции полиномом следует из того, что полиномов Жегалкина под алфавитом  переменных, то есть
переменных, то есть  . ▲
. ▲ ?
? таблицей.
таблицей. .
. .
. .
. .
. .
. ), поэтому
), поэтому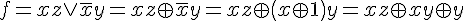 .
. ;
; ;
; ;
; ;
; ;
; ;
; ?
?
 называется двойственной к функции
называется двойственной к функции  .
. может быть получена из таблицы для функции
может быть получена из таблицы для функции  , то функция
, то функция  для любого набора
для любого набора  .
. ,
,  ,
, 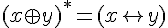 ,
, ,
,  ,
, 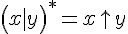 ,
, ,
,  ,
, 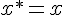 ,
,  ,
,  .
. самодвойственной?
самодвойственной?
 и
и  , и как только обнаружится, что на наборе
, и как только обнаружится, что на наборе  , значит, функция
, значит, функция  и
и  ,
, .
.



 . ▲
. ▲ и теоремы двойственности следует другая формула де Моргана, так как
и теоремы двойственности следует другая формула де Моргана, так как  влечет
влечет  ;
; (формула сокращения) следует
(формула сокращения) следует  , по теореме двойственности получаем другую формулу сокращения
, по теореме двойственности получаем другую формулу сокращения  ;
; получаем
получаем  и отсюда
и отсюда  .
. меняет приоритетность операндов, поэтому во избежание ошибок в начальной формуле надо отменить приоритетность, то есть должны быть расставлены все скобки, выделяющие бинарные операции.
меняет приоритетность операндов, поэтому во избежание ошибок в начальной формуле надо отменить приоритетность, то есть должны быть расставлены все скобки, выделяющие бинарные операции. назовем форму
назовем форму ,
, . При
. При  представима совершенной конъюнктивной нормальной формой
представима совершенной конъюнктивной нормальной формой .
. запишем СДНФ для функции
запишем СДНФ для функции  ,
,
 , что и требовалось доказать. ▲
, что и требовалось доказать. ▲ ?
? ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;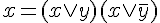 ;
; ;
;
 .
. .
.
 .
.