 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Проектирование БИХ-фильтра в графической среде FDATool
Цифровой фильтр Курсовой проект Пояснительная записка
Руководитель: Рогозин А.Н. Автор проекта: студент группы ПС-541 Новиков И.В.
Работа защищена с оценкой _________________ “___”___________2012г.
Челябинск, 2012г.
Техническое задание
Ч1 – фильтр Чебышева первого рода; БП – билинейное Z-преобразование;
В курсовом проекте будет произведен синтез БИХ фильтра нижних частот, с заданными параметрами. Расчет фильтра и построение основных характеристик будет проводиться при помощи стандартных средств MatLab, проверка полученных данных – при помощи специализированных функций MatLab (FDA Tool).
Содержание
Техническое задание……………………………………….2 Введение…………………………………………………….4 Проектирование БИХ-фильтра………………………….…7 MatLab программа…………….………………………….…24 Заключение………………………………………..…………27 Список литературы……………………….…………………28
Требования к фильтрам могут формулироваться как во временной, так и в частотной областях, что определяется назначением фильтра и областью его описания. Во временной областитребования могут задаваться к импульсной В частотной области требования могут предъявляться: · только к АЧХ или к характеристике ослабления (затухания) без каких-либо ограничений на ФЧХ; · только к ФЧХ, когда важно сохранение фазовых, а потому и временных соотношений между гармоническими составляющими принимаемого сигнала; это – фазовые корректоры; · одновременно и к АЧХ, и к ФЧХ; например, возможен синтез КИХ-фильтров с заданной АЧХ и линейной ФЧХ. Рассмотрим задание требований к частотно-избирательным ЦФ. На рис. 1 представлена идеальная АЧХ ФНЧ и, вследствие физической невозможности ее реализации, аппроксимация при заранее определяемых допусках, зависящих от ряда практических ограничений. Эти ограничения связаны, прежде всего, с назначением синтезируемого фильтра. Все ограничения и допуски составляют требования, предъявляемые к фильтру. Требования к фильтрам включают в себя: 1. Задание частоты дискретизации 2. задание требований к АЧХ При этом необходимо помнить, что: · · требования не задаются в переходных полосах избирательных фильтров; · требования формулируются в виде допустимых отклонений от нормированной АЧХ · размерность 3. Выбор метода аппроксимации АЧХ Диаграмма идеальной АЧХ ФНЧ и диаграмма допусков к отклонениям АЧХ в полосах пропускания и задерживания представлены на рис. 1. При постановке задачи синтеза идеальную АЧХ будем обозначать Фильтр нижних частот (ФНЧ) имеет три частотных полосы (рис. 1): полосу пропускания (ПП), полосу задерживания (ПЗ), или ослабления, и переходную полосу.
Важным является то обстоятельство, что в соответствии с методом синтез КИХ-фильтров отклонение АЧХ от 1 (соответст Полоса задерживания (ослабления) (ПЗ) лежит в пределах от граничной частоты Переходная полоса располагается между полосами пропускания и задерживания; ее ширина
Проектирование БИХ-фильтра 1. Задание на синтез ЦФ следующее:
Ч1 – фильтр Чебышева первого рода; БП – билинейное Z-преобразование;
2. Определив минимально необходимый порядок фильтра функцией cheb1ord, с помощью функции cheby1 получим коэффициенты
Перейдём от цифровых частот к аналоговым по формуле:
В нашем случае:
С помощью MatLab рассчитаем аналоговый фильтр прототип. а)Определим минимально необходимый порядок фильтра: Для этого используем функцию MatLab: [n, Wo] = cheb1ord(Wp, Ws, Rp, Rs, ‘s’), в этой функции: n – минимально необходимый для заданных требований порядок фильтра; Wo – частота среза фильтра; Wp - граница полосы пропускания рад/с; Ws - граница полосы задерживания рад/с; Rp – допустимый уровень пульсаций в полосе пропускания, дб ; Rs – допустимый уровень пульсаций в полосе задеживания, дб. Параметр ‘s’ является признаком аналогового расчета. В нашем случае:
б) Рассчитаем коэффициенты передачи аналогового фильтра: Для этого используем функцию MatLab: [b, a] = cheby1(n, Wo, type, ‘s’), в этой функции: type – тип фильтра; Wo – частота среза фильтра; n – порядок фильтра;
Тогда предаточная функция АФ-прототипа:
Построим частотные характеристики :
Для того чтобы убедиться в удовлетворении начальным требованиям, построим ЛАЧХ:
3. Рассчитаем полюсы АФ-прототипа :
4. По вычисленным с помощью функции tf2zp векторам нулей и полюсов определим векторы коэффициентов числителя b и знаменателя a передаточной функции ЦФ:
Запишем саму передаточную функцию ЦФ :
Тот же результат получается при использовании стандартной функции bilinear. Синтаксис функции: [bz, az] = bilinear(b,a,Fs,Fp); Здесь b и a – коэффициенты полиномов числителя и знаменателя функции передачи АФ-прототипа. Параметр Fs задает частоту дискретизации в герцах. Последний входной параметр Fp является необязательным. Если при вызове использован параметр Fp, то он задает частоту (в герцах), на которой комплексные коэффициенты передачи аналоговой и дискретной системе будут совпадать.
Fs = 30000 Гц. Параметр Fp при вызове функции я не использовал.
Построим диаграмму нулей и полюсов :
Преобразуем передаточную функцию:
Разностное уравнение имеет вид:
Обозначим коэффициенты знаменателя передаточной функции как:
Обозначим коэффициенты знаменателя передаточной функции как:
Решение разностного уравнения для управляющего сигнала типа единичный скачок представим в виде диаграммы :
Построим импульсную и переходную характеристики фильтра: Для построения импульсной характеристики фильтра используем функцию MatLab h = impz(b, a, n); где: h – отсчёты импульсной характеристики; b – вектор коэффициентов числителя передаточной функции цифрового фильтра; a - вектор коэффициентов знаменателя передаточной функции цифрового фильтра; n – число отсчётов импульсной характеристики. Для построения переходной характеристики фильтра подадим на фильтр ряд единичных скачков: g = filter(b, a, ones(1, n)); где: g – отсчёты переходной характеристики; b – вектор коэффициентов числителя передаточной функции цифрового фильтра; a - вектор коэффициентов знаменателя передаточной функции цифрового фильтра; n – число отсчётов переходной характеристики характеристики
Построим сигналы на выходе фильтра, подавая на вход сигналы (синусоиды y=10∙Sin(2πf∙t) ) с различными частотами, лежащими в полосе задержки и в полосе пропускания.
Из графиков видно, что сигнал с частотой, лежащей в полосе пропускания не изменяется, после прохождения через фильтра.
Сигнал, с частотой, лежащей в полосе задерживания практически полностью подавляется.
Графики можно сверить с частотными характеристиками и убедиться в их правильности. Так как все полюсы лежат внутри единичной окружности, то фильтр является устойчивым. Для составления канонической структурной схемы фильтра (рис. 28) запишем уравнения:
Запишем коэффициенты числителя и знаменателя передаточной функции:
Каноническая структура схемы имеет вид :
Составим структурную схему фильтра в последовательной форме, для этого представим передаточную функцию
параметры каскадного представления задаются в виде матрицы, содержащей вещественные коэффициенты:
Матрицу
Структурная схема имеет вид:
В MatLab для расчета частотных характеристик ЦФ используется функция
Логарифмическая АЧХ ЦФ имеет вид :
Масштабированная ЛАЧХ:
Построим логарифмические характеристики в функции абсолютной псевдочастоты
С последующей заменой комплексной переменной Удобство псевдочастоты заключается в том, что, как следует из (8), на частоте где выполняется условие Для перехода от дискретной передаточной функции разомкнутой и [H_CF W_CF] = freqz(bz,az); lam = 2*f_d*tan(W_CF*f_d/(4*f_d)); lam_p = 2*f_d*tan(w_p/(2*f_d)); lam_s = 2*f_d*tan(w_s/(2*f_d)); plot(lam,LACH_CF);
Проектирование БИХ-фильтра в графической среде FDATool Для проверки истинности результатов проведем синтез КИХ-фильтра в графической среде FDATool.
АЧХ фильтра, сходится с рассчитанной ранее
ФЧХ фильтра, так же сходится
Импульсная, переходная характеристики и диаграмму полюсов и нулей так же соответствуют полученным ранее в расчете. Импульсная характеристика
Диаграмма нулей и полюсов
Фильтры рассчитанные в среде FDAtool и с помощью системы MatLab идентичны.
close all; clear all; clc; f_d = 30000; w_d = 2*pi*f_d; %Частота дискретизации F_p = 1000; w_p = 2*pi*F_p; %Частота среза R_p = 0.7; R_s = 55; %Заданные допуски на ЛАЧХ F_s = 7000; w_s = 2*pi*F_s; %Граничная частота [N, W_0] = cheb1ord(w_p,w_s,R_p,R_s,'s'); %Расчитываем минемально необходимый порядок и частоту среза фильтра [b, a] = cheby1(N,R_p,W_0,'s'); %Рассчитаем коэфф. передаточной функции АФ W = 0:5:w_d/2; H = freqs(b,a,W); %Вычисление отсчетов комплексной АЧХ ACH = abs(H); %Вычисление АЧХ LACH = 20*log10(ACH); %Вычисление логарифмической АЧХ FCH = unwrap(angle(H))*180/pi; %Вычисление ФЧХ %Построение частотных характеристик figure('name','Частотные характеристики'); subplot(2,1,1); plot(W/(2*pi),ACH); hold on; plot([0 W_0/(2*pi) 1.00001*W_0/(2*pi) w_d/(4*pi)], [1 1 0 0], '-.r'); grid on; legend('ACH AF','ACH IdealF'); title('ACH'); xlabel('f, Hz'); ylabel('Amplitude'); subplot(2,1,2); plot(W/(2*pi),FCH); grid on; title('FCH'); xlabel('f, Hz'); ylabel('Fase(gradus)'); %Построение ЛАЧХ figure('name','Логарифмическая АЧХ'); plot(W/(2*pi),LACH); grid on; title('LACH'); xlabel('f, Hz'); ylabel('Amplitude(dB)'); %Построение диаграммы полюсов figure('name', 'Диаграмма полюсов АФ'); [z, p, k] = zplane(b,a); grid on; xlabel('Real'); ylabel('Imag'); %БП [z, p, k] = tf2zp(b, a); z_CF = (2*f_d+z)./(2*f_d-z); p_CF = (2*f_d+p)./(2*f_d-p); k_CF = k * prod(2*f_d - z)/prod(2*f_d - p); Num = length(z) - length(p); switch (Num > 0) case 0 z_CF = [z_CF; ones(abs(Num),1)*(-1)]; case 1 p_CF = [p_CF; ones(abs(Num),1)*(-1)]; end [bz, az]=zp2tf(z_CF, p_CF, k_CF);
[bz1, az1] = bilinear(b,a,f_d); [zz, pz, kz] = bilinear(z, p, k, f_d);
%Построение диаграммы нулей и полюсов ЦФ figure('name', 'Диаграмма нулей и полюсов ЦФ'); zplane(bz, az); grid on; xlabel('Real'); ylabel('Imag'); %Решение разностного уравнения методом итерационной процедуры x=ones(1, 100); h1 = impz(bz,az,100); x1=zeros(1,length(h1)-20); x1 = [x,x1]; for n = 1:length(h1) y(n) = 0; for m=1:n y1= x1(m)*h1(n-m+1); y(n)=y(n)+y1; end; end; figure('name', 'Кривая переходного процесса'); stem(0:length(x)-1, y(1:length(x))); grid on; %Построение переходной и импульсной характеристики figure('name', 'Переходная и импульсная х-ки'); pereh = filter(bz, az, ones(1, length(h1))); subplot(2,1,1); stem((0:length(h1)-1), h1); grid on; title('Impulsnaja'); xlabel('n'); ylabel('Amplitude'); xlim([0 length(h1)]); subplot(2,1,2); stem((0:length(pereh)-1), pereh); grid on; title('Perehodnaja'); xlabel('n'); ylabel('Amplitude'); xlim([0 length(h1)]); %Построение реакции фильтра на различные входные сигналы figure('name', 'Реакция фильтра на различные входные сигналы'); f1 = 400; f2 = 2500; t_sign = 0:1/f_d:0.01; signal_1 = 10*sin(2*pi*f1*t_sign); signal_2 = 10*sin(2*pi*f2*t_sign); vyx1 = filtfilt(bz, az, signal_1); vyx2 = filtfilt(bz, az, signal_2); subplot(2,2,1); plot(t_sign, signal_1, 'r-'); grid on; title('800 Hz'); subplot(2,2,2); plot(t_sign, vyx1, 'k-'); grid on; subplot(2,2,3); plot(t_sign, signal_2, 'r-'); grid on; title('2000 Hz'); subplot(2,2,4); plot(t_sign, vyx2, 'k-'); grid on; %Построение частотных характеристик ЦФ figure('name', 'Частотные характеристики фильтра'); [H_CF W_CF] = freqz(bz,az); ACH_CF = abs(H_CF); LACH_CF = 20*log10(ACH_CF); FCH_CF = angle(H_CF); FCH_CF = unwrap(FCH_CF); %Устранение скачков subplot(2,1,1); plot(W_CF*f_d/(2*pi),ACH_CF,'k'); grid on; hold on; plot(W/(2*pi),ACH,'-.g') title('ACH'); xlabel('f, Hz'); ylabel('Amplitude'); legend('ACH CF','ACH AF'); subplot(2,1,2); plot(W_CF*f_d/(2*pi),FCH_CF*180/pi,'k'); grid on; hold on; plot(W/(2*pi),FCH,'-.g') title('FCH'); xlabel('f, Hz'); ylabel('Fase(gradus)'); legend('FCH CF','FCH AF'); figure('name', 'Логарифмическая АЧХ'); plot(W_CF*f_d/(2*pi),LACH_CF); hold on; %построение границы полос пропускания и задержки plot([F_s, F_s], [-250, -R_s], 'r--'); plot([F_s, max(W_CF*f_d/(2*pi))], [-R_s, -R_s], 'r--'); plot([F_p, F_p], [50, -R_p], 'r--'); plot([0, F_p], [-R_p, -R_p], 'r--'); hold off; grid on; xlabel('f, Hz'); ylabel('Amplitude(dB)'); %Построение ЛАЧХ ЦФ в функции абсолютной псевдочастоты lam = 2*f_d*tan(W_CF*f_d/(4*f_d)); lam_p = 2*f_d*tan(w_p/(2*f_d)); lam_s = 2*f_d*tan(w_s/(2*f_d)); figure('name', 'Логарифмическая АЧХ в функции абсолютной псевдочастоты'); plot(lam,LACH_CF); hold on; %построение границы полос пропускания и задержки plot([lam_s, lam_s], [-215, -R_s], 'r--'); plot([lam_s, max(lam)], [-R_s, -R_s], 'r--'); plot([lam_p, lam_p], [50, -R_p], 'r--'); plot([0, lam_p], [-R_p, -R_p], 'r--'); hold off; axis([0 lam(length(lam)) LACH_CF(length(LACH_CF)) 50]); grid on; xlabel('lam'); ylabel('Amplitude(dB)');
[sos,g] = tf2sos(bz,az)
Заключение Синтез БИХ-фильтра нижних частот с требуемыми параметрами был проведен успешно. Разработка проводилась без использования стандартных функций для синтеза ЦФ и с их использованием. Результаты получились идентичными. Проверка полученных результатов в графической среде FDATool показала, что расчет фильтра был произведен верно.
Литература 1. Синтез цифровых фильтров: руководство к курсовой работе /Сост. Г.В. Малинин, Н.М. Лазарева; Чуваш. ун-т. Чебоксары, 2006. 68 с. 2. Цифровая обработка сигналов/А. Б. Сергиенко – СПб.: Питер, 2002. – 608 с. 3. Сигналы и их обработка в электронных устройствах: Учебное пособие/Белов Г. А.; Чебоксары: Изд-во Чуваш. ун-та, 1996. 376 с.
|



 , дБ
, дБ , дБ
, дБ , кГц
, кГц , кГц
, кГц
 Введение
Введение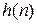 или переходной
или переходной 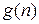 характеристике при широких допусках к частотным свойствам фильтра.
характеристике при широких допусках к частотным свойствам фильтра. [Гц] и типа избирательности (НЧ, ВЧ и т. д.).
[Гц] и типа избирательности (НЧ, ВЧ и т. д.). или к характеристике затухания
или к характеристике затухания  , представляющей собой логарифмическую АЧХ.
, представляющей собой логарифмическую АЧХ. задание требований начинается с установки всех граничных частот фильтра только в основной полосе частот
задание требований начинается с установки всех граничных частот фильтра только в основной полосе частот  ;
;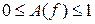 и отображаются на диаграмме допусков;
и отображаются на диаграмме допусков; .
. .
. Полоса пропускания (ПП) ограничивается частотой среза
Полоса пропускания (ПП) ограничивается частотой среза  ; ширина полосы пропускания
; ширина полосы пропускания  ;
;  – максимально допустимое отклонение от 1;
– максимально допустимое отклонение от 1;  – допустимый уровень пульсаций в полосе пропускания.
– допустимый уровень пульсаций в полосе пропускания. венно,
венно,  , а для БИХ-фильтров отклонение задается только в одну сторону так, чтобы АЧХ не превышало единицы. Это означает, что для БИХ-фильтра, синтезируемого с теми же допусками, что и КИХ-фильтр, необходимо задавать в полосе пропускания допустимое отклонение АЧХ
, а для БИХ-фильтров отклонение задается только в одну сторону так, чтобы АЧХ не превышало единицы. Это означает, что для БИХ-фильтра, синтезируемого с теми же допусками, что и КИХ-фильтр, необходимо задавать в полосе пропускания допустимое отклонение АЧХ  (причина, по которой в полосе пропускания требования к БИХ-фильтрам задаются не превышающими единицы, состоит в их синтезе по аналоговым фильтрам-прототипам).
(причина, по которой в полосе пропускания требования к БИХ-фильтрам задаются не превышающими единицы, состоит в их синтезе по аналоговым фильтрам-прототипам). до половины частоты дискретизации
до половины частоты дискретизации  ; ее ширина
; ее ширина  ;
;  – максимально допустимое отклонение АЧХ от 0;
– максимально допустимое отклонение АЧХ от 0;  – минимально необходимое затухание в полосе задерживания.
– минимально необходимое затухание в полосе задерживания. ; поскольку в этой полосе требования не задаются, удовлетворительным окажется любое решение, если оно соответствует требованиям в полосах пропускания и задерживания.
; поскольку в этой полосе требования не задаются, удовлетворительным окажется любое решение, если оно соответствует требованиям в полосах пропускания и задерживания.
 и
и 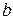 и по ним запишем передаточную характеристику АФ:
и по ним запишем передаточную характеристику АФ:
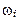 - цифровые частоты;
- цифровые частоты; - аналоговые частоты;
- аналоговые частоты; - период дискретизации
- период дискретизации ;
; ;
; ;
; 
 ;
; ;
;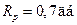 ;
;

 .
.






 .
.



 .
. .
. .
.








 ;
;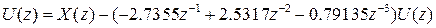 ;
;


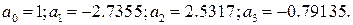


 в виде произведения передаточных функций не выше второго порядка
в виде произведения передаточных функций не выше второго порядка
 .
. получим используя функцию MatLab - tf2sos.
получим используя функцию MatLab - tf2sos. .
.
 Построим частотные характеристики ЦФ и сравним их с аналогичными характеристиками АФ :
Построим частотные характеристики ЦФ и сравним их с аналогичными характеристиками АФ : , где
, где  - коэффициенты передаточной функции. Возвращает АФЧХ и вектор ω круговых частот в радианах. Для расчета АП используется функция
- коэффициенты передаточной функции. Возвращает АФЧХ и вектор ω круговых частот в радианах. Для расчета АП используется функция 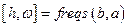 .
.




 Из масштабированной ЛАЧХ видно что полосы пропускания и задержки удовлетворяют заданным требованиям.
Из масштабированной ЛАЧХ видно что полосы пропускания и задержки удовлетворяют заданным требованиям. . Переход к псевдочастоте основан на переходе от
. Переход к псевдочастоте основан на переходе от  - преобразования к
- преобразования к  - преобразованию с помощью подстановки:
- преобразованию с помощью подстановки:
 При этом реальная частота
При этом реальная частота  и псевдочастота
и псевдочастота 
 , она приближенно равна угловой частоте. Нетрудно убедится, что при изменении частоты в диапазоне
, она приближенно равна угловой частоте. Нетрудно убедится, что при изменении частоты в диапазоне 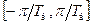 псевдочастота принимает значение бесконечности.
псевдочастота принимает значение бесконечности. мпульсной системы
мпульсной системы  к частотной
к частотной  следует сделать замену
следует сделать замену 


 При этом приведем основные характеристики фильтра.
При этом приведем основные характеристики фильтра.



 Переходная характеристика
Переходная характеристика

 Matlab-программа синтеза БИХ-фильтра
Matlab-программа синтеза БИХ-фильтра


