 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| и расходные характеристики для новых водопроводных труб
| Диаметр, мм | Предельные расходы, л/с | Расходная характеристика К, л/с | Диаметр, мм | Предельные расходы, л/с | Расходная характеристика К, л/с | | - | 9,9 | | | | | - | 28,7 | | | | | до 5,4 | 61,4 | | 130-168 | 4259,3 | | 5,4-9,0 | 110,8 | | 168-237 | 4324,2 | | 9,0-15,0 | 179,4 | | 237-355 | 6999,3 | | 15,0-28,5 | 383,7 | | 355-490 | | | 28,5-45,0 | 692,1 | | 490-685 | | | 45-68 | 1120,6 | | 685-882 | | | 68-96 | 1684,2 | | 882-1120 | | | 96-130 | | | | | б) для принятых диаметров труб по справочной таблице находим расходные характеристики  ; ; в) определяем потери напора на трение для каждого участка по формуле 
г) требуемую высоту водонапорной башни определяем из уравнения Бернулли, написанного для пунктов 1 и 4: 
Так как местность по условию задачи горизонтальная, то  Пьезометрическая высота в первом пункте 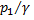 представляет собой искомую высоту водонапорной башни представляет собой искомую высоту водонапорной башни  , а пьезометрическая высота , а пьезометрическая высота  – свободный напор в конечном пункте – свободный напор в конечном пункте  : : 

Округленно принимаем  Определяем пьезометрические высоты в узлах магистрали: 


Таблица 2 – Результаты расчета магистрали | Номера пунктов | Длины участков  , , 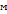 | Расчетные расходы  , ,  | Диаметры труб  , ,  | Расходные характеристики  , ,  | Потери напора  , , 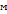 | Пьезометрические высоты  , , 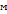 | | | | | | 1120,6 | 0,73 | 16,00 15,27 |
Окончание табл.2 | Номера пунктов | Длины участков  , , 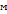 | Расчетные расходы  , ,  | Диаметры труб  , ,  | Расходные характеристики  , ,  | Потери напора  , , 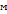 | Пьезометрические высоты  , , 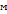 | | | | | | 692,1 383,7 | 0,86 2,3 | 15,27 14,41 12,11 | 4. Ответвления от магистрали делятся на простые и сложные. Простые ответвления состоят из одного участка, а сложные – из двух и более участков. В качестве сложного ответвления в нашем случае выбирается линия 2-5-7, так как участок 5-7 по длине больше, и расход  больше расхода больше расхода  . . Расчет сложного ответвления ведется в определенной последовательности: а) определяем допустимые потери напора для ответвления 2-5-7 как разность пьезометрических высот в начальном и конечном пунктах ответвления: 
б) находим средний гидравлический уклон 
в) определяем требуемые расходные характеристики: 

г) по справочным таблицам в соответствии со значениями требуемых расходных характеристик устанавливаем ближайшие диаметры стандартных труб:  при при  ; ;
 при при  ; ;
д) определяем фактические потери напора для принятых труб 

е) находим пьезометрические высоты 

5. Расчет простых ответвлений 3-8 и 5-6 ведем в ниже излагаемой последовательности и результаты заносим в табл. 3: Таблица 3 – Результаты расчета ответвлений | Номера ответвлений | Длина, м | Расход, л/с | Пьезометрическая высота в начале ответвления, м | Свободный напор в конце ответвления, м | Допустимые потери напора, м | Гидравлический уклон | Требуемая расходная характеристика Ктр, л/с | Диаметр трубы, мм | Расходная характеристика К, л/с | Фактические потери напора, м | Фактический свободный напор в конце ответвления | | 3-8 | | | | | | | | | | | | | 5-6 | | | | | | | | | | | |
а) определяем допустимые потери напора как разность пьезометрических высот в начальном и конечном пунктах 
б) гидравлический уклон 
в) требуемая расходная характеристика 
г) по справочной таблице устанавливаем ближайший больший диаметр стандартной трубы и его расходную характеристику  ; ; д) фактические потери напора 
е) фактический свободный напор в конце ответвления 
 | | Рис. 5 | Задача 6. Определить расход воды  , протекающий из верхнего в нижний резервуар по системе труб, показанной на схеме (рис.5). Разность уровней воды в баках , протекающий из верхнего в нижний резервуар по системе труб, показанной на схеме (рис.5). Разность уровней воды в баках  . Диаметр труб . Диаметр труб  , ,  , ,  , ,  , ,  . Длины труб . Длины труб  , ,  , ,  , ,  , ,  . При решении надо воспользоваться значениями расходных характеристик для новых водопроводных труб (табл.1). . При решении надо воспользоваться значениями расходных характеристик для новых водопроводных труб (табл.1). Решение задачи: Примем  ; ;  ; ;  ; ;  ; ;  ; ;  ; ;  ; ;  ; ;  ; ; 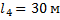 ; ;  . . Рассматривая поток из верхнего в нижний резервуар по трубам 1, 2 и 5, можно записать  . .
Выразив потери напора для отдельных труб через их расходы, длины и расходные характеристики, будем иметь 
Так как потери напора в ветвях замкнутого трубопровода с общими узлами равны между собой, можно составить уравнения  и и 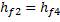
или 
откуда  и и  . .
Общий расход  равен сумме расходов в ветвях замкнутой части системы равен сумме расходов в ветвях замкнутой части системы  . .
Подставим в последнее равенство полученные значения для  и и  , выраженные через , выраженные через  : : 
откуда 
После подстановки последнего значения для  в уравнение для суммарной потери напора в системе будем иметь в уравнение для суммарной потери напора в системе будем иметь 
откуда 
Расходные характеристики для известных диаметров труб устанавливаем по табл.1:  , ,  , ,  , ,  . Значения всех величин подставляем в формулу в дециметрах: . Значения всех величин подставляем в формулу в дециметрах: 

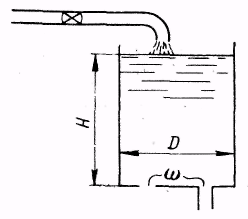 | | Рис. 6 | Задача 7. Цилиндрический бак диаметром  имеет в дне два одинаковых отверстия, одно из которых снабжено внешним цилиндрическим насадком (рис.6). Какой диаметр должны иметь отверстия, чтобы при поступлении в бак расхода воды имеет в дне два одинаковых отверстия, одно из которых снабжено внешним цилиндрическим насадком (рис.6). Какой диаметр должны иметь отверстия, чтобы при поступлении в бак расхода воды  уровень поддерживался на высоте уровень поддерживался на высоте  ? Определить, за какое время ? Определить, за какое время  произойдет опорожнение сосуда через цилиндрический насадок после прекращения притока воды в бак. произойдет опорожнение сосуда через цилиндрический насадок после прекращения притока воды в бак. Решение задачи: Примем  , ,  , ,  . . Расход воды через отверстие  . .
Расход воды через насадок  . .
Общий расход воды  , ,
откуда 
Коэффициент расхода для отверстия  . То же, для цилиндрического насадка . То же, для цилиндрического насадка  . . 
Диаметр отверстий 
Время опорожнения сосуда через цилиндрический насадок 
где  – площадь днища бака – площадь днища бака  Задача 8.На водопроводной трубе диаметром  установлен водомер диаметром установлен водомер диаметром  (рис.7). На какую высоту (рис.7). На какую высоту  поднимается вода в пьезометрической трубке, присоединенной к суженному сечению, при пропуске расхода поднимается вода в пьезометрической трубке, присоединенной к суженному сечению, при пропуске расхода  , если уровень воды в пьезометре, присоединенном к трубе, , если уровень воды в пьезометре, присоединенном к трубе, 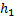 ? Потери напора не учитывать. ? Потери напора не учитывать. Задача 9.По трубопроводу, имеющему сужение, протекает расход воды  . Определить диаметр суженной части трубопровода . Определить диаметр суженной части трубопровода  , если известны показания пьезометров , если известны показания пьезометров 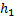 , ,  и диаметр трубопровода и диаметр трубопровода  . Потери напора не учитывать (рис.7). . Потери напора не учитывать (рис.7). Задача 10. На какую высоту  может засасываться вода из резервуара по трубке, присоединенной к узкому сечению трубопровода, если по нему протекает расход может засасываться вода из резервуара по трубке, присоединенной к узкому сечению трубопровода, если по нему протекает расход  (рис.8)? Диаметры (рис.8)? Диаметры  , ,  , избыточное давление в первом сечении , избыточное давление в первом сечении  . Потери напора не учитывать. . Потери напора не учитывать. Задача 11. По трубопроводу, имеющему сужение, протекает расход воды  . Без учета потерь напора определить, какой диаметр . Без учета потерь напора определить, какой диаметр  должна иметь узкая часть трубопровода, чтобы обеспечить засасывание воды из резервуара на высоту должна иметь узкая часть трубопровода, чтобы обеспечить засасывание воды из резервуара на высоту  (рис.8). Диаметр трубопровода (рис.8). Диаметр трубопровода  , вакуумметрическое давление во втором сечении , вакуумметрическое давление во втором сечении  . . Задача 12. К трубопроводу переменного сечения присоединены два пьезометра (рис.9). Пренебрегая потерями напора, определить, на какую высоту  поднимется вода во втором пьезометре, если высота воды в первом пьезометре поднимется вода во втором пьезометре, если высота воды в первом пьезометре 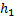 , диаметры , диаметры  , ,  . По трубопроводу протекает расход воды . По трубопроводу протекает расход воды  . . Задача 13. Определить расход воды в горизонтальном трубопроводе переменного сечения (рис. 10), скорость на каждом из его участков и построить пьезометрическую линию, если  , ,  , ,  и и 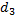 . .  |  | | Рис. 10. | Рис. 11. | Задача 14. Определить расход воды в трубопроводе длиной 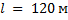 (рис. 11), построить пьезометрическую и напорную линии, если длина первого участка (рис. 11), построить пьезометрическую и напорную линии, если длина первого участка  , его диаметр , его диаметр  , диаметр второго участка , диаметр второго участка  , напор в баке , напор в баке  , отметка начала трубопровода , отметка начала трубопровода  , отметка конца , отметка конца 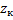 , гидравлические коэффициенты трения , гидравлические коэффициенты трения  , ,  . . Задача 15. Из одного резервуара в другой вода поступает по сифонному трубопроводу длиной  и диаметром и диаметром  (рис.12). Определить расход воды (рис.12). Определить расход воды  при разности уровней в резервуарах при разности уровней в резервуарах  . Трубопровод снабжен приемным клапаном с сеткой ( . Трубопровод снабжен приемным клапаном с сеткой (  ) и задвижкой ( ) и задвижкой (  ). Потерями напора в коленах и на выход из трубы пренебречь. Коэффициент сопротивления трения ). Потерями напора в коленах и на выход из трубы пренебречь. Коэффициент сопротивления трения  . Найти вакуум в опасной точке сифона, если длина участка трубопровода до этой точки . Найти вакуум в опасной точке сифона, если длина участка трубопровода до этой точки  и ее возвышения над уровнем воды в верхнем резервуаре и ее возвышения над уровнем воды в верхнем резервуаре  . . Задача 16.По сифонному трубопроводу длиной  и диаметром и диаметром  нужно обеспечить расход бензина нужно обеспечить расход бензина  . Определить необходимую разность уровней в резервуарах . Определить необходимую разность уровней в резервуарах  и вакуум и вакуум  в опасной точке сифона С, если длина участка трубопровода до этой точки в опасной точке сифона С, если длина участка трубопровода до этой точки  , а ее возвышение над уровнем в верхнем резервуаре , а ее возвышение над уровнем в верхнем резервуаре  (рис.12). Трубопровод имеет приемный клапан с сеткой ( (рис.12). Трубопровод имеет приемный клапан с сеткой (  ) и задвижку ( ) и задвижку (  ). Потери на поворотах не учитывать. Коэффициент сопротивления трения ). Потери на поворотах не учитывать. Коэффициент сопротивления трения  . Объемный вес бензина . Объемный вес бензина  . . Задача 17. Определить максимально допустимую высоту установки насоса  над уровнем воды в бассейне (рис.13) при следующих данных: производительность насоса над уровнем воды в бассейне (рис.13) при следующих данных: производительность насоса  ; вакуум во всасывающем патрубке ; вакуум во всасывающем патрубке  ; длина всасывающей трубы ; длина всасывающей трубы  , диаметр , диаметр  . Всасывающая труба снабжена приемным клапаном с сеткой ( . Всасывающая труба снабжена приемным клапаном с сеткой (  ) и имеет одно сварное колено ( ) и имеет одно сварное колено (  ). Коэффициент сопротивления трения определить по эквивалентной шероховатости ). Коэффициент сопротивления трения определить по эквивалентной шероховатости  мм, предполагая наличие квадратичной зоны сопротивления. мм, предполагая наличие квадратичной зоны сопротивления. Задача 18. Вода подается из нижнего закрытого бака в верхний открытый бак по вертикальной трубе за счет избыточного давления в нижнем баке  (рис.14). Определить расход воды (рис.14). Определить расход воды  при следующих данных: при следующих данных:  , ,  , ,  . Коэффициент сопротивления трения определить по эквивалентной шероховатости . Коэффициент сопротивления трения определить по эквивалентной шероховатости  мм, предполагая наличие квадратичной зоны сопротивления. Коэффициенты местных сопротивлений: входа в трубу мм, предполагая наличие квадратичной зоны сопротивления. Коэффициенты местных сопротивлений: входа в трубу  ; вентиля ; вентиля  ; выхода из трубы ; выхода из трубы  . . Задача 19. Из нижнего бака с избыточным давлением  по новой стальной трубе подается бензин в верхний бак, на поверхности которого поддерживается вакуум по новой стальной трубе подается бензин в верхний бак, на поверхности которого поддерживается вакуум  (рис.15). Разность уровней в баках (рис.15). Разность уровней в баках  , длина трубы , длина трубы  , диаметр , диаметр  . При каком значении коэффициента сопротивления вентиля . При каком значении коэффициента сопротивления вентиля  будет подаваться расход будет подаваться расход  . Потерями напора на вход в трубу и выход из нее пренебречь. Коэффициент сопротивления трения определить по формуле П.Н. Конакова для гидравлически гладких труб. Объемный вес бензина . Потерями напора на вход в трубу и выход из нее пренебречь. Коэффициент сопротивления трения определить по формуле П.Н. Конакова для гидравлически гладких труб. Объемный вес бензина  , коэффициент кинематической вязкости , коэффициент кинематической вязкости  . . Задача 20.Определить диаметры труб для участков тупиковой водопроводной сети (рис.16) и установить требуемую высоту водонапорной башни в точке 1 для подачи следующих расходов в конечные пункты сети:  , ,  , ,  и и  . Длины участков в метрах указаны на схеме сети. Местность горизонтальная. В конечных пунктах сети должен быть обеспечен свободный напор . Длины участков в метрах указаны на схеме сети. Местность горизонтальная. В конечных пунктах сети должен быть обеспечен свободный напор 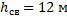 . При расчете воспользоваться значениями предельных расходов и расходных характеристик для новых водопроводных труб (табл. 1). . При расчете воспользоваться значениями предельных расходов и расходных характеристик для новых водопроводных труб (табл. 1). Задача 21. Определить общий расход воды  , поступающий по системе труб под напором , поступающий по системе труб под напором  (рис.17). Диаметры труб (рис.17). Диаметры труб  ; ; 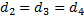 . Длины труб . Длины труб  ; ;  . Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1). . Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1). Задача 22. Определить, при какой разности уровней воды в баках  по системе труб будет протекать расход воды по системе труб будет протекать расход воды  . Диаметры труб . Диаметры труб  , ,  , , 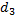 , ,  . Длины труб в метрах указаны на схеме (рис.18). Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1). . Длины труб в метрах указаны на схеме (рис.18). Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1). Задача 23. Определить расход воды, протекающий из верхнего в нижний резервуар по системе труб, показанной на схеме (рис.19). Разность уровней воды в баках  . Диаметры труб (в мм) указаны на схеме. Длины труб . Диаметры труб (в мм) указаны на схеме. Длины труб  , ,  , ,  . Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1). . Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1). Задача 24. Определить, при каком напоре  по системе труб (рис.20) будет протекать расход воды по системе труб (рис.20) будет протекать расход воды  . Диаметры труб . Диаметры труб  , ,  . Длины труб . Длины труб  , ,  . Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1). . Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1). Задача 25. В бак, разделенный тонкой перегородкой на два отсека, поступает расход воды  . В дне каждого отсека имеются одинаковые отверстия диаметром . В дне каждого отсека имеются одинаковые отверстия диаметром  , а в перегородке – отверстие диаметром , а в перегородке – отверстие диаметром 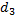 . Определить расходы воды через донные отверстия . Определить расходы воды через донные отверстия  и и  (рис.21). (рис.21). Задача 26. В бак, разделенный тонкой перегородкой на два отсека, поступает расход воды  . В перегородке имеется отверстие диаметром . В перегородке имеется отверстие диаметром  . Из второго отсека вода отливается наружу через цилиндрический насадок диаметром . Из второго отсека вода отливается наружу через цилиндрический насадок диаметром  (рис.22). Определить глубину воды в отсеках над центром отверстий. (рис.22). Определить глубину воды в отсеках над центром отверстий. Задача 27. В баке, имеющем в дне отверстие диаметром  и в стенке отверстие, снабженное цилиндрическим насадком, диаметром и в стенке отверстие, снабженное цилиндрическим насадком, диаметром  , установился уровень воды на высоте , установился уровень воды на высоте  . Определить, какой расход воды . Определить, какой расход воды  поступает в бак, если центр бокового отверстия возвышается над дном бака на высоту поступает в бак, если центр бокового отверстия возвышается над дном бака на высоту  (рис.23). (рис.23). Задача 28. Определить, какой объем воды  был налит в цилиндрический бак диаметром был налит в цилиндрический бак диаметром  , если вся вода вытекла из него через отверстие в дне диаметром , если вся вода вытекла из него через отверстие в дне диаметром  за время за время  (рис.24). Какое время (рис.24). Какое время  потребуется для опорожнения такого же объема воды, если уменьшить диаметр бака в полтора раза? потребуется для опорожнения такого же объема воды, если уменьшить диаметр бака в полтора раза?  |  | | Рис. 24 | Рис. 25 | Задача 29. Призматический бак высотой  с дном площадью с дном площадью  соединен с резервуаром цилиндрическим насадком диаметром соединен с резервуаром цилиндрическим насадком диаметром  (рис.25). Расстояние от дна бака до центра отверстия (рис.25). Расстояние от дна бака до центра отверстия  . Определить, за какое время наполнится бак, если уровень воды в резервуаре не меняется. . Определить, за какое время наполнится бак, если уровень воды в резервуаре не меняется. Задача 30.Как изменится время опорожнения открытого вертикального цилиндрического резервуара диаметром  с начальным напором с начальным напором  , если в его дне внешний коноидальный насадок диаметром , если в его дне внешний коноидальный насадок диаметром  заменить внешним цилиндрическим насадком того же диаметра? заменить внешним цилиндрическим насадком того же диаметра?
ПРИЛОЖЕНИЕ Таблица П1 -Номера контрольных вопросов и задач | Последняя цифра шифра зачетной книжки | Номера задач для студентов очной формы обучения | Номера задач для студентов заочной формы обучения | Номера вопросов для студентов заочной формы обучения | | 8, 13, 15, 20, 22, 25, 28 | 8, 13, 15, 20, 22, 25, 28 | 1, 5, 9, 11, 21 | | 10, 14, 16, 20, 23, 26, 30 | 10, 14, 16, 20, 23, 26, 30 | 2, 4, 8, 10, 20 | | 9, 13, 17, 20, 21, 27, 29 | 9, 13, 17, 20, 21, 27, 29 | 3, 7, 12, 25, 29 | | 11, 14, 19, 20, 23, 27, 29 | 11, 14, 19, 20, 23, 27, 29 | 6, 10, 13, 18, 26 | | 10, 13, 15, 20, 24, 25, 30 | 10, 13, 15, 20, 24, 25, 30 | 1, 14, 16, 19, 27 | | 12, 14, 16, 20, 23, 26, 28 | 12, 14, 16, 20, 23, 26, 28 | 3, 7, 15, 17, 20 | | 8, 13, 19, 20, 22, 27, 29 | 8, 13, 19, 20, 22, 27, 29 | 2, 9, 12, 22, 28 | | 11, 14, 17, 20, 24, 26, 30 | 11, 14, 17, 20, 24, 26, 30 | 4, 8, 17, 23, 30 | | 9, 13, 18, 20, 24, 25, 28 | 9, 13, 18, 20, 24, 25, 28 | 2, 10, 16, 24, 26 | | 12, 14, 18, 20, 21, 26, 29 | 12, 14, 18, 20, 21, 26, 29 | 1, 5, 11, 22, 25 |
Таблица П2 - Числовые значения величин | № задачи | Наименование величины и единицы измерения | Предпоследняя цифра шифра зачетной книжки | | | | | | | | | | | |  , м , м | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 |  , м , м | 0,05 | 0,04 | 0,05 | 0,04 | 0,05 | 0,04 | 0,05 | 0,04 | 0,05 | 0,04 |  , м3/с , м3/с | 0,005 | 0,004 | 0,0045 | 0,005 | 0,004 | 0,0045 | 0,0055 | 0,0035 | 0,006 | 0,003 |  , м , м | 0,8 | 1,4 | 1,0 | 1,2 | 0,7 | 1,3 | 1,1 | 0,9 | 1,0 | 0,8 | |  , м3/с , м3/с | 0,003 | 0,006 | 0,0035 | 0,0055 | 0,0045 | 0,004 | 0,005 | 0,0045 | 0,004 | 0,005 |  , м , м | 0,8 | 1,0 | 0,9 | 1,1 | 1,3 | 0,7 | 1,2 | 1,0 | 1,4 | 0,8 |  , м , м | 0,53 | 0,56 | 0,54 | 0,73 | 0,7 | 0,5 | 0,45 | 0,75 | 0,92 | 0,49 |  , м , м | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 |  10 10 |  , м3/с , м3/с | 0,004 | 0,015 | 0,0045 | 0,0125 | 0,004 | 0,015 | 0,0045 | 0,0125 | 0,004 | 0,015 |  , м , м | 0,06 | 0,10 | 0,06 | 0,10 | 0,06 | 0,10 | 0,06 | 0,10 | 0,06 | 0,10 |  , м , м | 0,025 | 0,04 | 0,025 | 0,04 | 0,025 | 0,04 | 0,025 | 0,04 | 0,025 | 0,04 |  , МПа , МПа | 0,01 | 0,012 | 0,014 | 0,016 | 0,018 | 0,018 | 0,016 | 0,014 | 0,012 | 0,01 | |  , м3/с , м3/с | 0,015 | 0,0045 | 0,0125 | 0,004 | 0,015 | 0,004 | 0,015 | 0,0045 | 0,0125 | 0,004 |  , м , м | 5,2 | 2,5 | 3,5 | 2,1 | 6,0 | 2,3 | 5,8 | 2,7 | 3,3 | 1,5 |  , м , м | 0,10 | 0,06 | 0,10 | 0,06 | 0,10 | 0,06 | 0,10 | 0,06 | 0,10 | 0,06 |  , МПа , МПа | 0,018 | 0,016 | 0,014 | 0,012 | 0,010 | 0,010 | 0,012 | 0,014 | 0,016 | 0,018 | |  , м , м | 0,53 | 0,56 | 0,54 | 0,73 | 0,70 | 0,50 | 0,45 | 0,75 | 0,92 | 0,49 |  , м , м | 0,04 | 0,05 | 0,04 | 0,05 | 0,04 | 0,05 | 0,04 | 0,05 | 0,04 | 0,05 |  , м , м | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 |  , м3/с , м3/с | 0,003 | 0,006 | 0,0035 | 0,0055 | 0,0045 | 0,004 | 0,005 | 0,0045 | 0,004 | 0,005 |
Продолжение прил. 2 | № задачи | Наименование величины и единицы измерения | Предпоследняя цифра шифра зачетной книжки | | | | | | | | | | | |  , м , м | 5,0 | 4,8 | 4,6 | 4,4 | 4,2 | 4,0 | 5,2 | 5,0 | 4,8 | 4,6 |  , м , м | 0,15 | 0,10 | 0,15 | 0,10 | 0,15 | 0,20 | 0,10 | 0,15 | 0,15 | 0,10 |  , м , м | 0,20 | 0,20 | 0,20 | 0,15 | 0,25 | 0,25 | 0,15 | 0,20 | 0,20 | 0,15 |  , м , м | 0,10 | 0,15 | 0,15 | 0,10 | 0,20 | 0,20 | 0,20 | 0,10 | 0,15 | 0,10 |  14 14 |  , м , м | | | | | | | | | | |  , м , м | | | | | | | | | | |  , м , м | 0,10 | 0,095 | 0,09 | 0,10 | 0,095 | 0,09 | 0,10 | 0,095 | 0,09 | 0,09 |  , м , м | 0,15 | 0,14 | 0,13 | 0,12 | 0,15 | 0,14 | 0,13 | 0,12 | 0,14 | 0,12 |  , м , м | 4,5 | 5,0 | 5,5 | 5,0 | 4,5 | 5,0 | 5,5 | 4,5 | 5,0 | 5,5 | 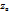 , м , м | | | | | | | | | | |  , м , м | 3,5 | | 3,5 | | 3,5 | | 3,5 | | 3,5 | |  | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 | 0,03 |  | 0,027 | 0,027 | 0,027 | 0,027 | 0,027 | 0,027 | 0,027 | 0,027 | 0,027 | 0,027 | |  , м , м | | | | | | | | | | |  | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 |  , м , м | | | | | | | | | | |  , м , м | | | | | | | | | | |  , м , м | | | | | | | | | | | |  , м , м | | | | | | | | | | |  | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 |  , м3/с , м3/с | 0,0187 | 0,0078 | 0,016 | 0,011 | 0,0171 | 0,0093 | 0,016 | 0,010 | 0,016 | 0,010 |  , м , м | | | | | | | | | | |  , м , м | | | | | | | | | | | Продолжение прил. 2 | № задачи | Наименование величины и единицы измерения | Предпоследняя цифра шифра зачетной книжки | | | | | | | | | | | |  , м3/с , м3/с | 0,030 | 0,015 | 0,045 | 0,015 | 0,045 | 0,030 | 0,045 | 0,030 | 0,015 | 0,030 |  , МПа , МПа | 0,06 | 0,065 | 0,06 | 0,065 | 0,06 | 0,065 | 0,06 | 0,065 | 0,06 | 0,065 |  | | | | | | | | | | |  | 0,20 | 0,15 | 0,25 | 0,15 | 0,25 | 0,20 | 0,25 | 0,20 | 0,15 | 0,20 | |  , МПа , МПа | 0,065 | 0,065 | 0,065 | 0,070 | 0,070 | 0,070 | 0,075 | 0,080 | 0,075 | 0,075 |  | 0,10 | 0,125 | 0,15 | 0,15 | 0,125 | 0,10 | 0,125 | 0,10 | 0,10 | 0,125 |  | | 3,5 | | 3,5 | | | | | 3,5 | |  19 19 |  , МПа , МПа | 0,030 | 0,045 | 0,06 | 0,075 | 0,09 | 0,09 | 0,075 | 0,06 | 0,045 | 0,03 |  , МПа , МПа | 0,060 | 0,045 | 0,03 | 0,03 | 0,015 | 0,03 | 0,015 | 0,045 | 0,03 | 0,075 |  , м , м | | | | | | | | | | |  | | | | | | | | | | |  | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 | 0,075 | 0,10 |  , м3/с , м3/с | 0,018 | 0,030 | 0,016 | 0,040 | 0,020 | 0,040 | 0,020 | 0,035 | 0,016 | 0,035 | | 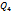 , м3/с , м3/с | 0,022 | 0,024 | 0,026 | 0,028 | 0,030 | 0,030 | 0,022 | 0,028 | 0,024 | 0,026 |  , м3/с , м3/с | 0,006 | 0,008 | 0,010 | 0,008 | 0,010 | 0,006 | 0,010 | 0,006 | 0,008 | 0,008 |  , м3/с , м3/с | 0,010 | 0,006 | 0,008 | 0,008 | 0,006 | 0,
| ©2015 www.megapredmet.ru Все права принадлежат авторам размещенных материалов. |




 ;
;


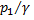 представляет собой искомую высоту водонапорной башни
представляет собой искомую высоту водонапорной башни  , а пьезометрическая высота
, а пьезометрическая высота  – свободный напор в конечном пункте
– свободный напор в конечном пункте  :
:





 ,
, 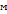
 ,
, 
 ,
, 
 ,
,  ,
,  ,
,  больше расхода
больше расхода  .
.



 при
при  ;
; при
при  ;
;







 , протекающий из верхнего в нижний резервуар по системе труб, показанной на схеме (рис.5). Разность уровней воды в баках
, протекающий из верхнего в нижний резервуар по системе труб, показанной на схеме (рис.5). Разность уровней воды в баках  ,
,  ,
,  ,
,  ,
,  . Длины труб
. Длины труб  ,
,  ,
,  ,
,  ,
,  . При решении надо воспользоваться значениями расходных характеристик для новых водопроводных труб (табл.1).
. При решении надо воспользоваться значениями расходных характеристик для новых водопроводных труб (табл.1). ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 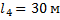 ;
;  .
. .
.
 и
и 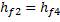

 и
и  .
. .
. и
и  , выраженные через
, выраженные через  :
:



 ,
,  ,
,  ,
,  . Значения всех величин подставляем в формулу в дециметрах:
. Значения всех величин подставляем в формулу в дециметрах:


 имеет в дне два одинаковых отверстия, одно из которых снабжено внешним цилиндрическим насадком (рис.6). Какой диаметр должны иметь отверстия, чтобы при поступлении в бак расхода воды
имеет в дне два одинаковых отверстия, одно из которых снабжено внешним цилиндрическим насадком (рис.6). Какой диаметр должны иметь отверстия, чтобы при поступлении в бак расхода воды  произойдет опорожнение сосуда через цилиндрический насадок после прекращения притока воды в бак.
произойдет опорожнение сосуда через цилиндрический насадок после прекращения притока воды в бак. ,
,  ,
,  .
. .
. .
. ,
,
 . То же, для цилиндрического насадка
. То же, для цилиндрического насадка  .
.


 – площадь днища бака
– площадь днища бака 
 поднимается вода в пьезометрической трубке, присоединенной к суженному сечению, при пропуске расхода
поднимается вода в пьезометрической трубке, присоединенной к суженному сечению, при пропуске расхода 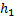 ? Потери напора не учитывать.
? Потери напора не учитывать. может засасываться вода из резервуара по трубке, присоединенной к узкому сечению трубопровода, если по нему протекает расход
может засасываться вода из резервуара по трубке, присоединенной к узкому сечению трубопровода, если по нему протекает расход  . Потери напора не учитывать.
. Потери напора не учитывать. .
.


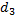 .
.

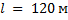 (рис. 11), построить пьезометрическую и напорную линии, если длина первого участка
(рис. 11), построить пьезометрическую и напорную линии, если длина первого участка  , отметка конца
, отметка конца 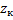 , гидравлические коэффициенты трения
, гидравлические коэффициенты трения  ,
,  .
. и диаметром
и диаметром  (рис.12). Определить расход воды
(рис.12). Определить расход воды  ) и задвижкой (
) и задвижкой (  ). Потерями напора в коленах и на выход из трубы пренебречь. Коэффициент сопротивления трения
). Потерями напора в коленах и на выход из трубы пренебречь. Коэффициент сопротивления трения  . Найти вакуум в опасной точке сифона, если длина участка трубопровода до этой точки
. Найти вакуум в опасной точке сифона, если длина участка трубопровода до этой точки  в опасной точке сифона С, если длина участка трубопровода до этой точки
в опасной точке сифона С, если длина участка трубопровода до этой точки  ) и задвижку (
) и задвижку (  ). Потери на поворотах не учитывать. Коэффициент сопротивления трения
). Потери на поворотах не учитывать. Коэффициент сопротивления трения  . Объемный вес бензина
. Объемный вес бензина  .
. ). Коэффициент сопротивления трения определить по эквивалентной шероховатости
). Коэффициент сопротивления трения определить по эквивалентной шероховатости  мм, предполагая наличие квадратичной зоны сопротивления.
мм, предполагая наличие квадратичной зоны сопротивления. (рис.14). Определить расход воды
(рис.14). Определить расход воды  . Коэффициент сопротивления трения определить по эквивалентной шероховатости
. Коэффициент сопротивления трения определить по эквивалентной шероховатости  ; вентиля
; вентиля  ; выхода из трубы
; выхода из трубы  .
.
 будет подаваться расход
будет подаваться расход  .
. . Длины участков в метрах указаны на схеме сети. Местность горизонтальная. В конечных пунктах сети должен быть обеспечен свободный напор
. Длины участков в метрах указаны на схеме сети. Местность горизонтальная. В конечных пунктах сети должен быть обеспечен свободный напор 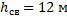 . При расчете воспользоваться значениями предельных расходов и расходных характеристик для новых водопроводных труб (табл. 1).
. При расчете воспользоваться значениями предельных расходов и расходных характеристик для новых водопроводных труб (табл. 1).
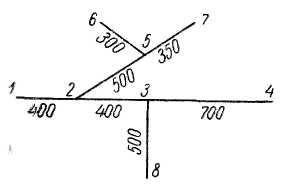
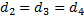 . Длины труб
. Длины труб  . Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1).
. Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1). . Длины труб в метрах указаны на схеме (рис.18). Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1).
. Длины труб в метрах указаны на схеме (рис.18). Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1). . Длины труб
. Длины труб  . Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1).
. Воспользоваться значениями расходных характеристик для новых водопроводных труб (табл. 1).

 , а в перегородке – отверстие диаметром
, а в перегородке – отверстие диаметром  и
и 

 был налит в цилиндрический бак диаметром
был налит в цилиндрический бак диаметром  потребуется для опорожнения такого же объема воды, если уменьшить диаметр бака в полтора раза?
потребуется для опорожнения такого же объема воды, если уменьшить диаметр бака в полтора раза?
 соединен с резервуаром цилиндрическим насадком диаметром
соединен с резервуаром цилиндрическим насадком диаметром  , м
, м , м
, м , м
, м , м
, м 10
10 , МПа
, МПа , м
, м , м
, м , м
, м 14
14 , м
, м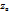 , м
, м , м
, м


 , МПа
, МПа
 , МПа
, МПа
 19
19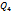 , м3/с
, м3/с , м3/с
, м3/с , м3/с
, м3/с