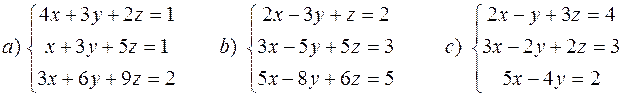ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вектори. Векторнi простори. 12
Черкаський національний університет Ім. Богдана Хмельницького Ілляшенко Н.Г. Лінійна алгебра Частина II Навчально – методичний посібник для організації Черкаси
Посібник містить теоретичні відомості курсу теорії многочленів. Кожен розділ посібника супроводжується набором прикладів розв’язування типових задач. Посібник призначений для організації самостійної роботи студентів стаціонарної та заочної форм навчання.
Рецензент : Атамась В.В. – кандидат фіз-мат наук, доцент кафедри алгебри, геометрії та МВМ ЧНУ ім. Б. Хмельницького. Розділ 1 Системи лiнiйних рівнянь. Питання для самоперевірки: 1. n-мірний числовий вектор-це… 2. Лiнiйним рівнянням називається…, а розв’язком лiнiйного рівняння називається… 3. Системи лiнiйних рівнянь називаються рівносильними, якщо… 4. Чи є система рівнянь лiнiйною а) 5. Чи є вектор (2/3, -1, 3/2, 0) розв’язком рівняння 3x + 4y + 2z - 2t - 1 = 0? 6. Система є сумісно визначеною, якщо… 7. Систему рівнянь записано у векторній формі. Записати її у загальній формі:x(-3,5,0) - y(1,-2,3) + z(1,2,3) = 0 8. Яке з рівнянь системи лiнiйних рівнянь можна викреслити i чому? 9. Чи є система лiнiйних рівнянь сумісною:
10. Елентарнi перетворення СЛР… 11. Теорема Гаусса… 12. Якщо СЛР в результатi елементарних перетворень зводиться до виду трикутника, тo…, а якщо до виду трапеції, то… а) 13. Однорiдною системою лiнiйних рiвнянь називається… 14. Чи завжди СЛОР сумісна? Вiдповiдь пояснити. 15. Сформулювати достатню умову iснування ненульових розв’язкiв СЛОР… 16. Фундаментальна система розв’язкiв – це… 17. Чи є розв’язок (x1, 2x1-x4, 2x4, x4) загальним, а система векторiв a1=(0,-1,2,1),а2=(1,2,0,0) фундаментальною для СЛОР.
18. Вектор b = (b1,b2,…,bn) є розв’язком деякої СЛОР, то вектор kb = (kb1, kb2,…, kbn) є… 19. Якщо b = (b1,b2,…, bn) i c = (c1,c2,…, cn) є розв’язками СЛОР, то вектор b+c є… 20. Що слiдує з умов 19 i 20? 21. Множина розв’язкiв СЛОР утворює… 22. Яка розмiрнiсть простору розв’язкiв однорiдної системи, яка налiчує 7 лiнiйних рiвнянь з 12 змiнними, якщо ранг матрицi системи дорiвнює 5? 23. Система лiнiйних однорiдних рiвнянь називається зведеною, якщо… 24. Зв’язок мiж розв’язками СЛР та вiдповiдної СЛОР… 25. Лiнiйний многовид простору V – це… 26. Розмiрнiстю многовиду називається… 27. Чи є множина розв’язкiв СЛР лiнiйний многовидом?
Задачі: 1. Розв’язати систему лінійних рівнянь: а) c) 2. Розв’язати систему лінійних рівнянь методом Жордана-Гауса: а) c) 3. Знайти загальний і частинний розв’язок системи лінійних рівнянь: а) c) 4. Чи рівносильні дані рівняння і системи лінійних рівнянь: a) 4x + 3y + 2z + 4t = 0 b) 2x + 3y - 4z = 2 c) x+y+2z+8t=0 d) 5x - 3y + z - 8t = 1 5. Дослідити на сумісність і визначеність систему лінійних рівнянь: a) b)
c) 6. Побудувати простір розв’язків системи лінійних однорідних рівнянь: a)
c)
7. Які з рядків матриці А утворюють фундаментальну систему розв’язків для системи лінійних однорідних рівнянь: а) b) 8. Побудувати лінійний многовид для системи рівнянь: а)
c) d) 9. Дослідити систему і знайти загальний розв’язок в залежності від значення параметра
10. Знайти квадратний многочлен f(x), якщо: a) f(1) = -1 f(-1) = 9 f(2) = -3 b) f(1) = 3 f(-1) = 9 f(0) = 5 c) f(1) = 0 f(-1) = 6 f(2) = 3 d) f(1) = 12 f(-1) = 4 f(-2) = 9
Вектори. Векторнi простори.
Питання для самоперевірки: 1. Записати аксiоми векторного простору… 2. Наслiдки iз аксiом векторного простору… 3. Приклади векторних просторiв… 4. Арифметичний векторний простiр – це… 5. Означення пiдпростору… 6. Ознака пiдпростору… 7. З’ясувати чи є множина невироджених матриць другого порядку з елементами з поля R дійсним лiнiйним простором вiдносно операцiй додавання і множення матриць на число? 8. Вектор b є лiнiйною комбінацією векторiв а1,а2,…,аn, якщо… 9. Вказати ознаку лiнiйної залежностi системи векторiв… 10. Записати рiвняння (*) Воно використовується для… 11. Впевнитись в тому, що система векторiв лiнiйно залежна. Виразити один з векторiв через інші: а1 = 1/2, a2 = 3i, a3 = -4-6i. 12. Які з систем векторів є лiнiйно залежними, а якi лiнiйно незалежними: a) а1 = (1,-2,-3), a2 = (2,5,3), a3 = (1/3,2/3,1); b) b1 = (4,1,-2), b2 = (-2,0,1), b3 = (0,0,0); c) c1 = (-17,19,34), c2 = (0,4,5), c3 = (0,0,-24). 13. Розмiрнiсть векторного простору дорiвнює… 14. В n-мiрному векторномиу просторі довільну лiнiйну незалежну систему можна доповнити до … 15. Базис – це… . Ознака базису… 16. Координатами вектора в даному базисi є… 17. Чи є базисом V3 данi системи векторiв: а) а1 = (3,2,1), а2 = (1,3,-2), а3 = (1,1,-6); b) b1 = (1,1,1), b2 = (1,2,1), b3 = (3,4,3). 18. Чи можливо, щоб базис V3 складався з 4 лiнiйно незалежних векторiв, а з 2? Вiдповiдь пояснити. 19. Системою твiрних називається. 20. Ранг системи векторiв – це… 21. Обчислити ранг такої системи векторiв: а1 = (1,0,0,-1), a2 = (2,1,1,0), a3 = (1,1,1,1), a4 = (2,2,2,2), a5= (0,1,2,3). 22. При якому значеннi l система векторiв має ранг 2; 3: a1 = (1,2,3), a2 = (2,4,l), a3 = (-1,3,-2)? 23. Матриця переходу вiд базиса a до базиса a1 називається… 24. Формула зв’язку мiж матрицями в рiзних базисах…
Задачі: 1. З’ясувати лінійно залежною чи лінійно незалежною є система векторів: а) а1 = (1,2,1), a2 = (2,1,2), a3 = (1,2,3) b) a1 = (1,0,1), a2 = (2,3,4), a3 = (1,-3,-3) c) a1 = (1,1,0,1), a2 = (2,1,3,1), a3 = (1,1,0,0), a4 = (0,1,-1,-1) d) A1 = e) a1 = (1,2,-1), a2 = (2,-1,2), a3 = (-7,1,-14) 2. Вектори е1,е2,…,еn, х задані своїми координатами в деякому базисі. Показати, що вектори е1,е2,е3 утворюють базис і знайти координати вектора х в цьому базисі: а) е1 = (2,1,-3), е2 = (3,2,-5), е3 = (1,-1,1), x = (6,2,-7) b) е1 = (1,2,1), е2 = (2,3,3), е3 = (3,1,7), x = (3,3,5) c) е1 = (1,1,1,1), е2 = (1,1,-1,-1), е3 = (1,-1,1,-1), е4 = (1,-1,-1,1), x = (1,2,1,1) d) е1 = (3,1,-3), е2 = (-5,2,1), е3 = (7,3,4), x = (11,12,-1) e) е1 = (1,-7,1), е2 = (2,1,-1), е3 = (5,-5,-1), x = (1,2,3) 3. Розв’язати рівняння: a) 3(a1 - 2x) + 5(a1 + a3-3x) = 2(a3 - 4x), якщо 1) a1 = (4,3), a2 = (2,-1), a3 = (-1,4) 2) a1 = 4+3i, a2 = 2-i, a3 = -1+4i b) 2a1 + 3a2 - a3 - 7x = a4 , якщо a1 = (-1,2,-3,4), a2 = (-1,-1,-1,5), a3 = (2,-5,-1,3), a4 = (2,1,-2,-1) 4. Дано систему векторів a1,…, an. Довести, що вказана підсистема є бизисом даної системи векторів. a) a1 = (1,2,3), a2 = (5,6,7), a3 = (1,1,1), a4 = (2,-1,4), a5 = (2,0,5), a1, a3, a4 b) a1 = (1,2,3,4), a2 = (0,2,3,4), a3 = (0,0,3,4), a4 = (0,0,0,4), a5 = (5,1,4,3), a6 = (7,8,1,9), a7 = (3,3,3,3), a1, a2, a3, a4 c) a1 = (1,1,1,1), a2 = (0,1,0,0), a3 = (0,1,1,0), a4 = (0,1,1,1), a5 = (5,6,7,8), a6 = (8,7,6,5), a7 = (3,3,3,3), a1, a2, a3, a4 d) a1 = (1,2,3,4), a2 = (2,3,4,5), a3 = (3,4,5,6), a4 = (4,5,6,7), a1, a2 e) a1 = (3,1,1,4), a2 = (0,4,10,1), a3 = (1,7,17,3), a4 = (2,2,4,1), a2, a2, a3 5. Обчислити ранг системи векторів в залежності від параметра a) a1 = (2,5,1,3), a2 = (4,6,3,5), a3 = (4,14,1,7), a4 = (2,-3,3, b) b1 = (1, c) a1 = (1,0,-1,2), a2 = (2,-1, d) b1 = ( е) а1 = (3,1,1,4), а2 = ( 6. В просторі С[a,b] візьмемо декілька векторів. а) f1(x) = 1, f2(x) = x, f3(x) = x2, f4(x) = x2 + x + 1. Довести, що система всіх цих векторів лінійно залежна, а будь-які три з цих векторів лінійно незалежні. b) f1(x) = 1 + 2x + 2x2, f2(x) = 2 + 3x + 4x2, f3(x) = 3 + 5x + 7x2 . Довести, що система цих векторів лінійно залежна. c) f1(x) = 1, f2(x) = x, f3(x) = x2, f4(x) = x3. Довести, що система цих векторів утворює базис і знайти координати f(x) = 5 - 2(t+1) + 3(t+1)2 + (t+1)3 в цьому базисі. d) Довести, що система цих векторів лінійно незалежна. Знайти координати Х1, Х2 в цьому базисі. 7. Довести, що а) якщо система векторів a, b, c лінійно незалежна, то система векторів a + b, b + c, c + a також лінійно незалежна b) для якого значення k вектори x = ka + b + 3c, y = ka - 2b + c, z = a – b + c лінійно залежні с) для якого значення k вектори x = ka + 4b + 2c, y = a + 4b + 2c лінійно залежні d) для яких значень k, m вектори x = ka + mb + c, y = a + kb + mc лінійно залежні 8. Знайти k, m, якщо вектори a, b лінійно залежні та a) 3a + 5b = ka + (2m-1)b b) (2k - m - 1)a - (3k - m + 10)b = 0 9. Показати, що вектор 2-7і лінійно виражається через вектори 2-3і, 4+2і.
Матриці. Питання для самоперевірки: 1. Матрицею називається… 2. Транспонування матрицi – це… 3. Яка матриця називається симметричною…, ортогональною…, скалярною…, одиничною… . 4. Для яких матриць iснують одностороннi нейтральнi елементи? Навести приклад. 5. Умова існування добутку матриць… 6. Якi матрицi називаються комутативними? Чи завжди АВ = ВА? Навести приклади комутативних матриць. 7. Умови виконання додавання i множення матриць одночасно… 8. Матриця А¢ називається оберненою до матрицi А, якщо… 9. Необхiдна умова iснування оберненої матрицi… 10. Чи спiвпадають рядковий i стовпчиковий ранги матриць? 11. Елементарнимим перетвореннями матрицi є… 12. Розв’язати матричнi рiвняння: a) XA = B; b) AX = B; c) AXB = C. 13. Чи є матриця А розв’язком рiвняння… X 14. Довести, що коли АВ = ВА, то А-1B = BA-1
Задачі: 1. Обчислити матрицю АВ, якщо а) b) c) 2. Знайти обернену матрицю А-1 для матриці А
3. Розв’язати матричне рівняння:
4. Довести, що коли АВ = ВА, то а) А2 - В2 = (А + В)(А - В) b) (A + B)2 = A2 + 2AB + B2 5. Знайти всі матриці другого порядку, квадрати яких дорівнюють одиничній матриці. 6. Знайти f(А), якщо а) f(x) = x2 - 3x + 2 b) f(x) = c) f(x) = 7. Довести, що 8. Чи утворює множина матриць виду 9. Чи утворює поле множина всіх матриць виду 10. Довести, що матриця 11. Розв’язати систему матричним методом
Детермiнанти. Питання для самоперевірки: 1. Записати правило “трикутника” для обчислення детермiнанта третього порядку… 2. Мiнор – це… 3. Алгебраїчне доповнення елемента – це… 4. Зв’язок мiж Мij i Аij… 5. В якому випадку детермiнант квадратної матрицi дорiвнює нулю? 6. Детермiнант n-го порядку – це… 7. Властивостi детермiнанта n-го порядку… 8. Правило Крамера… 9. Якщо при розв’язуванні СЛР методом Крамера детермiнант головної матрицi дорiвнює нулю і a) всі Dі = 0, то… b) $ Dі ¹ 0, то… 10. Рангом матрицi називається … 11. Теорема про ранг матрицi… 12. Необхiдна i достатня умова iснування оберненої матрицi… 13. Пояснити як за допомогою детермiнанта можна знайти матрицю обернену до даної… 14. Якi з добуткiв належать детермiнанту i якого порядку: a) а21a33a55a42a14; b) a34a25a13a22a55. Вiдповiдь пояснити 15. Якщо в детермiнантi iснує рядок або стовпчик, всi елементи якого дорiвнюють нулю, крiм аij, то… 16. Розкласти детермiнант за елементами i-го рядка або j-го стовпчика означає… 17. Сума всiх попарних добуткiв елементiв довiльного рядка на алгебраїчнi доповнення елементiв другого рядка дорoвнює…
Задачі: 1. Обчислити детермінант, де і =
2. Розв’язати систему лінійних рівнянь методом Крамера
3. Не розкриваючи детермінанта довести, що
4. Розкласти за елементами n-го рядка і обчислити детермінант
5. Обчислити детермінант
6. Обчислити детермінант
7. Розв’язати рівняння
8. Обчислити обернену матрицю за допомогою алгебраїчних доповнень
9. Дослідити на визначеність систему і знайти її загальний розв’язок
10. Обчислити ранг матриці методом окантування мінорів
12 |



 b)
b) 

 b)
b) 

 b)
b) 
 d)
d) 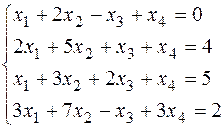


 b)
b) 
 d)
d) 
 b)
b) 
 d)
d) 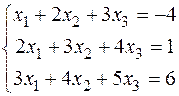






 d)
d) 
 b)
b) 
 d)
d) 




 b)
b) 


 :
:

 A2 =
A2 =  A3 =
A3 =  A4 =
A4 = 
 )
)
 =
=  A=
A= 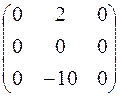














 над полем R групу відносно операції множення матриць?
над полем R групу відносно операції множення матриць? над полем R?
над полем R? задовольняє рівняння
задовольняє рівняння