 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Общий обзор методов вискозиметрии
Таблица.1.1.Исходные данные
Проектирование измерительного преобразователя давления 1.1. Структурная схема. Одним из основных положений современной теории измерительных устройств является положение об измерительном преобразовании. В соответствии с ним измерение рассматривается как процесс приема и преобразования информации об измеряемой величине, происходящий в измерительных устройствах. Структура измерительных устройств, в связи с этим, представляется в виде совокупности измерительных преобразователей, осуществляющих функциональные измерительные преобразования сигналов различной физической природы. Каждый тензорезисторный датчик включает в себя такие измерительные преобразователи, как тензорезистор и измерительная цепь, также тензорезисторные датчики включают в себя упругие элементы, преобразующие усилие или давление в деформацию.
Рис. 1.1. Структурная схема МУЕ - манометрический упругий элемент – (трубка Бурдона); ИУЕ - информационный упругий элемент – (консольная балка балка); МИС – мостовая измерительная схема. На рис. 1.1 представлена структурная схема тензорезисторного датчика давления. Измеряемое давление Рс помощью упругого элемента – трубки Бурдона преобразуется в усилие, а с помощью двухлучевой балки преобразуется в деформацию ε . Деформация упругого элемента воспринимается тензорезистором и преобразуется в изменение сопротивления тензорезистора R, которое в измерительной цепи преобразуется в величину выходного напряжения. По числу изменяющихся под действием измеряемой Эти цепи относятся к цепям прямого преобразования. В соответствии с этой теорией измерительная цепь рассматривается как измерительный преобразователь, характеризуемый функцией преобразования. Входным сигналом в ней является Uпит, а выходным – Uвых. Для данного тензорезисторного преобразователя давления выбираем мостовую измерительную цепь с четырьмя рабочими плечами.
1.2. Принципиальная схема
В данной конструкции в качестве манометрического упругого элемента ис-пользуется трубка Бурдона. Трубка Бурдона 1 под действием давления перемещается на определенную величину
1 – крышка 2 – трубка Бурдона 3 – шарнир 4 – тяга 5 – упругий элемент (консольная балка) 6 – винты 7 – стойка
Рис. 1.2 Принципиальная схема ИПД
Измеряемое давление подается в трубку Бурдона, которая преобразует давление в усилие
Расчет упругого элемента Конструктивные параметры упругого элемента необходимо выбрать исходя из минимизации габаритных размеров ИПД, учитывая пр
Рис.1.3.Трубчатая пружина Бурдона Для определения усилие, возникающего на свободном конце трубки, проведем следующие расчеты: 1. Определим главный параметр пружины:
2. определим коэффициенты При Таблица1.1Зависимость коэффициентов
При
3. Относительный угол поворота конца пружины под действием давления:
4. Полное перемещение конца пружины определяем по формуле:
где
Тогда 5. Радиус поворота
6. Тяговой момент определим по формуле:
7. Определяем усилие, которое создает свободный конец трубки: -радиальное усилие :
-тангенциальное усилие :
Коэффициенты были выбраны из следующего графика:
Рис.1.4.Кривые коэффициентов qr и qτ
Общее усилие:
8. Строим графики трубчатой пружины и балки. Находим точку пересечения графиков, по которой определяем силу, действующую на балку.
Рис.1.5Определения тяговой силы при перемещении λ Теперь пусть Выберем
Эквивалентная схема упругого элемента изображённого на рис 1.6 может быть представлена в виде:
Рис.1.6. Эквивалентная и упрощённая эквивалентная схемы S-образного изгибного УЭ Рассмотрим только одну из двух балок эквивалентной схемы упругого элемента:
Рис. 1.7Расчётная схема консольно защемлённой балки Определим момент заделки Дифференциальное уравнение упругой линии:
В нашем случае это уравнение можно записать в виде:
Проинтегрировав обе части этого уравнения получим:
Поскольку 1. 2. Теперь можем построить эпюру моментов:
Рис. 1.8Эпюра распределения нагружающих моментов Из эпюры видим, что максимальный момент возникает при
Следовательно в этих максимально нагруженных местах и будем клеить тензорезисторы.
Рис. 1.9Схема наклейки и подключения тензорезисторов
Поскольку для балки где: то Откуда
Теперь изобразим эпюру деформаций; для этого вернёмся к уравнению:
Проинтегрировав обе части уравнения получим:
Поскольку
Тогда: Подставляя в последнее выражение числовые значения, получим:
Построив график этой функции в программе MathCad получим упругую линию следующего вида:
1.4.Расчет статической характеристики ИПД: Статическая характеристика – это зависимость выходной в В нашем случае статическую характеристику ИПД для измерительной цепи изображённой на Рис. 3.5 можно записать в следующем виде:
где
где Коэффициент тензочувствительности
где
Тогда номинальное выходное напряжение будет:
Рис 1.11Статическая характеристика ИПД Найдем чувствительность прибора:
1.5.Анализ влияния основных конструктивных пара Будем менять основные конструктивные параметры преобразователя : маленькую полуось b1 и большую полуось a трубки Бурдона, ширины консольной балки b2,толщины стенки трубки Бурдона h1, толщины консольной балки h2, длина консольной балки lв сторону увеличения и в сторону уменьшения относительно номинального (ранее рассчитанного) значения. При этом будем обращать внимание насколько сильно изменение каждого из конструктивных параметров влияет на выходное напряжение.
Рис 1.12Зависимость Uвых от величины маленькой полуоси трубки Бурдона b1.
Рис 1.13Зависимость Uвых от величины ширины консольной балки b2.
Рис 1.14Зависимость Uвых от толщины стенки пружины h1.
Рис 1.15Зависимость Uвых от толщины консольной балки h2.
Рис 1.16Зависимость Uвых от длины консольной балки l.
Рис 1.16.Зависимость Uвых от величины большой полуоси трубки Бурдона а. Исходя из данных приведенных в виде графиков можно сделать вывод что наиболее существенное влияние на статическую характеристику оказывает параметр h2 (высота балки). Следовательно, чтобы повысить чувствительность прибора целесообразно будет уменьшать параметр h2.
Жидкость 1) это тело, обладающее свойством текучести, легкой подвижностью, способное изменять свою форму под воздействием внешних сил и температурных изменений. 2) агрегатное состояние вещества, промежуточное между твёрдым и газообразным состояниями. Жидкость, сохраняя отдельные черты как твёрдого тела, так и газа, обладает, однако, рядом только ей присущих особенностей, из которых наиболее характерная — текучесть. Подобно твёрдому телу, жидкость сохраняет свой объём, имеет свободную поверхность, обладает определённой прочностью на разрыв при всестороннем растяжении и т. д. С другой стороны, взятая в достаточном количестве жидкость принимает форму сосуда, в котором находится. Принципиальная возможность непрерывного перехода жидкости в газ также свидетельствует о близости жидкого и газообразного состояний.
Жидкость, как всякое физическое тело, состоит из отдельных молекул. Молекулы очень малы по сравнению с объемами, рассматриваемыми при изучении жидкости, поэтому в гидравлике не рассматривается молекулярное строение жидкости, предполагая, что жидкость представляет сплошную, непрерывную среду. Жидкости делятся на два вида: капельные и газообразные.
Капельные жидкости — малосжимаемые (вода, нефть, керосин и др.), являются объектом изучения гидравлики и обладают определенным объемом, величина которого практически не изменяется под воздействием внешних сил. Капельные жидкости не всегда заполняют предоставленный им объем, образуя ограниченную поверхность. Например, как указано на рис. 1 , грунтовые воды (являющиеся капельными жидкостями), заключенные в первом от поверхности земли водоносном пласте, подстилаемом водоупором, на какой-то период времени образуют свободную поверхность уровня грунтовых вод Hгр.в. В русле реки А на рис. 1 капельная жидкость для того же времени образует свободную поверхность уровня речных вод Нр. Капельная жидкость может заполнить часть трубы, образуя свободную поверхность, как это представлено на рис. 1. Капельные жидкости обладают капиллярными свойствами. Представим себе, что над свободной поверхностью уровня в порах грунта, вследствие капиллярных свойств капельной жидкости, образуется зона капиллярной каймы. В этом случае может возникнуть необходимость расчета ее высоты и движения воды в данной зоне. Такие вопросы решаются путем гидрогеологических и фильтрационных методов.
рис. 1 а) грунтовые и речные воды б) вода в трубе
Газообразные жидкости занимают все предоставленное им пространство, не имеют свободной поверхности и значительно изменяют свой объем и форму, сжимаясь и расширяясь под воздействием внешних сил. Газообразные жидкости в гидравлике не рассматриваются. Для возможности применения математических решений при изучении жидкости вводится понятие идеальные и реальные жидкости.
Идеальные — невязкие (совершенные) жидкости обладают следующими свойствами: абсолютной подвижностью, т. е. отсутствием сил трения и касательных напряжений; абсолютной неизменностью в объеме под воздействием внешних сил.
Реальные — вязкие (действительные) жидкости обладают: сжимаемостью, сопротивлением растягивающим и сдвигающим усилиям, вязкостью, т. е. возникновением при движении внутреннего трения между частицами. Идеальной жидкости в природе не существует, она является как бы моделью реальной жидкости.
На жидкость, находящуюся в состоянии равновесия или движения, действуют силы: массовые и поверхностные.
Массовые, или объемные, силы пропорциональны массе, а при однородной жидкости и объему. К этим силам относятся: собственная масса жидкости, силы инерции и центробежные силы.
Поверхностные силы пропорциональны площади той поверхности, на которую они действуют. К этим силам относятся: а) силы нормальные к поверхности жидкости (сжатия, давления, растяжения) ; б) касательные (силы трения, возникающие только при движении жидкости).
Рассмотрим свойства жидкости.
1. Плотность жидкости ρ — количество массы (т), содержащееся в единице объема W
2. Сила тяжести
3.Сжимаемость . Капельные жидкости оказывают большое сопротивление сжимающим усилиям и допускают значительное давление. Рассмотрим на рис.2 первоначальный объем жидкости W, м3. Под влиянием давления объем жидкости уменьшится. Вводится коэффициент объемного сжатия ßW, который характеризует уменьшение объема жидкости под влиянием давления
Знак минус показывает, что приращению давления соответствует уменьшение объема жидкости.
рис. 2
Коэффициент объемного сжатия воды зависит от давления и изменяется в незначительных пределах. Так, при изменении давления от 9,81·104 до 2,5·108 Па ßW изменяется от 4,9·10-10 до 2,85·10-10 м2/Н. В гидравлических расчетах ßW принимают постоянным и равным 4,9·10-10 м2/Н.
Модуль упругости воды — величина, обратная коэффициенту объемного сжатия
температурного расширения ßt выражает относительное увеличение объема при повышении температуры на 1°С
где W – первоначальный объем; dW – изменение объема; dt – изменение температуры на 1°С.Размерность ßt в системе СИ 1°С. Значение ßt приведено в таблице. Значение ßt для воды
Следует отметить, что при понижении температуры от +100° до 4°С вода уменьшается в объеме. В интервале от +4°С до 0°С вода не сжимается, а расширяется, имея наибольшую плотность при 4°С. Вода при замерзании увеличивается в объеме приблизительно на 10%.
5. Вязкость жидкости — это свойство жидкости оказывать сопротивление передвижению ее частиц и характеризующее степень ее текучести и подвижности. Как видно из определения, вязкость является свойством движущейся жидкости и в состоянии покоя не обнаруживается. Наличие сил внутреннего трения движущейся жидкости впервые установил Ньютон; впоследствии русский ученый В. Н. Петров в 1888 г. привел математическое выражение для силы трения. Представим на рис.3, что движется поток жидкости в открытом потоке вдоль стенки. Стенка тормозит движение, поэтому скорость будет изменяться по мере удаления от стенки. Рассмотрим два слоя жидкости А к В. Слой А движется со скоростью υ (м/с), слой В — со скоростью υ+ dυ. Расстояние между слоями dy (м), площадь трения F (м2). Градиент скорости
– изменение скорости от одного слоя к другому
рис.3 Введем обозначения: сила внутреннего трения – ТН и μ, динамический коэффициент вязкости Н·с/м2 или Па·с. В принятых обозначениях сила трения имеет вид
Знак минус указывает на то, что трение задерживает движение. Рассмотрим применяемые в гидравлике три единицы вязкости: динамический коэффициент, кинематический коэффициент и относительную вязкость.
Динамический коэффициент вязкости. Из предыдущей формулы определяется динамический коэффициент вязкости
В системе СИ размерность μ выражается в Н·с/м2 или Па·с.
Кинематический коэффициент вязкости v. В гидравлических расчетах применяется вязкость, отнесенная к плотности
где ρ – плотность. Размерность v в системе СИ – м2/с. Вязкость жидкости уменьшается при увеличении температуры. При нормальном атмосферном давлении для определения кинематического коэффициента вязкости воды в зависимости от температуры составлена таблице.
Значение v м2/с для воды в зависимости от температуры
Вязкость жидкости зависит и от давления. При давлении до 2·107 Па изменение вязкости воды незначительно и часто в расчетах не учитывается.
есть относительная вязкость (для глинистых растворов она всегда больше 1).
6. Капиллярность (поверхностное натяжение) – это свойство жидкости изменять положение ее поверхности, вызванное натяжением и силой взаимодействия между нею и стенками трубок или мелкими порами грунта. Поверхностное натяжение зависит от температуры, уменьшаясь с ее ростом. Вода из всех жидкостей имеет наибольшее поверхностное натяжение σt=0,081 Н/м. Для воды при температуре 20°С в трубке диаметром d мм высота капиллярного поднятия выражается формулой
Рис4.Капиллярное поднятие жидкости, смачивающей стенки (вода в стеклянном сосуде и капилляре).
Получившаяся смесь имеет свойства, резко отличающиеся от свойств воды, прежде всего сжимаемость, этой эмульсии резко возрастает. Выделившиеся пузырьки воздуха, и паров уносятся потоком в области повышенного давления, где паровые пузырьки конденсируются, а воздушные пузырьки сжимаются (смыкаются). Такое сжатие воздушного и конденсация парового пузырьков происходит мгновенно и сопровождается значительными мгновенными местными повышениями давлений, в несколько тысяч раз превосходящими атмосферное. В результате ограничивающие поток стенки или части механизмов (насосы, турбины), соприкасающиеся с потоком в тех местах, где конденсируются пузырьки пара, подвергающиеся многократным микроударам, разрушаются. Происходит эрозия материала. Описанное явление называется кавитацией. z:\CorvDoc\sssr5-1\games\Fifa\!!Oleg\Nikitin\Kursach\Nikitin\Temp\Study\Інформ мех (Нікітін)\вязкость\properties.htm - top Общий обзор методов вискозиметрии Вискозиметрия основана на законе вязкости Ньютона. Из него следует, что для определения вязкости необходимо измерить напряжение, которое сообщает слою жидкости некоторую скорость по отношению к другому слою, находящемуся от первого слоя на определенном расстоянии. На практике удобнее задавать постоянное напряжение и наблюдать скорость относительного движения. При этом можно определять скорость движения жидкости по отношению к неподвижному твердому телу или скорость движения твердого тела
в неподвижной жидкости. Оба эти принципа нашли применение при конструировании вискозиметров. Приборы с неподвижными стенками представлены капиллярными вискозиметрами. Примером второго типа вискозиметров могут служить приборы с падающим шариком.
В восьмидесятых годах прошлого столетия Ф. Н. Шведов [3] разработал оригинальный метод определения реологических параметров дисперсных систем по закручиванию цилиндра, подвешенного на упругой нити и погруженного в жидкость. Прибор Шведова был одним из первых вискозиметров с коаксиальными цилиндрами. В последнее время этот прибор усовершенствован в лаборатории П. А. Ребиндера. Возникновение нефтяной вискозиметрии связано с именем Н. П. Пет- юва [2]. В конце прошлого столетия он провел обширные и очень тщательные измерения вязкости ряда минеральных и растительных масел с помощью сконструированного им капиллярного прибора (рис. 6). В это же время С. Ламанский [4] предложил специальный вискозиметр для масел, имеющий ряд преимуществ по сравнению с появившимся позднее вискозиметром Энглера.
Рис.5. Прибор Ломоносова для определения вязкости жидкости (1752 г.)
Рис. 6. Схема капиллярного вискозиметра Н. П. Петрова.
Невозможно создать универсальные вискозиметры или пластометры, одинаково пригодные для всех случаев. По принципиальным особенностям конструкции приборы для измерения вязкости делятся на следующие типы: 1) капиллярные вискозиметры; 2) ротационные вискозиметры, или приборы с коаксиальными цилиндрами; 3) вискозиметры с падающим шариком; 4) маятниковые вискозиметры; 5) вискозиметры с взаимно смещающимися цилиндрами или пластинками; 6) приборы, основанные на принципе сдувания тонкого слоя жидкости; 7) вискозиметры, основанные на других принципах. Наиболее распространены капиллярные вискозиметры. Поданным М. П. Воларовича [5], около 80% всех измерений вязкости производится с их помощью. Эти приборы отличаются простотой, требуют малого количества жидкости, дешевы и дают достаточно точные результаты. К числу их недостатков относится невозможность измерения вязкости очень вязких жидкостей. Второе место занимают ротационные вискозиметры. Эти приборы обеспечивают однородное поле напряжения в жидкости и позволяют измерять вязкость с высокой точностью. Сложность конструкции ротационных вискозиметров ограничивает их применение. К недостаткам их следует также отнести накопление в деформируемой жидкости диссипированного тепла. В капиллярных приборах это тепло уносится вместе с протекающей жидкостью.
К простым приборам относятся также вискозиметры с падающим шариком, но с их помощью можно получить хорошие результаты только у вязких и вполне однородных жидкостей. Для измерения пластичности и вообще реологических свойств веществ, наряду с вязкостью необходимо определять предельные напряжения сдвига и модули упругости. Принципиально такие измерения могут производиться в вискозиметрах всех перечисленных групп, но в то время как при вискозиметрии измеряют значительные деформации (например, протекание всего исследуемого объема)жидкости через капилляр), при определении модуля упругости и предельного напряжения сдвига наблюдают малые деформации. Для измерений малых деформаций более удобны вискозиметры с взаимно смещающимися цилиндрами или пластинками и ротационные вискозиметры. Если при определении вязкости жидкостей наблюдают только скорость деформации при постоянном напряжении, то при изучении пластичных тел измеряют также силу, вызывающую начало течения, и размер деформации при различных нагрузках ниже предела текучести. Отличие пластометров от вискозиметров заключается в том, что первые снабжены приспособлениями для варьирования напряжения. Вискозиметры для исследования аномалии вязкости имеют устройства для изменения скорости течения жидкости (в частности, капиллярные вискозиметры — установки для изменения разности давлении на концах капилляра). В нефтяной вискозиметрии капиллярные приборы являются основным типом вискозиметров для светлых нефтепродуктов и минеральных масел при положительных температурах. При низких температурах для масел применяют как капиллярные, так и ротационные вискозиметры. М. П. Врларович [17] считает, что для моторных масел Капиллярные вискозиметры могут применяться лишь до -10 ÷ 20°, так как при более низких температурах масла обладают слишком высокой вязкостью .для приборов этого типа. В. Л. Вальдман и A. М. Фомина [16] нашли, что масла с вязкостью Е50 = 12—20 можно исследовать в капиллярном вискозиметре Пинкевича до -15° и масла с Е50 = 5—10 до —30°. Эти авторы установили также, что для масел с Е50 < 6° кривые Для изучения консистентных смазок и битумов пользуются преимущественно приборами со смещающимися цилиндрами и пластинками, ротационными вискозиметрами и вискозиметрами с падающими шариками. В последнее время Г. В. Виноградов и В. П. Павлов [18] сконструировали капиллярный вискозиметр для консистентных смазок. Кроме физически обоснованных вискозиметров, в нефтяных лабораториях сохранились вискозиметры, устройство которых основано на условных
Сложность реологических свойств смазок, масел и топлив при низких температурах, а также недостатки условных технических вискозиметров и пластометров привели к тому, что для оценки механических свойств этих нефтепродуктов в условиях эксплуатации были предложены специальные приборы, представляющие собой модели масляных систем двигателей или других механизмов или непосредственно части этих систем. К ним относятся приборы В. К. Лимаря и В. Г. Сидорова [6], К. С. Рамайя [7] и В. В. Соколова [8] для определения прокачиваемости масел при низких температурах, установка Д. Л. Гольдштейна, 3. В. Векслера и Г. Е. Журавлева [9] для определения нижнего температурного предела эксплуатации дизельных топлив и кинематические пары поршень-цилиндр и вал-подшипник, применявшиеся М. П. Вола-ровичем [19, 20] для исследования минеральных масел при низких температурах. Вискозиметры, позволяющие измерять вязкость в абсолютных единицах (пуазах и стоксах), делятся на первичные и вторичные. В первичных вискозиметрах весьма точно определяются размеры прибора, объем протекшей жидкости и напряжение. Они служат для измерения вязкости первичных (калибровочных) жидкостей и для весьма точных измерений вязкости остальных жидкостей. Абсолютные вискозиметры довольно сложны по устройству и применяются главным образом для специальных физико-хими|ческих исследований. Для практических целей пользуются вторичными вискозиметрами, в которых вязкость измеряется путем сравнения скорости течения испытуемой жидкости с эталонной, вязкость которой измерена в первичном вискозиметре. Основными калибровочными жидкостями служат вода, касторовое масло, раствор сахара в воде, некоторые индивидуальные органические соединения и минеральные масла.
1. Типы капиллярных вискозиметров. Капиллярные вискозиметры состоят из трех основных частей: резервуара для испытуемой жидкости, тонкой трубки-капилляра и приемника для жидкости после капилляра. Напряжение, обусловливающее течение жидкости, зависит от радиуса и длины капилляра и разности давления, приложенной к его концам. Источником давления служит вес столба испытуемой жидкости в приборе (гидростатическое давление) или внешнее давление, подаваемое на мениск жидкости в вискозиметре, или сочетание обоих видов давления. Во многих случаях капиллярные вискозиметры выполняются в виде стеклянной U-образной трубки, в одно колено которой впаяны резервуар (расширение с мешками на концах) и капилляр, а в другое - приемник. Распространены также пипеточные вискозиметры. У этих приборов капилляр введен в нижнюю трубку пипетки, а расширение является резервуаром. Приемники пипеточных вискозиметров имеют разнообразную форму. Эти приборы не имеют каких-либо существенных преимуществ перед U-образ-ными вискозиметрами, а некоторые из них (например, вискозиметр Барра —английский стандартный вискозиметр) сложны в изготовлении. В зависимости от положения капилляра различают вискозиметры с вертикальными, горизонтальными и наклонными капиллярами. Более распространены первые, так как они отличаются компактностью и удобны для термостатирования. Однако многие вискозиметры для точных измерений вязкости маловязких жидкостей и жидкостей, обладающих аномалией вязкости, имеют горизонтальные капилляры. Измерение вязкости в капиллярных приборах основано на формуле Пуазейля, связывающей вязкость с расходом продукта. В большинстве вискозиметров расход измеряется по времени истечения определенного объема жидкости из резервуара через капилляр в приемник. Реже измеряют объем вытекающей жидкости за единицу времени. Особую группу капиллярных приборов составляют вискозиметры постоянного расхода, в которых задается расход и измеряется соответствующее ему давление. Последние приборы применяют для вискозиметрических исследований пластичных тел [12], в частности консистентных смазок [13, 18]. Капиллярные вискозиметры с постоянным давлением, как правило, выполняются из стекла, капиллярные вискозиметры постоянного расхода —из металла и стекла.
Рис.7 Капилярные вязкозиметры
Ротационные вискозиметры Ротационные вискозиметры или вискозиметры с коаксиальными цилиндрами состоят из двух соосных вертикальных цилиндров, между которыми помещается испытуемая жидкость. Электромотором или падающим грузом один из цилиндров приводится во вращение. Исследуемая жидкость оказывает вязкое сопротивление его вращению и передает движение второму цилиндру. У некоторых типов приборов вращается внутренний цилиндр, а у других — внешний. В зависимости от способа монтирования второго цилиндра ротационные
В приборах с одним неподвижным цилиндром вязкость испытуемой жидкости определяется по скорости вращения подвижного цилиндра при заданном крутящем моменте или по величине крутящего момента, вызывающего заданную скорость. Вязкость вычисляется по формуле
где К — постоянная прибора; М = rt — крутящий момент; Ω— угловая скорость. У торсионных вискозиметров внутренний цилиндр подвешен на упругой нити. Движение жидкости вызывает закручивание цилиндра на угол, при котором момент упругих сил, возникающих при закручивании нити, уравновешивается моментом сил внутреннего трения вращающейся жидкости. Угол поворота цилиндра φизмеряется. Если Ω — угловая скорость вращения внешнего цилиндра; К—постоянная для подвеса, зависящая от его упругости; С —постоянная вискозиметра, определяющаяся геометрическими размерами прибора, то вязкость испытуемой жидкости вычисляется по формуле:
Постоянные ротационных вискозиметров определяются обмером или калиброванием эталонными жидкостями. Как правило, ротационные вискозиметры выполняются из металла. Важным условием точных и воспроизводимых измерений вязкости является постоянное и возможно меньшее трение цилиндров и других движущихся деталей в опорах. Вращающийся цилиндр устанавливается на шариковых подшипниках. Для устранения скольжения испытуемого материала по стенкам цилиндров внутренние их поверхности иногда делают ребристыми, либо с продольной насечкой. Наибольшие трудности при изготовлении и применении ротационных | вискозиметров возникают вследствие необходимости вносить поправки на дно внутреннего цилиндра. Самый простой, но недостаточно точный способ заключается в том, что дно цилиндра делают слегка вогнутым. При погружении цилиндра в жидкость в вогнутости остается воздух и трение дна уменьшается. Отдельные авторы помещали под дно внутреннего цилиндра маловязкую жидкость, например ртуть. Куэтт [47] и Гатчек [48, 55] монтировали внутренний цилиндр между специальными охранными кольцами, уменьшающими турбулентность от его концов. М. П. Воларович [46] пользовался длинными и узкими цилиндрами, чтобы относительная ошибка от трения дна была невелика. В других своих приборах он применял сферическое дно [53]. Теория трения
А. Ф. Добрянский, А. П. Сиверцев и И. Я. Фридман [60] применили для исследования вязкости минеральных масел при низких температурах i прибор с очень малым зазором между цилиндрами, что позволило не заполнять дна прибора жидкостью и тем самым исключить поправки на дно. Аналогичный принцип использован Заалем и Коэнсом [59] в приборе для исследования битумов. s Следует, однако, отметить, что ошибки от краевых эффектов у вторичных ротационных вискозиметров с длинными и узкими цилиндрами не оказывают значительного влияния на измерения вязкости высоковязких веществ, но они снижают скорости, при которых соблюдается пропорциональность между крутящим моментом и угловой скоростью или угловой скоростью и углом закручивания цилиндра. Таким образом, дефекты прибора сокращают ламинарную область течения. Специфический недостаток торсионных вискозиметров заключается в остаточной неупругой деформации, присущей нити подвеса. Плавленый кварц является наиболее подходящим материалом для нити, так как обладает высокой и постоянной упругостью, но эти свойства присущи ему только в тонких нитях. Поэтому кварцевые подвесы применяются лишь для небольших цилиндров. Для тяжелых цилиндров используется стальная проволока и проволока из фосфористой бронзы. М. П. Воларович разработал несколько модификаций ротационных вискозиметров с неподвижным цилиндром [46, 52, 53]. Наиболее совершенным является вискозиметр РВ-7 с неподвижным внешним цилиндром [52, 53]. Этот прибор рекомендуется М. П. Воларовичем для определения динамической вязкости минеральных масел при температурах от +10° до—60°, дизельных топлив при температурах ниже —30° и битумов при температурах от +20° до +160°. Измерения вязкости могут производиться в пределвх от 5 до Схема вискозиметра представлена на Рис. 8. Прибор состоит из внешнего неподвижного цилиндра 2 и внутреннего вращающегося цилиндра 1, приводящегося в движение падающими грузами, привешенными к двум нитям (одна нить на схеме не показана), намотанными на шкив 6. Прибор снабжен хорошей термоизоляцией 16. В пространство между нею и внешним цилиндром
Рис. 8. Ротационный вискозиметр РВ-7.
помещается охлаждающая смесь или термостатная жидкость, В термостат вмонтирован электрический нагреватель, позволяющий поднимать температуру до 160°. Для измерения температуры служат три термопары 14, вмонтированные в наружный цилиндр. При измерении вязкости определяется время вращения внутреннего цилиндра с помощью стрелки Р и шкалы 10. Вязкость в пуазах вычисляется по следующей формуле:
где Р— вес груза, вращающий цилиндр вискозиметра, равный сумме весов двух грузов, подвешенных к обеим нитям прибора; Р0 — собственное трение подшипников (оно может быть снижено до 1—2 г); N— число оборотов цилиндра в секунду; К — постоянная прибора, зависящая от его размеров и высоты уровня испытуемой жидкости (глубины погружения внутреннего цилиндра):
где А, В и С — постоянные для данного прибора; h — глубина погружения цилиндра.
Рис. 9 |









 На рис.1.1 представлена структурная схема измерительного преобразователя давления (ИПД).
На рис.1.1 представлена структурная схема измерительного преобразователя давления (ИПД). величины сопротивлений подразделяют измерительные цепи на цепи с одним рабочим плечом, с двумя рабочими плечами и с четырьмя рабочими плечами.
величины сопротивлений подразделяют измерительные цепи на цепи с одним рабочим плечом, с двумя рабочими плечами и с четырьмя рабочими плечами.
 . Тяга 2, прикрепленная к трубке и жесткому центру 4 двухлучевой балки по средствам шарниров 6, действует на двухлучевую балку 3, защемленную с двух сторон. Балка под действием тяги деформируется, что в свою очередь приводит к изменению выходного напряжения мостовой схемы, состоящей из 4-х тензорезисторов 5, размещенных на двухлучевой балке. На рис.1.3 представлена принципиальная схема измерительного преобразователя давления.
. Тяга 2, прикрепленная к трубке и жесткому центру 4 двухлучевой балки по средствам шарниров 6, действует на двухлучевую балку 3, защемленную с двух сторон. Балка под действием тяги деформируется, что в свою очередь приводит к изменению выходного напряжения мостовой схемы, состоящей из 4-х тензорезисторов 5, размещенных на двухлучевой балке. На рис.1.3 представлена принципиальная схема измерительного преобразователя давления.
 и передаёт это усилие на упругий элемент - консольную балку. Усилие преобразуется в изгибающий момент, который действует в местах наклейки тензорезисто
и передаёт это усилие на упругий элемент - консольную балку. Усилие преобразуется в изгибающий момент, который действует в местах наклейки тензорезисто  ров. Вследствие этого упругий элемент деформируется и одновременно деформирует плотно наклеенные на него тензорезисторы. При этом происходит преобразование изгибающего момента
ров. Вследствие этого упругий элемент деформируется и одновременно деформирует плотно наклеенные на него тензорезисторы. При этом происходит преобразование изгибающего момента  в деформацию поверхностей упругого элемента и соответственно в деформацию тензорезисторов
в деформацию поверхностей упругого элемента и соответственно в деформацию тензорезисторов  , что приводит к изменению их сопротивлений
, что приводит к изменению их сопротивлений  . Изменение сопротивлений тензорезисторов вызывает изменение выходного сигнала измерительной цепи
. Изменение сопротивлений тензорезисторов вызывает изменение выходного сигнала измерительной цепи  , пропорционального входному давлению
, пропорционального входному давлению 
 и этом, что относительная деформация упругого элемента в местах наклейки тензорезисторов
и этом, что относительная деформация упругого элемента в местах наклейки тензорезисторов  Пусть средний радиус трубки Бурдона составляет
Пусть средний радиус трубки Бурдона составляет  , малая и большая полуоси поперечного сечения трубки, которая представляет собой овал
, малая и большая полуоси поперечного сечения трубки, которая представляет собой овал  ,
, 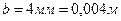 , толщина стенки трубки
, толщина стенки трубки  , угол разворота трубки
, угол разворота трубки  , параметры
, параметры  показаны на рисунке 1.3.
показаны на рисунке 1.3.
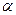 ,
,  и
и 
 для плоскоовальной формы сечения
для плоскоовальной формы сечения  и
и  .
. ,
,  ,
,  от соотношения полуосей сечения.
от соотношения полуосей сечения.


 , вычислим коэффициент по следующей формуле:
, вычислим коэффициент по следующей формуле: 
 (1.1)
(1.1)
 ; (1.2)
; (1.2) .
. ; (1.3)
; (1.3) ; (1.4)
; (1.4) ;
; ; (1.5)
; (1.5) .
. .
. определим как:
определим как: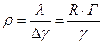 ; (1.6)
; (1.6) ; (1.7)
; (1.7) .
.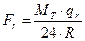 ; (1.8)
; (1.8) ;
; ; (1.9)
; (1.9) .
.
 (1.10)
(1.10)


 ,
,  .
. , таким образом чтобы
, таким образом чтобы 



 :
: ; (1.11)
; (1.11) ; (1.12)
; (1.12) ; (1.13)
; (1.13)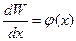 , то с учётом граничных условий можем рассчитать:
, то с учётом граничных условий можем рассчитать: ,
, 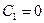 ;
;
 ,
,  ,
,  ;
; ;
; ;
; ,
,  ;
;

 и при
и при 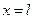 и являются противоположными по знаку но равными по величине
и являются противоположными по знаку но равными по величине  .
.

 ; (1.14)
; (1.14) , (1.15)
, (1.15) ; (1.16)
; (1.16) ; (1.17)
; (1.17)

 ;
;  (1.18)
(1.18) ; (1.19)
; (1.19) , то
, то  ;
;  ; (1.20)
; (1.20) ;
; ;
;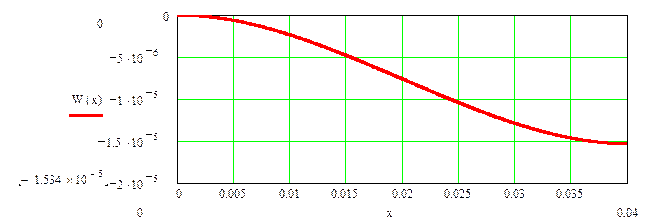 Рис. 1.10Эпюра деформаций УЭ
Рис. 1.10Эпюра деформаций УЭ
 еличины преобразователя от входной величины, при условии, что входное воздействие постоянная величина.
еличины преобразователя от входной величины, при условии, что входное воздействие постоянная величина. ; (1.21)
; (1.21) - коэффициент симметрии цепи
- коэффициент симметрии цепи  ;
;  ;
; ; (1.22)
; (1.22)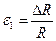 - относительное изменение сопротивления тензорезисторов.
- относительное изменение сопротивления тензорезисторов.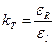 , откуда
, откуда  ;
; ; (1.23)
; (1.23)
 ; (1.25)
; (1.25) ; (1.26)
; (1.26) ; (1.27)
; (1.27)
 ;
; ;
;

 ; (1.28)
; (1.28)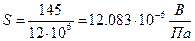 .
. метров ИПД на статическую характеристику преобразователя
метров ИПД на статическую характеристику преобразователя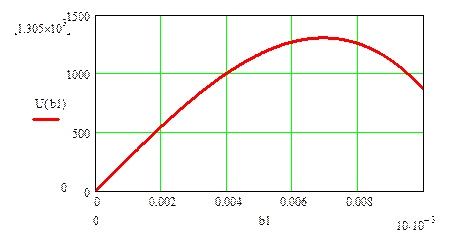







 Вязкость жидкости
Вязкость жидкости

 кг/м3
кг/м3

 Н/м2=Па
Н/м2=Па
 4. Температурное расширение. Жидкие тела при колебании температуры изменяют свой объем и плотность. Коэффициент
4. Температурное расширение. Жидкие тела при колебании температуры изменяют свой объем и плотность. Коэффициент






 Относительная вязкость. Вязкость жидкостей может быть определена вискозиметром. Существует несколько типов таких приборов. В простом полевом вискозиметре, основанном на принципе истечения, в воронку наливается, например, глинистый раствор объемом 500 см3, вязкость которого следует установить. Измеряются температура и время истечения из воронки исследуемого раствора Тр; затем наливается в воронку дистиллированная вода при такой же температуре (обычно 20°С) и определяется время ее истечения Тв. Отношение
Относительная вязкость. Вязкость жидкостей может быть определена вискозиметром. Существует несколько типов таких приборов. В простом полевом вискозиметре, основанном на принципе истечения, в воронку наливается, например, глинистый раствор объемом 500 см3, вязкость которого следует установить. Измеряются температура и время истечения из воронки исследуемого раствора Тр; затем наливается в воронку дистиллированная вода при такой же температуре (обычно 20°С) и определяется время ее истечения Тв. Отношение

 7. Кавитация. В обычных условиях (при нормальном атмосферном давлении и обычной температуре) вода содержит около 2% объема растворенного в ней воздуха. Часть этого воздуха при понижении давления до определенного предела выделяется из воды, при этом образуются и пары жидкости.
7. Кавитация. В обычных условиях (при нормальном атмосферном давлении и обычной температуре) вода содержит около 2% объема растворенного в ней воздуха. Часть этого воздуха при понижении давления до определенного предела выделяется из воды, при этом образуются и пары жидкости. Первый вискозиметр был предложен еще в1752 г. М. В. Ломоносовым [1]. Вязкость в этом приборе (рис.5) измерялась по скорости протекания жидкости через зазор между стенками воронки и вставленным в нее шаром. Величину зазора можно было регулировать, поднимая или опуская шар. Воронка наполнялась до постоянного уровня из специального резервуара, что обеспечивало постоянное гидростатическое давление на жидкость в зазоре, а следовательно, и постоянное напряжение. Скорость течения измерялась числом капель, падающих из воронки за единицу времени. Прибор Ломоносова включал многие основные элементы современных вискозиметров.
Первый вискозиметр был предложен еще в1752 г. М. В. Ломоносовым [1]. Вязкость в этом приборе (рис.5) измерялась по скорости протекания жидкости через зазор между стенками воронки и вставленным в нее шаром. Величину зазора можно было регулировать, поднимая или опуская шар. Воронка наполнялась до постоянного уровня из специального резервуара, что обеспечивало постоянное гидростатическое давление на жидкость в зазоре, а следовательно, и постоянное напряжение. Скорость течения измерялась числом капель, падающих из воронки за единицу времени. Прибор Ломоносова включал многие основные элементы современных вискозиметров.
 В настоящее время число вискозиметров различной конструкции весьма велико, и их количество продолжает расти. Только в нефтяной вискозиметрии применяется или применялось около 200 приборов. Такое значительное число вискозиметров объясняется разнообразием задач вискозиметрии и различием свойств исследуемых жидкостей и пластичных тел.
В настоящее время число вискозиметров различной конструкции весьма велико, и их количество продолжает расти. Только в нефтяной вискозиметрии применяется или применялось около 200 приборов. Такое значительное число вискозиметров объясняется разнообразием задач вискозиметрии и различием свойств исследуемых жидкостей и пластичных тел.
 Ротационные вискозиметры применяются преимущественно для измерения вязкости дисперсных систем и высоковязких жидкостей и дополняют капиллярные приборы.
Ротационные вискозиметры применяются преимущественно для измерения вязкости дисперсных систем и высоковязких жидкостей и дополняют капиллярные приборы. , полученные в капиллярных и ротационных вискозиметрах, совпадают до температур порядка —30°. У масел с вязкостью Е50 = 10—15 вязкость, полученная обоими методами, совпадает до температур порядка —10°.
, полученные в капиллярных и ротационных вискозиметрах, совпадают до температур порядка —30°. У масел с вязкостью Е50 = 10—15 вязкость, полученная обоими методами, совпадает до температур порядка —10°. технических методах оценки реологических свойств. Некоторые из них, как, например, методы определения температуры застывания или каплепадения, предназначены для определения температуры изменения свойств нефтепродуктов. Другие позволяют сравнивать свойства испытуемых веществ с известными или эталонными продуктами. Многие из этих методов страдают существенными дефектами. Так, в вискозиметре Энглера не всегда обеспечивается ламинарное течение, в приборах для определения температуры застывания недостаточно определено напряжение, да и вообще неясно, наблюдается ли предел текучести или высокая вязкость. Одна из наиболее актуальных задач нефтяной вискозиметрии заключается в замене определения вязкости при помощи условных методов определением простыми, физически обоснованными приборами.
технических методах оценки реологических свойств. Некоторые из них, как, например, методы определения температуры застывания или каплепадения, предназначены для определения температуры изменения свойств нефтепродуктов. Другие позволяют сравнивать свойства испытуемых веществ с известными или эталонными продуктами. Многие из этих методов страдают существенными дефектами. Так, в вискозиметре Энглера не всегда обеспечивается ламинарное течение, в приборах для определения температуры застывания недостаточно определено напряжение, да и вообще неясно, наблюдается ли предел текучести или высокая вязкость. Одна из наиболее актуальных задач нефтяной вискозиметрии заключается в замене определения вязкости при помощи условных методов определением простыми, физически обоснованными приборами. 2. Капиллярные вискозиметры
2. Капиллярные вискозиметры


 вискозиметры делятся на две группы: с неподвижным цилиндром и торсионные вискозиметры.
вискозиметры делятся на две группы: с неподвижным цилиндром и торсионные вискозиметры. ;
; .
. полушарий достаточно разработана [51, 54]. Унгер [50] построил ротационный вискозиметр, в котором цилиндры были заменены вставленными одно в другое полушариями разного радиуса. Муней и Юарт [49] придали дну цилиндров своего прибора коническую форму. Зазор между конусами они выбрали таким, чтобы для каждой точки его отношение к расстоянию от оси вращения было постоянным. Такие вискозиметры называют коницилиндрическими.
полушарий достаточно разработана [51, 54]. Унгер [50] построил ротационный вискозиметр, в котором цилиндры были заменены вставленными одно в другое полушариями разного радиуса. Муней и Юарт [49] придали дну цилиндров своего прибора коническую форму. Зазор между конусами они выбрали таким, чтобы для каждой точки его отношение к расстоянию от оси вращения было постоянным. Такие вискозиметры называют коницилиндрическими. пуаз. Одновременно прибор служит для определения предельного напряжения сдвига в интервале от 50 до 10
пуаз. Одновременно прибор служит для определения предельного напряжения сдвига в интервале от 50 до 10 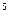 дн/см²
дн/см²  . Вискозиметр РВ-7 применяется как первичный и как вторичный вискозиметр.
. Вискозиметр РВ-7 применяется как первичный и как вторичный вискозиметр.

 а — общий вид; б — схема; 1 — внутренний цилиндр; 2 — внешний цилиндр; 3 — термоизоляционнаяя муфта; 4 — ось вращающейся системы; 5 — шариковые подшипники; 6 — шкив; 7 — блочок; 8 — тормоз; 9 — стрелка; 70 — разделенный круг; 11 — муфта; 12 — штифты; 13 — основная плита прибора; 14 — термопары; 15 — термостат; 16 — термоизоляция; 17 — сосуд для наливания термоста-тирующей жидкости; 18 — мешалка; 19 — отражатель; 20 — муфта; 21 — стопорный винт; 22 — стойка; 23 — крюк; 24 - трос; 25 — влок; 26 — подставка; 27 — установочный винт.
а — общий вид; б — схема; 1 — внутренний цилиндр; 2 — внешний цилиндр; 3 — термоизоляционнаяя муфта; 4 — ось вращающейся системы; 5 — шариковые подшипники; 6 — шкив; 7 — блочок; 8 — тормоз; 9 — стрелка; 70 — разделенный круг; 11 — муфта; 12 — штифты; 13 — основная плита прибора; 14 — термопары; 15 — термостат; 16 — термоизоляция; 17 — сосуд для наливания термоста-тирующей жидкости; 18 — мешалка; 19 — отражатель; 20 — муфта; 21 — стопорный винт; 22 — стойка; 23 — крюк; 24 - трос; 25 — влок; 26 — подставка; 27 — установочный винт. ,
, ,
,
