 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Графическое представление вариационного ряда (гистограмма, полигон, кумулята). Построение графиков по исходным данным.
Полигон распределения строится для рядов, построенных по дискретному признаку. В качестве значений признака при построении берется середина каждого интервала. Открытые интервалы принимаются равными прочим интервалам. Гистограма – столбиковая диаграмма. Основания столбиков – величина интервалов, их высота – частота признака. Графики рядов распределения могут строиться с использованием частот или частостей. Частость — отношение частоты к общему количеству исследуемых элементовКумулята строится с использованием накопленных частот или частостей. По кумуляте можно определить значение показателей структуры.
18. Ассиметрия распределения.К показателям формы распределения относятся показатель ассиметрии и показатель эксцесса. Коэффициент ассиметрии:  Этот прием называется нормированием. На основе этого показателя легко определяется вид ассиметрии. сли числитель положителен, то это положительная правосторонняя ассиметрия. И наоборот. Показатель ассиметрии Пирсона в большей степени оценивает ассиметрию в центра распределения. Чтобы узнать ассиметрию на концах распределения, используется показатель асимерии, рассчитанный на основе центраьного момента третьего порядка.Момент распределения порядка k – среднее арифметическое отклонение к-ой степени индивидуальных значений от некоторой величины А. Этот прием называется нормированием. На основе этого показателя легко определяется вид ассиметрии. сли числитель положителен, то это положительная правосторонняя ассиметрия. И наоборот. Показатель ассиметрии Пирсона в большей степени оценивает ассиметрию в центра распределения. Чтобы узнать ассиметрию на концах распределения, используется показатель асимерии, рассчитанный на основе центраьного момента третьего порядка.Момент распределения порядка k – среднее арифметическое отклонение к-ой степени индивидуальных значений от некоторой величины А.  k – порядок момента, опредеояется степенью.А=0 – начальный моментА= k – порядок момента, опредеояется степенью.А=0 – начальный моментА= 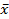 – центральный моментА не равно ни тому, ни другому – условный момент. – центральный моментА не равно ни тому, ни другому – условный момент. Величина коэфициента ассиметрии не имеет предела. Чтобы оценить статистическую значимость, то еть понять под влиянием каких факторов сформировано значение показателя, рассчитывают стандартизованный коэффициент ассиметрии:  , , ( в знаменателе стандартная ошибка коэффициента ассиметрии).Коэффициент ассиметрии берется по модулю, так как может быть и положительным, и отрицательным. Если коэффициент больше или равен 3, то ассиметрия признается существенной, то еть сформированной под влиянием неслучайных факторов. Если меньше 3, то ассиметрия сформирована под влиянием случайных факторов. 19. Эксцесс распределения (куртозис).Характеризует выпад вершины эмпирического распределения вверх или вниз, относительно кривой нормального распределения. Коэф-т эксцесса может быть положительным, что означает выпад ершины вверх, и отрицательным – вниз.  Для оценки существенности эксцесса рассчитывается так же стандартизованный эксцесс (куртозис): Для оценки существенности эксцесса рассчитывается так же стандартизованный эксцесс (куртозис):  Если tex больше или равен 3, то эксцесс признается существенным, то есть сформированным под влиянием неслучайных факторов. Если tex больше или равен 3, то эксцесс признается существенным, то есть сформированным под влиянием неслучайных факторов.
20. Сглаживание эмпирического распределения нормальным законом распределения.В анализе распределения большое значение имеет, насколько эмпирическое распределение признака соответствует нормальному. Для этого частоты фактического распределения нужно сравнить с теоретическими, которые характерны для нормального распределения. по фактическим данным вычислить теоретические частоты кривой нормального распределения, являющиеся функцией нормированных отклонений Порядок расчета теоретических частот кривой нормального распределения: 1) по эмпирическим данным рассчитывают среднюю арифметическую ряда  и среднее квадратическое отклонение s; 2)находят нормированное отклонение t каждой варианты от средней арифметической; 3) по таблице распределения функции и среднее квадратическое отклонение s; 2)находят нормированное отклонение t каждой варианты от средней арифметической; 3) по таблице распределения функции  определяют ее значения; 4)вычисляют теоретические частоты по формуле: определяют ее значения; 4)вычисляют теоретические частоты по формуле:  ,
где N – объем совокупности,
і – длина интервала;5)строят и сравнивают графики эмпирические и теоретических частот. Сумма теоретических и эмпирических частот должна быть равной, но может не совпадать из-за округлений в расчетах. ,
где N – объем совокупности,
і – длина интервала;5)строят и сравнивают графики эмпирические и теоретических частот. Сумма теоретических и эмпирических частот должна быть равной, но может не совпадать из-за округлений в расчетах. 21. Понятие статистической гипотезы и статистического критерия, как инструмента проверки статистических гипотез. Статистическая гипотеза - всякое высказывание о генеральной совокупности, проверяемое по выборке. Статистический критерий — строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза с известным уровнем значимости. Построение критерия представляет собой выбор подходящей функции от результатов наблюдений (ряда эмпирически полученных значений признака), которая служит для выявления меры расхождения между эмпирическими значениями и гипотетическими.
22. Проверка гипотезы о законе распределения.Для проверки гипотезы о соответствии эмпирического распределения закону нормального распределения необходимо частоты фактического распределения сравнить с частотами нормального распределения.  Методика построения теоретического ряда:1)по фактическому интервальному ряду вычисляются значения для каждой группы хозяйств по формуле (для интервальных рядов) для начала и конца интервала. Методика построения теоретического ряда:1)по фактическому интервальному ряду вычисляются значения для каждой группы хозяйств по формуле (для интервальных рядов) для начала и конца интервала.  2) вычисляется вероятность попадания единицы наблюдения в данный интервал при выполнении гипотезы о нормальном законе:  3) определяется теоретическая частота в данной группе, равная совокупности на вероятность попадания в данный интервал. 3) определяется теоретическая частота в данной группе, равная совокупности на вероятность попадания в данный интервал.
 4) находится значене критерия хи квадрат по формуле 4) находится значене критерия хи квадрат по формуле  Если фактическое значение хи квадрат превышает табличное при том же числе степеней свободы, то вероятность соответствия распределения нормальному закону меньше указанной. Если фактическое значение хи квадрат превышает табличное при том же числе степеней свободы, то вероятность соответствия распределения нормальному закону меньше указанной.
23. Ошибки II рода при проверке статистических гипотез.Проверка статистической гипотезы означает проверку согласования исходных выборочных данных с выдвинутой основной гипотезой. При этом возможно возникновение двух ситуаций – основная гипотеза может подтвердиться, а может и опровергнуться. Следовательно, при проверке статистических гипотез существует вероятность допустить ошибку, приняв или опровергнув верную гипотезу.При проверке статистических гипотез можно допустить ошибки первого или второго рода. Ошибкой второго рода называется ошибка, состоящая в принятии ложной гипотезы. Вероятность совершения ошибки второго рода, т. е. принятия ложной гипотезы, обозначается β.
24. Критерий согласия Хи-квадрат (вычисление, использование).Критерий Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитываемыми по формулам нормального распределения.Гипотеза Н0:  — плотность распределения — плотность распределения  генеральной совокупности, из которой взята выборка, соответствует теоретической модели генеральной совокупности, из которой взята выборка, соответствует теоретической модели  нормального распределения.Альтернатива Н1: нормального распределения.Альтернатива Н1:  .Уровень значимости: a.Порядок, применения:1. Формулируется гипотеза, выбирается уровень значимости a.2. Получается выборка объема n .Уровень значимости: a.Порядок, применения:1. Формулируется гипотеза, выбирается уровень значимости a.2. Получается выборка объема n  40 независимых наблюдений и представляется эмпирическое распределение в виде интервального вариационного ряда.3. Рассчитываются выборочные характеристики 40 независимых наблюдений и представляется эмпирическое распределение в виде интервального вариационного ряда.3. Рассчитываются выборочные характеристики  и S. Их используют в качестве генеральных параметров и S. Их используют в качестве генеральных параметров  и и  нормального распределения, с которым предстоит сравнить эмпирическое распределение.4. Вычисляются значения теоретических частот нормального распределения, с которым предстоит сравнить эмпирическое распределение.4. Вычисляются значения теоретических частот  попадания в i-й интервал группировки. Для этого необходимо вычислить: попадания в i-й интервал группировки. Для этого необходимо вычислить: 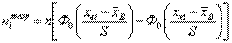
где Ф0(u) — функции Лапласа, xвi и хнi — верхняя и нижняя границы i-го интервала группировки. Если окажется, что вычисленные ожидаемые частоты  некоторых интервалов группировки меньше 5, то соседние интервалы объединяются так, чтобы сумма их ожидаемых частот была больше или равна 5. 5. Значение некоторых интервалов группировки меньше 5, то соседние интервалы объединяются так, чтобы сумма их ожидаемых частот была больше или равна 5. 5. Значение  -критерия рассчитывается по формуле: -критерия рассчитывается по формуле: 
где ni — эмпирические частоты;  – ожидаемые (теоретические) частоты; k — число интервалов группировки после объединения. – ожидаемые (теоретические) частоты; k — число интервалов группировки после объединения. 6. Из таблиц распределения  находится критическое значение находится критическое значение  критерия для уровня значимости а и числа степеней свободы n=n–3. критерия для уровня значимости а и числа степеней свободы n=n–3. 7. Вывод: если  то эмпирическое распределение не соответствует нормальному распределению на уровне значимости. то эмпирическое распределение не соответствует нормальному распределению на уровне значимости. 25. Выборочный метод.
Выборочное наблюдение – один из видов несплошного наблюдения. Приемущество выборочного наблюдения в экономии времени, трудовых ресурсов и возможности расширения программы наблюдения. Генеральная совокупность – совокупность, из которой осуществляется отбор единиц в выборочную совокупность. Выборочная совокупность – совокупность отобранных единиц, по которым в процессе наблюдения будут регистрироваться признаки или значения признаков. N – объем енеральной совокупности, n – объем выборочной совокупности. Задача организации выборочного наблюдения – формирование репрезентативной выборки.
26. Виды выборочного статистического наблюдения.1) собственно-случайная выборка. Без предварительной подготовки генеральной совокупности случайно или механически из нее извлекают единицы в выборочную совокупность. Единица отбора совпадает с единицей наблюдения.2) стратифицированная типологическая (районированная) выборка. В ген совокупности выделяются типы или страты, а затем из каждого типа извлекается число единиц, пропорционально доли каждого типа в общем объеме ген совокупности. Единица отбора совпадает с единицей наблюдения.3) Серийная выборка (гнездовая). В ген совокупности выбираются серии (гнезда) и в выборку случайно или механически производят отбор серий. Внутри серий, 4)опавших в выборку , проводится сплошное наблюдение.4) Многоступенчатая выборка. Связана со сложностью соц-эк явлений, что не поволяет на первом этапе сформировать окончательно выборочную совокупность. На каждом этапе меняется единица отбора.5) многофазная выборка. Каждая фаза отличается объемом программы наблюдения. Чем меньше объем выборки, тем шире программа наблюдения.
27. Способы обеспечения случайности отбора при формировании выборки.1) Случайный отбор. Реализуется с использованием жеребьевки или таблиц случайных чисел.2) Механический отбор. Частный случай лучайного отбора. Реализуется через расчет шага отбора:N/n , где N – ген овокупность, n – объем выборки.
28. Повторная и бесповторная выборки.Повторный отбор – единица ген совокупности, изъятая в выборку, возвращается назад в ген совокупность, и может быть повторно выбрана в выборочную совокупность.Бесповторный отбор – отобранная из ген совокупности единица не возвращается назад. При повторном отборе на протяжении всего отбора сохраняется неизменная вероятность попадания единицы в выборку: p = 1/N При бесповторном отборе вероятность изменяется от 1/N для первой единицы до  для последней единицы отбора. для последней единицы отбора.
29. Расслоенная выборка. Способы формирования выборки при расслоенном отборе.Выборка стратифицированная (расслоенная) – метод извлечения выборки, основанный на предварительном расслоении ген совокупноти на крупные группы. На разных слоях отбор проводится независимо, могут применяться разные способы отбора. Общий объем выборки распределяется между слоями пропорционально их численности. Рекомендуется применять если: 1) каждый слой внутренне однороден, 2) желательно получить репрезентативные данные не только о ген зависимости в целом, но и о ее структурных частях, 3) продиктовано организационными соображениями, 4) трудно получить основу выборки для ген совокупности, но можно для каждого ее слоя, 5) пробемы, связанные с отбором в различных частях ген совокупности сильно различаются.
30. Средняя ошибка выборки.Средняя ошибка выборки прямопропорциональна среднему квадратичному отклонению и обратно пропорциональна квадратному корню из численности выборки. Если выборка используется для определения доли признака, то средняя ошибка выборки определяется: 
31. Предельная ошибка выборки.Расчет объема выборки оуществляется исходя из формулы ошибки выборки. Предельная ошибка выборки:  Величина ошибки выборки обусловлена задачами исследования и задается на стадии проектирования. Значение т зависит от установленного уровня вероятности. Значение дисперсии берется по результатампредшествующих аналогичных исследований. Ошибка выборки берется как абсолютная величина, однако, на практике, размер ошибки задается, как правило, как отностельная величина. Величина ошибки выборки обусловлена задачами исследования и задается на стадии проектирования. Значение т зависит от установленного уровня вероятности. Значение дисперсии берется по результатампредшествующих аналогичных исследований. Ошибка выборки берется как абсолютная величина, однако, на практике, размер ошибки задается, как правило, как отностельная величина.  32. Доверительный интервал для генеральной средней.  33. Определение необходимого объема выборки. 
|




 Этот прием называется нормированием. На основе этого показателя легко определяется вид ассиметрии. сли числитель положителен, то это положительная правосторонняя ассиметрия. И наоборот. Показатель ассиметрии Пирсона в большей степени оценивает ассиметрию в центра распределения. Чтобы узнать ассиметрию на концах распределения, используется показатель асимерии, рассчитанный на основе центраьного момента третьего порядка.Момент распределения порядка k – среднее арифметическое отклонение к-ой степени индивидуальных значений от некоторой величины А.
Этот прием называется нормированием. На основе этого показателя легко определяется вид ассиметрии. сли числитель положителен, то это положительная правосторонняя ассиметрия. И наоборот. Показатель ассиметрии Пирсона в большей степени оценивает ассиметрию в центра распределения. Чтобы узнать ассиметрию на концах распределения, используется показатель асимерии, рассчитанный на основе центраьного момента третьего порядка.Момент распределения порядка k – среднее арифметическое отклонение к-ой степени индивидуальных значений от некоторой величины А.  k – порядок момента, опредеояется степенью.А=0 – начальный моментА=
k – порядок момента, опредеояется степенью.А=0 – начальный моментА= 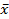 – центральный моментА не равно ни тому, ни другому – условный момент.
– центральный моментА не равно ни тому, ни другому – условный момент. ,
, Для оценки существенности эксцесса рассчитывается так же стандартизованный эксцесс (куртозис):
Для оценки существенности эксцесса рассчитывается так же стандартизованный эксцесс (куртозис):  Если tex больше или равен 3, то эксцесс признается существенным, то есть сформированным под влиянием неслучайных факторов.
Если tex больше или равен 3, то эксцесс признается существенным, то есть сформированным под влиянием неслучайных факторов. и среднее квадратическое отклонение s; 2)находят нормированное отклонение t каждой варианты от средней арифметической; 3) по таблице распределения функции
и среднее квадратическое отклонение s; 2)находят нормированное отклонение t каждой варианты от средней арифметической; 3) по таблице распределения функции  определяют ее значения; 4)вычисляют теоретические частоты по формуле:
определяют ее значения; 4)вычисляют теоретические частоты по формуле:  ,
где N – объем совокупности,
і – длина интервала;5)строят и сравнивают графики эмпирические и теоретических частот. Сумма теоретических и эмпирических частот должна быть равной, но может не совпадать из-за округлений в расчетах.
,
где N – объем совокупности,
і – длина интервала;5)строят и сравнивают графики эмпирические и теоретических частот. Сумма теоретических и эмпирических частот должна быть равной, но может не совпадать из-за округлений в расчетах. Методика построения теоретического ряда:1)по фактическому интервальному ряду вычисляются значения для каждой группы хозяйств по формуле (для интервальных рядов) для начала и конца интервала.
Методика построения теоретического ряда:1)по фактическому интервальному ряду вычисляются значения для каждой группы хозяйств по формуле (для интервальных рядов) для начала и конца интервала. 
 3) определяется теоретическая частота в данной группе, равная совокупности на вероятность попадания в данный интервал.
3) определяется теоретическая частота в данной группе, равная совокупности на вероятность попадания в данный интервал. 4) находится значене критерия хи квадрат по формуле
4) находится значене критерия хи квадрат по формуле  Если фактическое значение хи квадрат превышает табличное при том же числе степеней свободы, то вероятность соответствия распределения нормальному закону меньше указанной.
Если фактическое значение хи квадрат превышает табличное при том же числе степеней свободы, то вероятность соответствия распределения нормальному закону меньше указанной. — плотность распределения
— плотность распределения  генеральной совокупности, из которой взята выборка, соответствует теоретической модели
генеральной совокупности, из которой взята выборка, соответствует теоретической модели  нормального распределения.Альтернатива Н1:
нормального распределения.Альтернатива Н1:  .Уровень значимости: a.Порядок, применения:1. Формулируется гипотеза, выбирается уровень значимости a.2. Получается выборка объема n
.Уровень значимости: a.Порядок, применения:1. Формулируется гипотеза, выбирается уровень значимости a.2. Получается выборка объема n  40 независимых наблюдений и представляется эмпирическое распределение в виде интервального вариационного ряда.3. Рассчитываются выборочные характеристики
40 независимых наблюдений и представляется эмпирическое распределение в виде интервального вариационного ряда.3. Рассчитываются выборочные характеристики  и S. Их используют в качестве генеральных параметров
и S. Их используют в качестве генеральных параметров  и
и  нормального распределения, с которым предстоит сравнить эмпирическое распределение.4. Вычисляются значения теоретических частот
нормального распределения, с которым предстоит сравнить эмпирическое распределение.4. Вычисляются значения теоретических частот  попадания в i-й интервал группировки. Для этого необходимо вычислить:
попадания в i-й интервал группировки. Для этого необходимо вычислить: 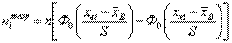
 некоторых интервалов группировки меньше 5, то соседние интервалы объединяются так, чтобы сумма их ожидаемых частот была больше или равна 5. 5. Значение
некоторых интервалов группировки меньше 5, то соседние интервалы объединяются так, чтобы сумма их ожидаемых частот была больше или равна 5. 5. Значение  -критерия рассчитывается по формуле:
-критерия рассчитывается по формуле:
 – ожидаемые (теоретические) частоты; k — число интервалов группировки после объединения.
– ожидаемые (теоретические) частоты; k — число интервалов группировки после объединения. критерия для уровня значимости а и числа степеней свободы n=n–3.
критерия для уровня значимости а и числа степеней свободы n=n–3. то эмпирическое распределение не соответствует нормальному распределению на уровне значимости.
то эмпирическое распределение не соответствует нормальному распределению на уровне значимости. для последней единицы отбора.
для последней единицы отбора.
 Величина ошибки выборки обусловлена задачами исследования и задается на стадии проектирования. Значение т зависит от установленного уровня вероятности. Значение дисперсии берется по результатампредшествующих аналогичных исследований. Ошибка выборки берется как абсолютная величина, однако, на практике, размер ошибки задается, как правило, как отностельная величина.
Величина ошибки выборки обусловлена задачами исследования и задается на стадии проектирования. Значение т зависит от установленного уровня вероятности. Значение дисперсии берется по результатампредшествующих аналогичных исследований. Ошибка выборки берется как абсолютная величина, однако, на практике, размер ошибки задается, как правило, как отностельная величина. 

