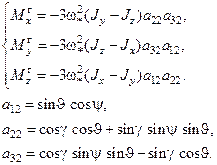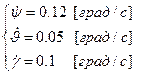ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Случай диагонального тензора инерции
Составление математической модели пространственного движения КА.
Движение летательного аппарата рассматриваются относительно 2 систем координат: орбитальной и связанной. Для перехода от одной СК к другой, целесообразно использовать матрицу направляющих косинусов. Система поворотов систем координат - самолетная, т.е. последовательность поворотов
, где
Коэффициенты матрицы направляющих косинусов будут иметь вид:
Кинематические уравнения движения связанных осей координат относительно опорных можно получить, предварительно спроецировав вектор угловой скорости
Для получения кинематических уравнений движения связанных осей относительно опорной системы координат, необходимо разрешить систему уравнений (1.3) относительно
Для производных углов курса ,тангажа и крена необходимо однозначно определить значения проекции угловой скорости ЛА. Для этого воспользуемся теоремой об изменении кинетического момента:
Вектор кинетического момента в проекциях на оси связанных координат будет иметь вид (по определению):
Тогда в проекциях:
Тогда теорема об изменении кинетического момента в проекциях имеет вид:
Уравнения движения, после раскрытия производных, будут иметь вид:
Случай диагонального тензора инерции
При диагональном тензоре инерции все произведения инерции будут равны нулю:
При рассмотрении будет учитываться влияние гравитационных моментов ЛА, а так же управляющих моментов от маховиков, стабилизирующих полет летательного аппарата. Проекции гравитационного момента относительно связанных осей будут иметь вид:
Тогда для диагонального тензора инерции:
2. Выбор исполнительных органов для обеспечения стабилизации КА:
Необходимо выбрать такие органы управления, чтобы они удовлетворяли следующим требованим по точности: точность по углу: 0,1 ̊; точность по угловой скорости 0,01 ̊/с. В качестве исполнительных органов выбираем двигатели-маховики ДМ14-120 для каналов управления по тангажу и крену с управляющим моментом 0.12 Н/м2 и диапазоном изменения кинетического момента 14 Н*м/c, и двигатель-маховик ДМ5-50для управления по каналу курса с управляющим моментом 0.05 Н/м2 и диапазоном изменения кинетического момента 5 Н*м/c обеспечивающие необходимую точность и скорость стабилизации по углу и угловой скорости.
3. Проведение моделирования режима стабилизации КА в самолетной системе координат.
Зададимся диагональным тенцором инерции и произвольными начальными условиями для значений углов и угловых скоростей по каналам курса, тангажа и крена:
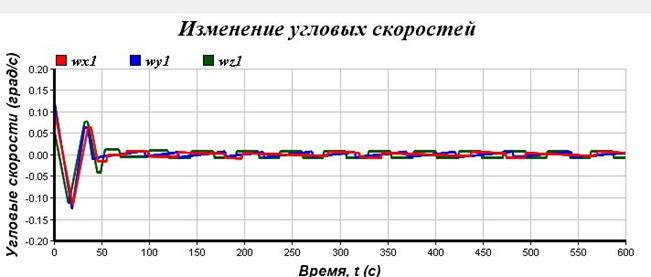
Затем, построим графики изменения углов и угловых скоростей в процессе стабилизации, фазовую траекторию процесса стабилизации.
Вывод: космический аппарат стабилизируется, на фазовом портрете можно наблюдать, что система, войдя в предельный цикл, соответствует заданным требованиям точности по углам и угловым скоростям. По форме предельного цикла можно сделать вывод, что на систему действует малый возмущающий момент, который объясняется накоплением кинетического момента в двигателях-маховиках (формула 1.5)
4. Рассмотрение влияния перекрестных связей на процесс разворота КА. Для рассмотрения влияния перекрестных связей проведем моделирование стабилизации КА, введя в тензор инерции недиагональные составляющие. Для наглядности зададимся ненулевыми начальными условиями только по каналу крена и проведем моелирвание.
На графиках представлены 2 вида предельных циклов. Первый предельный цикл показывает состояние системы без изменения закона управления после ввода недиагональных элементов тензора инерции. Как видно из этого графика, система больше не удовлетворяет заданным требованиям по точности стабилизации. На втором графике представлено состояние системы с измененным законом управления, которая удовлетворяет требованиям точности. Вывод: при наличии недиагональных компонентов тензора инерции в системе возникают перекрестные связи, негативно влияющие на систему управления, т.к. они усложняют процесс стабилизации. Влияние недиагональных компонентов тензора инерции на стабилизацию системы объясняется формулой 1.6 Также, на фазовом портрете можно наблюдать изменение вида предельного цикла по каналу крена, объясняющееся тем, что кинетические моменты маховиков по другим каналам из-за нулевых начальных условий накапливаются меньше, а следовательно, в меньшей степени влияют на канал крена (1.5)
5.Исследование влияния возмущающих моментов на угловое движение КА.
Для проведения этого исследования произвольно зададимся внешними возмущающими моментами и проведем моделирование стабилизации с теми же начальными условиями, что и в третьем пункте.
Из графиков видно, что наличие внешних возмущающих моментов оказывает сильное влияние на систему: увеличивает время установления предельного цикла; увеличивает необходимые набор кинетических моментов двигателей-маховиков, что в свою очередь негативно сказывается на дальнейшем управлении; изменяет форму предельного цикла. Также, для удовлетворения требованиям по точности стабилизации необходимо изменять закон управления, что приводит к более частым включениям управляющих органов, а следовательно, большим энергозатратам.
Вывод: Результаты моделирования показывают, что наличие недиагональности тензора инерции и возмущающих моментов приводит к ухудшению качества работы системы стабилизации. В случае, рассмотренном выше, введение недиагонального тензора привело к появлению перекрестных связей между каналами, что значительно усложнило выполнение стабилизации системы. Введение возмущающих моментов привело к увеличению времени переходных процессов по всем каналам управления и ухудшение характеристик управления системой.
|




 (1.1)
(1.1) -оси связанной СК,
-оси связанной СК, оси опорной СК.
оси опорной СК. (1.2)
(1.2) на оси связанных координат.
на оси связанных координат. (1.3)
(1.3) .
.
 где
где -кинетический момент
-кинетический момент -сумма внешних моментов, действующих на ЛА.
-сумма внешних моментов, действующих на ЛА. , в проекциях на оси координат:
, в проекциях на оси координат: ;
;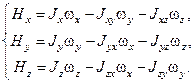 (1.4)
(1.4) (1.5)
(1.5)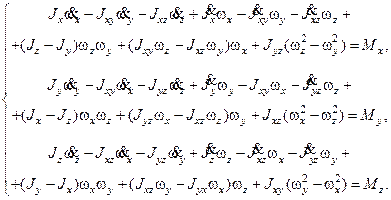 (1.6)
(1.6) , тогда уравнения движения(1.6.) преобразовываются к виду:
, тогда уравнения движения(1.6.) преобразовываются к виду: (1.7)
(1.7) ;
;