ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Элементы векторной алгебры, аналитической геометрии и линейной алгебры. Комплексные числа.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное образовательное учреждение высшего Профессионального образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» (МИИТ)
Составители: Блистанова Л.Д., д.ф.-м.н., проф., Голечков Ю.И., д.ф.-м.н., доц., Захарова М.В., к.ф.-м.н., доц., Сперанский Д.В., д.т.н., проф.
МАТЕМАТИКА Задания на контрольные работы № 1 – 3 для студентов 1 курса заочной формы обучения направлений: 220400.62 – Управление в технических системах, профиль – УТ; 230400.62 – Информационные системы и технологии, профиль – ИС; 230700.62 – Прикладная информатика, профиль – ИИ.
Москва 2011г. Методические указания по выполнению контрольных работ
Задачи, включенные в контрольную работу, взяты из сборника задач, подготовленного коллективом преподавателей кафедры «Высшая и прикладная математика» РОАТ МГУПС. Все задачи имеют тройную нумерацию, которая включает номер раздела из сборника задач, уровень сложности задачи и порядковый номер задачи. Студент выполняет те задачи, последняя цифра номера которых совпадает с последней цифрой его учебного шифра. Например, студент, учебный шифр которого имеет последнюю цифру 1, в контрольной работе №1 решает задачи 1.1.61, 1.2.1, 2.1.31, 3.1.1, 4.2.1; в контрольной работе №2 – 6.2.1, 7.2.1, 7.2.21, 7.2.31, 7.3.11; в контрольной работе №3 – 8.1.21, 8.2.41, 8.3.1, 9.1.41, 9.3.81. Перед выполнением контрольной работы студент должен ознакомиться с содержанием разделов рабочей программы, на освоение которых ориентирована выполняемая контрольная работа. Необходимую учебную литературу студент может найти в рабочей программе (в программе указана как основная, так и дополнительная литература). Каждая контрольная работа выполняется в отдельной тетради, на обложке которой должны быть указаны: дисциплина, номер контрольной работы, шифр студента, курс, фамилия, имя и отчество студента. На обложке вверху справа указывается фамилия и инициалы преподавателя-рецензента. В конце работы студент ставит свою подпись и дату выполнения работы. В каждой задаче надо полностью выписать ее условие. В том случае, когда несколько задач имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера. Решение каждой задачи должно содержать подробные вычисления, пояснения, ответ, а также, в случае необходимости, и рисунки. После каждой задачи следует оставлять место для замечаний преподавателя-рецензента. В случае невыполнения этих требований преподаватель возвращает работу для доработки без ее проверки.
КОНТРОЛЬНАЯ РАБОТА № 1 Элементы векторной алгебры, аналитической геометрии и линейной алгебры. Комплексные числа. 1.1.61–1.1.70.Выполнить действия с векторами. 1.1.61. Даны векторы 1.1.62. Найти 1.1.63. Определить угол между векторами 1.1.64. Показать, что векторы 1.1.65. Найти скалярное произведение векторов 1.1.66. Определить угол между векторами 1.1.67. При каком значении mвекторы 1.1.68. Найти векторное произведение векторов 1.1.69. Вычислить площадь параллелограмма, построенного на векторах 1.1.70. Найти работу силы 1.2.1–1.2.10.Даны векторы
2.1.31. Составить уравнение прямой, проходящего через т. 2.1.32. Составить уравнение прямой, проходящей через т. 2.1.33. Составить уравнение перпендикуляра, проходящего через середину отрезка 2.1.34. Составить уравнение прямой, проходящей через т. 2.1.35. Составить уравнение прямой, проходящей через т. 2.1.36. Составить уравнение перпендикуляра, проходящего через середину отрезка 2.1.37. Составить уравнение прямой, проходящей через т. 2.1.38. Составить уравнение прямой, проходящей через т. 2.1.39. Составить уравнение перпендикуляра, проходящего через середину отрезка 2.1.40. Составить уравнение прямой, проходящей через т. 3.1.1–3.1.10.Дана матрица А. Найти матрицу А-1, обратную данной, методом Жордана–Гаусса. Сделать проверку, вычислив произведение А.А-1.
4.2.1–4.2.10.Даны два комплексных числа. Необходимо: а) выполнить действия в алгебраической форме; б) найти тригонометрическую форму числа z, найти z20 . 4.2.1. a) 4.2.2. a) 4.2.3. a) 4.2.4. a) 4.2.5. a) 4.2.6. a) 4.2.7. a) 4.2.8. a) 4.2.9. a) 4.2.10. a) КОНТРОЛЬНАЯ РАБОТА № 2 |



 и
и  . При каком значении m эти векторы перпендикулярны?
. При каком значении m эти векторы перпендикулярны? , если a =2, b = 3,
, если a =2, b = 3, 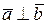 .
. и
и  .
. ,
,  ,
,  компланарны.
компланарны.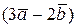 и
и  , если a = 4, b = 6 и угол между векторами
, если a = 4, b = 6 и угол между векторами  и
и  равен p / 3.
равен p / 3. и
и  .
. и
и  перпендикулярны?
перпендикулярны?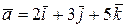 и
и  .
. и
и  .
. на перемещении
на перемещении  ,если F = 2, s = 5 и угол между векторами
,если F = 2, s = 5 и угол между векторами 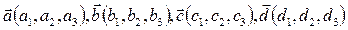 в базисе (
в базисе (  ). Показать, что векторы
). Показать, что векторы  образуют базис. Сделать чертеж.
образуют базис. Сделать чертеж.









 перпендикулярно прямой. Сделать чертеж.
перпендикулярно прямой. Сделать чертеж. перпендикулярно прямой
перпендикулярно прямой  . Сделать чертеж.
. Сделать чертеж. , если
, если  ;
;  . Сделать чертеж.
. Сделать чертеж. и перпендикулярной прямой
и перпендикулярной прямой 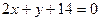 . Сделать чертеж.
. Сделать чертеж. и параллельной прямой
и параллельной прямой  . Сделать чертеж.
. Сделать чертеж. ;
;  . Сделать чертеж.
. Сделать чертеж. и перпендикулярной к прямой
и перпендикулярной к прямой  . Сделать чертеж.
. Сделать чертеж.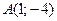 и перпендикулярной прямой
и перпендикулярной прямой 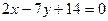 . Сделать чертеж.
. Сделать чертеж. ;
;  . Сделать чертеж.
. Сделать чертеж. и параллельной прямой
и параллельной прямой  . Сделать чертеж.
. Сделать чертеж.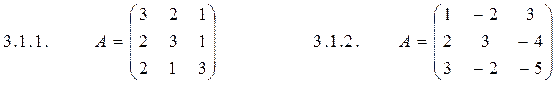




 , б) z =
, б) z =  .
. , б) z =
, б) z =  .
. , б) z =
, б) z =  .
. , б) z =
, б) z =  .
. , б) z =
, б) z =  .
. , б) z =
, б) z =  .
. , б) z =
, б) z =  .
. , б) z =
, б) z =  .
. , б) z =
, б) z =  .
. , б) z =
, б) z =