 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| б)Денелерді шарнирлермен байланыстыру.
1)Жылжымалы шарнир(каток).Жылжымалы шарнир дененің тіреу жазықтығымен қозғалыс жасауына кедергі келтірмейді де оған перпендикуляр бағыттағы қозғалысын шектейді.Сол себепті оның реакциясы әр уақытта тіреу жазықтығына перпендикуляр бағытталады.(1,13 а, б, в суреттер). 2)Жылжымайтын цилиндрлік шарнир.Цилиндрлік шарнирдің өсі бойымен дене сырғып қозғала алады.Сондықтан да цилиндрлік шарнир реакциясы шарнир өсіне перпендикуляр жазықтықта жатады.(1,14 а, б суреттер). 3)Жылжымайтын сфералық шарнир.Сфералық шарнир дененің бір нүктесін қозғалмайтын етіп бекітеді.Дене осы бекітілген нүктесі арқылы өтетін осьтен айнала алады.Қозғалмайтын нүутедегі реакция кеңістікте кез келген бағытта болуы мүмкін.Бағыты да, шамасы да белгісіз, толық R(үстінде сызығы бар) реакциясының орнына әдетте оның координаталық осьтердегі проекциялары ізделінеді(1,15 а, б суреттер). в)Иілгіш байланыстар және стерженьдік байланыстар 1) Жіп(қанат, шынжыр).Созылмайтын, иілгіш жіп түрінде берілген байланыс дененің бі+р ғана бағыттағы қозғалысын шектейді, яғни иілгіш байланыстар тек қана созылатын болады.Сондықтан да жіп реакциясы әр уақытта жіптің бойымен ол ілінген нүктеге қарай бағытталады.(1,16 а, б суреттер) 2) Стерженьдік байланыстар.Стерженьдің байланыстар салмақсыз, ұштары шарнирлермен бекітілген стерженьдер арқылы беріледі.Иілгіш байланыстарға қарағанда стерженьдер дененің екі бағыттағы қозғалысына(стержень бойымен) кедергі жасайды.Стерженьдер берілген күштер әсерлерінен созылуға не сығылуға қарсы жұмыс үстейді.Стерженьдік байланыстар реакциясы стерженьдер осьтерінің бойымен немесе стержень ұштарындағы шарнирлерді қосатын сызықтың бойымен бағытталады.(1,17 а, б суреттер) г. Қозғалмастай етіп қадалған денелер. Кейбір жағдайларда балканы бір ұшы қабырғаға(1,18 а сурет) немесе еденге(1,18 б сурет) қазықша қадай бекітіледі. Бұл бекітуді – қадалған ұш(заделка) деп атаймыз. Қозғалмайтын шарнирге қарағанда байланыстың мұндай түрі денеге тағы да бір кедергі жасайды.Ол берілген дененің байланысқа қарағандағы айналысын болдырмайды.Сондықтан да R(үстінде сызығы бар) реакциямен бірге реакциялық момент те МR(үстінде сызығы бар) әсер етеді.Сөйтіп қадалған ұштың берілген А денеге жасайтын әсері екі элементтен R(үстінде сызығы бар) күш пен МR(үстінде сызығы бар) моменттен тұрады.Мұндағы R(үстінде сызығы бар) реакциясының бағыты алдын ала белгісіз.Ол әрбір дербес жағдайда берліген күштерге және қарастырылатын дененің орналасуына байланысты анықталады.
17-сұрақ. Күштің нүктеге қатысты моменттерінің скалярлық және векторлық анықтамаларын беріңіз. 1. Күштің моментінің скалярлық анықтамасы. Күштің нүктеге қатысты моменті деп «+», не «-» таңбасымен алынған күш пен оның сол нүктеге қатысты иінінің көбейтіндісіне тең болатын шаманы айтамыз. 0 нүктесінен күштің әсер ету сызығына дейінгі қашықтықты күштің осы 0 нүктесіне қатысты иіні деп атаймыз.
2. Күштің нүктеге қатысты моментінің векторлық анықтамасы. 3. Күшінің өске қатысты моменті. Күштің өске қатысты моменті деп күштің берілген өске перпендикуляр жазықтықтағы проекциясының өс пен жазықтықтың қиылысу нүктесіне қатысты алынған моментінің «+» немесе «-» таңбасымен алынған сан шамасын айтамыз. Абсолют қатты денеге әсер етуші шамалары тең, өзара параллель және қарама-қарсы бағытталған екі күштің жүйесін қос күш деп атаймыз. Күштердің әсер ету сызықтарының ең жақын ара қашықтығын, қос күштің иіні деп атаймыз. Қос күш әсері қос күш моментімен анықталады. Қос күш моменті деп модулі, оның күші мен иінінің көбейтіндісіне (Ғ, h) тең, ал бағыты қос күш жазықтығына перпендикуляр болып келетін векторды айтамыз.
18-сұрақ. Күштің өске қатысты моменттері. Күштің нүктеге және өске қатысты моменттерін координаттық әдіспен есептеу. Күштің өске қатысты моменті. Күнделікті тәжірибеден күштің денелерді өсті айналдыра қозғалатынын білеміз. Күштің денені өстен айналдырушы әсерін сипаттаушы шама-өске қатысты күш моменті. Енді соған екі түрлі анықтама береиік. Бірінші анықтама: Күштің өске қатысты моменті деп берілген өске перпендикуляр жазықтықтағы проекциясының өс пен жазықтықтың қиылсу нүктесіне алынған моментінің «+» , немесе «-» таңбасымен алынған сан шамасын айтамыз. Бізге А нүктесіне түсірілген Жоғалыдағы анықтаманы былай түсіндіруге болады:
(1) Теңдігі күштің OL өсіне қатысты моментін табу, Р―ж күштің проекциясының С нүктесіне қатысты моментін есептеуге келтірілетін көрсетеді.
Мұндағы h-күш проекциясы Рж-ның С нүктесіне қатысты алынған иіні, яғни h=CD (ж-жазықтығында С нүктесінен А1В1 кесіндісіне жүргізілген перпендикуляр )(1 сурет)
(1) және (2) салыстырудан күштің өске қатысты моментінің неге тең болатынын анықтайтын формула шығады
(3) формуладағы «+»немесе «-» таңбасын алатынымызды анықтауда оң бұранда ережесіне сүйенеміз. Егер L өсінің оң ұшынан қарағанда Екінші анықтама:Кейде есептеп шығару кезінде өске қатысты күш моментін оның екінші бір анықтамасы арқылы есептеу қолайлы. Ол былай айтылады: Күштің өске қатысты моменті деп өстің кез келген бір нүктесіне қатысты алынған күш моменті векторының осы өстегі проекциясын айтады: Бізге А нүктесіге түсірілген Осы өстің кезкелген бір нүктесі С-ға қатысты
Түрінде жаза аламыз немесе (4)формуланы ескеріп (5) қатысты мынадай басқа түрге келтіругеболады
(6) өрнегі Өстік моменттің екі анықтамасы (3) және (6) бір біріне тең. Бұл дәлелдеу үшін ΔАВС мен ΔА1В1С1 аудандарының арасындағы тәуелділікті қарастырайық.(2сурет). SΔABC=SΔABC Өстік моменттің (7)-формуламен өрнектелетін бірінші анықтамасы: 2SΔABC=ml( Болатынын көрсетеді. Ал (2) бойынша 2SΔABC=mc( (8)және (9)теңдіктерін ескеріп (7) былай жазамыз Pж h=mс (9)теңдіктің оң жағы күш моменті векторының ОІ өсіне түсірілген проекциясына тең екенін ескерсек мынаны аламыз: Pжh=npl( Бұл өстік моменттің екі анықтамасының бір біріне теңбе тең екендігін корсетеді: Күштің нүктеге және өске қатысты моменттерін координаттық әдіспен есептеу. Р күшінің О нүктесіне қатысты моментін есептеу керек болсын. Бас нүктесі О нүктесінде болатын Охуz жүйесін алайық (3сурет) Күштің О нүктесіне қатысты вектор моментін мына түрдегі анықтауыш арқылы жаза аламыз: Мұндағы Анықтаушы оның бірінші жолының элементтері Сонда мынау шығады: Бұл теңдік
Формулаларымен анықталады. Өстік моменттерді аналитикалық әдіспен есептеу осы формулалар арқылы жүргізіледі. Ол үшін
Нүктеге қатысты момент векторының бағыттаушы косинустары:
Мұндағы α,β,γ момент векторының Ox, Oy,Oz өстерімен жасайтын бұрыштары.
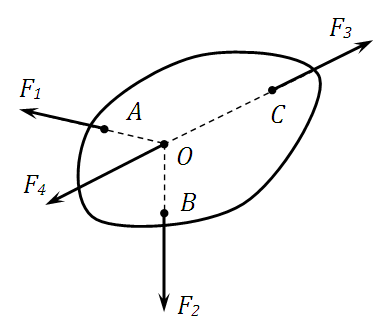
19-сұрақ. Бір нүктеге түсірілген күштер жүйесі және олардың тең әсер етушісін анықтау тәсілдері. Берілген қатты дененің А нүктесінде Р1 және Р2 күштері әсер етеді дейік.күштер араындағы күш 𝛼-ға тең болсын. Күштер параллелограмы туралы аксиоманы қолданақ: (Р1,Р2)~R , R =Р1+Р2 Демек, бір нүктеге түсірілген екі күштен тұратын жүйе бір R теңәсерлі күшке теңестіріледі. Бұл күштер Р1,Р2 күштерінің геометриялық күштеріне тең. Теңәсерлі R күшінің модулін анықтау мақсатымен теңдігінің екі жағында квадрат дәрежеге шығарып ,одан түбір табу керек: R R күшінің бағытын табу үшін, бұл теңәсерлі күшпен Р1,Р2 күштер арасындағы 𝛼,𝛽 бұрыштарын анықтау керек.(1-сурет)
Синустар теоремасын қолданып үшбұрыштың АВС дан мынадай теңдікті аламыз:
Р1,Р2 және 𝛼 берілген жағдайда (2) формула арқылы тең әерлі күш R-дің модулін табамыз. Содан соң 3-ші формуладан Теңәсерлі күш толық параллелограмды құрмай-ақ ,оның жартысына тең АВС үшбұрышын құру арқылыда табуға болады. Мысалы Р1 күшіне паралель және оған тең вектор жүргіземіз. Осылайша қоылған сынық сызықтың бастапқы нүктесі мен ақырғы нүктесінін қоатын вектор, іздеп отырған , екі күштің тең әсерлі күші , R-ді белгілейді. 2-сурет. АС= R векторы күштер үшбұрышы АВС-ның тұйықтаушы қабырғасы деп аталады. Бір нүктеге түсірілген үш күштің тең әсерлі күші. Қатты дененің бір нүктесі А-ға , бір жазықтықта жатпайтын Р1,Р2,Р3 үш күш түсірілген дейік. Жазықтақта жатпайтын бұл үш күштен тұратын жүйе тең әсерлі R күшке келтіріледі. Теңәсерлі күштің шамасы мен бағытын анықтау үшін біртіндеп күштер үшбұрыштың құру әдістерін қолданамыз. Р1күшінің соңғы нүктесі В-дан бастап Р2 векторын жүргізнміз. Р2, -векторының шамасы Р2-ның шамасына тең және оған параллель бағыттылған. Оның соңғы нүктесі С, нүктесінен бастап. Р3, векторын жүргіземіз. Бұл вектор А нүктесіндегі Р3 векторына тең.Соңғы вектордың сонғы нүктесін Е, деп белгілейміз. Енді А нүктесін Е, нүктесімен қосу арқылы R, векторын табамыз. АЕ, =R, векторы АВ С, Е, сынық сызығының тұйықтаушы қабырғасына тең. Сөйтіп, бұл айтылғандардан мынадай қорытынды келтіреміз. Бір жазықтықта жатпайтын ,бір нүктеге түсірілген Р1,Р2,Р3 күштерінің векторлық қосындысы , осы күштер арқылы құрылған , параллелепипедтің диагоналімен бейнеледі. (Р1,Р2,Р3)~ R , R= Р1+Р2+Р3 Күштердің берудің және қосудың аналитикалық әдісі. Күшті және күштер жүйесінің тең әсерлі күшін табуда, ең жие қолданылатын әдіс. Мұнда ең алдымен өз қалауымызша қандайда тікбұрышты декараттық координаттар жүйесін Охуz-ті сайлап аламыз. Күштің координаттар өстеріндегі проекциялары және оның бастапқы нүктесінің координаттары белгілі болсын: Рх,Ру,Рz, (немесе Х,У,Z) және x,y,z. Берілген осы шамалары арқылы Р күштің сан шамасын (модулін) және оның бағытын анықтау керек. Күш бағыты оның бағыттаушы косинустары: cos𝛼 cos𝛽 cos𝛾 арқылы анықталады. Күштің тікбұрышты координаттық өстердегі проекциялары арқылы , оның модулін мына теңдікпен анықтаймыз: Ал оның бағыттаушы косинустары мына түрде анықталады:
Сөйтіп куштің координаттар өстеріндегі проекциялары Х,У,Z берілсе, оның модулін осы формула арқылы анықтауға болады. Күштің түсу нүктесі А-ның орны оның берілген координаттары x,y,z арқылы табамыз.
20-сұрақ. Жинақталушы күштер жүйесі. Жинақталушы күштер жүйесінің тепе-теңдік шарты мен теңдеулерін жазыңыз. Теорема.Қатты денеге түсірілген жинақталатын күштер жүйесі тепе-теңдікте болу үшін оның тең әсерлі күшінің нөлге тең болуы қажет және жеткілікті. Күштердің тепе-теңдік шарттарын геометриялық немесе аналитикалық түрде келтіруге болады. 1. Тепе-теңдіктің геометриялық шарты. Күштер жүйесінің Демек, жинақталатын күштер жүйесі тепе-теңдікте болу үшін осы күштерден тұрғызылған күштер көпбұрышының тұйық болуы қажет және жеткілікті. 2. Тепе-теңдіктің аналитикалық шарттары. Жүйенің бас векторының аналитикалық модулі (1.2.3) өрнегімен анықталады:
(1.2.8) теңдеулері тепе-теңдік шарттарының аналитикалық түрін береді:кеңістіктегі жинақталатын күштер жүйесі тепе-теңдікте болу үшін осы күштердің координата өстерінің үшеуінің әрқайсысына проекцияларының қосындысының нөлге тең болуы қажет және жеткілікті. Қатты денеге әсер ететін жазықтықтағы жинақталатын күштер жүйесі тепе-теңдікте болу үшін күштердің координата өстерінің екеуіне проекцияларының қосындысының нөлге тең болуы қажет және жеткілікті:
Абсолют қатты денеге әсер ететін күш жылжымалы вектор болғандықтан, жинақталатын күштер жүйесі бір нүктеге түсірілген күштер жүйесіне пара-пар (1.11 ә) суреттегі О нүктесі). Теорема.Жинақталатын күштер жүйесін осы күштердің геометриялық қосындысына тең және олардың әсер ету сызықтарының қиылысу нүктесіне түсірілген тең әсерлі күшпен алмастыруға болады. Дәлелдеу. Әсер ету сызықтары О нүктесінде қиылысатын Статиканың 1 және 2 аксиомаларының салдарына сүйеніп барлық күштерді олардың әсер ету сызықтарының бойымен О нүктесіне көшіреміз (1.11 ә) сурет). Статиканың 3 аксиомасына сүйеніп Алынған
Осылай барлық күштерді қоссақ, берілген күштер жүйесінің тең әсерлі күші болатын бір
Жинақталатын күштер жүйесінің тең әсерлі күшін күштер көпбұрышын тұрғызу арқылы да анықтауға болады. Түсінікті болу үшін сурет жазықтығында жатқан төрт күш үшін көпбұрыш тұрғызайық (1.12 а) сурет).
Жинақталатын күштер жүйесінің тең әсерлісі болатын
Жинақталатын күштер жүйесінің тең әсерлі күшін аналитикалық түрде анықтауға болады. Ол үшін геометрияның келесі теоремасына сүйенеміз: күштердің векторлық қосындысының қалаған өске проекциясы қосылғыш күштердің осы өске проекцияларының алгебралық қосындысына тең. Осыған сәйкес, жинақталатын күштер жүйесін құратын күштердің декарттық координата өстеріне проекцияларын біле отырып тең әсерлі күштің осы өстерге проекцияларын анықтауға болады:
Сонда тең әсерлі күштің модулі мынандай болады:
Оның бағыты бағыттаушы косинустармен анықталады:
Бір жазықтықта орналасқан күштер үшін:
21-сұрақ. Өзара паралель емес үш күштер туралы теорема және оның мағынасын сипаттаңыз. Егер үш өзара параллель емес күштер тең күштер жүйесiн құрастырса, онда олар бiр жазықтықта жатады және бiр нүктеде қиылысады. Бұл теореманы үш күш туралы теорема деп атаймыз.
Теорема оңай дәлелденедi. Күштер паралелль болмағандықтан олардың ең болмаса екеуi бiр нүктеде қиылысады, ендi екi күштi алдымен осы нүктеге сырғытып, қосайық. Сонда бұл күш алғашқы күштерден қалған күшпен тепе-теңдiкте болуы тиiстi. Басқаша айтқанда олар бiр түзу бойымен қарама-қарсы бағытталады. Сондықтан үш күште бiр нүктеде қиылысады және бiр жазықтықта жатады. Керi оқылған теорема орындалмайды, өйткенi кез келген үш күш тепе-теңдiкте болмауы да ықтимал. Теорема екi күштiң бағыты берiлсе үшiншi күштiң бағытын табуға мүмкiншiлiк бередi.
22-сұрақ. Қос күштер туралы түсінік. Қос күштер моменті. Қос күштер жүйесінің тепе теңдік шарттарын сипаттаңыз. Қос күш. Абсолют қатты денеге әсер етуші шамалары тең,өзара параллель және қарама –қарсы бағытталған екі күштің жүйесін қос күш деп атаймыз. Күштерді
Қос күш (
Бұл теңдіктен ол вектордың модулінің,
Бұл векторлық көбейтіндінің модулі мен бағытын анықтайық.Оның модулін, (1-сурет) көрсетілген қос күштің иіні болып табылатын, h арқылы өрнектейік.Сонда ļ Бұл (3) теңдігін қос күш моменті векторының модулін анықтайтын (1) немесе (2)теңдігімен салыстырып қарасақ, онда екі вектордың модульдерінің тең екендігін көреміз ļ Осындан кейін
Қос күш моментінің қасиеттері.a) Қос күш моменті құраушы күштердің кез келген бір центрге қатысты алынған моменттерінің геометриялық қосындысына тең*2
Қос күшті құраушы . Мұнда біз
(6) теңдігі қос күш моментінің құраушы күштердің кез келген центрге қатысты моменттерінің қосындысына тең екенін дәлелдейді.б)Қос күштің моменті оның бір күшінің әсер ету сызығының кез келген нүктесіне қатысты алынған моментіне тең.Осыны дәлелдеу үшін қос күштің бір күші
B нүктесі
Сонымен (8) (9) теңдіктерін өзара салыстырудан алатынымыз (10)қатынасы қос күш моменті оның бір күшінің екінші күш бойында жатқан кез келген бір нүктеге қатысты алынған моментіне тең екенін көрсетеді.Қос күштер эквивалеттілігі. а) Қос күшті қатаң фигура тәрізді өз жазықтығында бір орыннан екінші орынға параллель тасымалдауғажәне кез келген бұрышқа бұруға болады.Бұдан қос күштің қатты денеге әсері өзгермейді б)Қос күштің жазықтығын параллель көшіруге болады.Бұдан қос күштің қатты денеге әсері өзгермейді. В)Қос күштің иінін және күшің , олардың көбейтіндісі өзгермейтіндей етіп,өзгерген түрде алуға болады.Бұдан қос күштің қатты денеге жасайтын мех-қ әсері өзгермейді. Вариньон теоремасы.Күштердің жазық жүйесі Теорема: Күштердің жазық жүйесінің теңәсерлі күшінің,осы күштер жатқан жазықтыққа алынған,кез келген бір центрге қатысты моменті жүйедегі барлық күштердің сол центрге қатысты моменттрінің қосындысына тең болады. Қатты денеге әсер етіп тұрған ( Теңәсерлі күш
23-сұрақ. Динамиканың мәселелері, негізгі түсініктері мен ұғымдары. Нүкте қозғалысының дифференциал теңдеулерiн сипаттаңыз (барлық түрлері). Динамиканың негізгі заңдары мен мәселелері. Динамика негізінде, аксиомалар ретінде қабылданатын, бірнеше қағидалар жатады. Бұл қағидалар табиғаттағы құбылыстарға жасалған көптеген жылғы бақылаулар мен тәжірибелерді дәне қоғамдық практика нәтижелерін жалпылап қорытындылаудан алынған. Механика аксиомаларын ең толық және ақырғы түрінде айтып берген И.Ньютон еді. Сондықтан да оларды Ньютон заңдары д.а. Ньютонның бірінші заңы(инерция заңы).Егер материялық нүктеге ешбір күш әсер етпесе, онда ол өзінің тыныштық күйін немесе түзу сызықты бірқалыпты қозғалысын сақтайды. Ньютонның бірінші заңы материялық денелердің негізгі бір қасиетін, яғни өзін өзі қозғалысқа келтіре алмайтын қасиетін сипаттайды. Ал екінші жағынан бұл зат денелер өзіне түсірілген сыртқы күштердің әсерінен бірден қозғалысқа келе қоймай өзінің тыныштық күйін немесе түзу сызықты бірқалыпты қозғалысын бірте өзгерте қоймай, ондай күйін сақтап қалуға тырысатын да қасиеті бар екенін көрсетеді. Оны денелердің инерциясы немесе материяның инерттігі дейді. Инерттілік барлық денелерге тән қасиет. Дене жылдамдығын берілген шамаға дейін өзгерту үшін оған түсірілген күш әсері белгілі бір уақытқа созылуы керек. Ол уақыт аралығы неғұрлым көп болса, дене соғұрлым инерттірек келеді. Өзара әсерлесетін екі дененің қайсысы жылдамдығын баяуырақ өзгертсе, сонысы инерттілеу болады. Ньютонның –заңын инерция заңы деп те атайды. Инерция заңында айтылатын материялық нүктенің түзу сызықты бірқалыпты қозғалысын инерциялық қозғалыс дейміз. Инерция заңы және Ньютонның басқа да заңдары қандай да бір қозғалмайтын координаттар өстеріне қатысты айтылады. Ньютон заңдары орындалатын координаттар өстерінің жүйесін негізгі немесе абсолюттік жүйе дейді. Ньютон заңдары, әсіресе инерция заңы орынды болатын координаттар өстерінің жүйелерін иерциялық жүйелер д.а. мұндай жүйелерге қатысты қаралатын денелердің, материялық нүктелердің қозғалыстары абсолют қозғалыстар д.а. Ньютонның 2 заңы( негізгі заң) Материялық нүктеге әсер етуші күш осы нүкте үдеуімен бағытталады және шамасы үдеуге пропорционал болады. Материялық нүктеге түсірілген күшті F деп, нүкте массасын m деп, ал үдеуін а деп белгілейік: F= ma Бұл теңдіктен нүктеге әсер етуші күш нүктенің массасы мен оның үдеуінің көбейтіндісіне тең екенін көреміз. (1)теңдігі динамиканың негізгі заңы д.а. негізгі заң нүктені қозғалысқа келтіретін күшпен нүкте массасы және оның үдеуінің арасындағы тәуелділікті береді. Халықаралық бірліктер жүйесінде негізгі бірліктер былай алынған: ұзындық бірлігі – 1м, уақыт бірлігі – 1с, масса бірлігі – ньютон(Н) д.а. 1Н-ға тең күш 1 кг массаға, 1см/с² тең үдеу береді. CGS жүйесінде бірлік күш үшін 1г массаға 1см/с² үдеу беретін күш алынады. Күштің бұл бірлігін дина д.а. Бірліктердің техникалық жүйесінде негізгі бірліктер қатарына күш бірлігі алынады. Ол да килограмм (кГ) д.а. мұнда масса бірлігі туынды бірлік болады: [m]=[F] * [a]¯¹ 1 кг күшпен 1Н арасындағы тәуелділікті (3) формула арқылы табамыз: 1килограмм күш = g * 1 килограмм масса немесе 1кГ = 9,81 Демек бір килограмм – күш 9,81 Ньютонға тең. Ньютонның 3 заңы ( әсер және қарсы әсер заңы)материялық екі нүкте бір біріне оларды қосатын түзу бойымен қарама қарсы бағытталған, модульдері тең күштермен әсер етеді. Мысалы, үстел үстіндегі дене өзінің салмағынд |










 (6)
(6) күштің 0 нүктесіне қатысты моменті деп радиусвектор
күштің 0 нүктесіне қатысты моменті деп радиусвектор  мен
мен  күші және ОL өсі берілсін. Өстің кез келген бір С нүктесі арқылы оған пнрпендикуляр жазықтық (ж)-ны жүргізейік.
күші және ОL өсі берілсін. Өстің кез келген бір С нүктесі арқылы оған пнрпендикуляр жазықтық (ж)-ны жүргізейік.  күшінің (ж)
күшінің (ж)  (
(  )=
)=  =
=  ΔABC (2)
ΔABC (2) Pжh=±2SΔABC (3)
Pжh=±2SΔABC (3) денені ОІ өстен сағат тілі қозғалысына қарсы бағытта айналдыруға тырысады.
денені ОІ өстен сағат тілі қозғалысына қарсы бағытта айналдыруға тырысады. ×
×  (4)
(4) )=npl
)=npl  (7)
(7) )
) 
 ,
,  ,
,  Oxyz координаттар өстерінің бірлік векторлары.
Oxyz координаттар өстерінің бірлік векторлары. )= xY-yX
)= xY-yX =
=  2
2 =
=  ,
,  =
=  ,
,  =
=  болады.
болады. (2)
(2)
 (3)
(3)
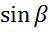 анықталады.
анықталады.  мен
мен 


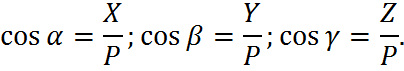
 бас векторы осы күштерден тұрғызылған күштер көпбұрышының тұйықтаушы қабырғасы болғандықтан (1.12 ә) суретті қараңыз),
бас векторы осы күштерден тұрғызылған күштер көпбұрышының тұйықтаушы қабырғасы болғандықтан (1.12 ә) суретті қараңыз),  .
. нөлге тең болу үшін бір мезгілде
нөлге тең болу үшін бір мезгілде  болуы керек, яғни осы күштердің координата өстеріне проекцияларының қосындысы нөлге тең. Сондықтан, кеңістіктегі жинақталатын күштер жүйесінің қажет және жеткілікті тепе-теңдік шарттары былай жазылады:
болуы керек, яғни осы күштердің координата өстеріне проекцияларының қосындысы нөлге тең. Сондықтан, кеңістіктегі жинақталатын күштер жүйесінің қажет және жеткілікті тепе-теңдік шарттары былай жазылады: (1.)
(1.) (2.)
(2.)
 жинақталатын күштер жүйесін (1.11 а) сурет) қарастырайық.
жинақталатын күштер жүйесін (1.11 а) сурет) қарастырайық. және
және  күштерін олардың
күштерін олардың  тең әсерлі күшімен алмастырамыз:
тең әсерлі күшімен алмастырамыз:  .
. күшін
күшін  тең әсерлі күшімен алмастырамыз:
тең әсерлі күшімен алмастырамыз: .
. . (1)
. (1) деп белгілейміз. Осы күштің ұшынан
деп белгілейміз. Осы күштің ұшынан  деп белгіленген күшті көшіреміз. Дәл осылай етіп
деп белгіленген күшті көшіреміз. Дәл осылай етіп  күштерін көшіреміз.
күштерін көшіреміз.
 . (2)
. (2) . (3)
. (3) . (4)
. (4) (5)
(5) (6)
(6) (7)
(7)
 деп, ал олардың түсу нүктелерін А және В деп белгілейік (1-сурет ).
деп, ал олардың түсу нүктелерін А және В деп белгілейік (1-сурет ).  және
және  куштері орналасқан (ж) жазықтығы қос күштің әсер ету жазықтығы ретінде қабылданады.Мұндағы күштердің әсер ету сызықтарының арақашықтығы ,қос күштің иіні ретінде алынады да h әрпімен белгіленеді.Күштердің мәндері тең Р= Р’ ,бағыттары қарама –қарсы болғанымен , әртүрлі екі нүктеге әсер ететіндіктен қос күш нөлге эквивалент жүйе болмайды. *1-сурет
куштері орналасқан (ж) жазықтығы қос күштің әсер ету жазықтығы ретінде қабылданады.Мұндағы күштердің әсер ету сызықтарының арақашықтығы ,қос күштің иіні ретінде алынады да h әрпімен белгіленеді.Күштердің мәндері тең Р= Р’ ,бағыттары қарама –қарсы болғанымен , әртүрлі екі нүктеге әсер ететіндіктен қос күш нөлге эквивалент жүйе болмайды. *1-сурет
 ,бір тең әсерлі күшке келтірілмейді.Оның әсерінен еркін қатты дене тыныштыұ күйінен шығып , айналмалы қозғалыс жасайды.Қос күш бұдан кейін өзгермейтін жүйе.Ол статикада күшпен қатар қарастырылатын жек элемент,негізгі ұғым ретінде алынады.Өзі әсер ететін қатты денені айналдыруға тырысады.Оның айналдырушы әсерін сипаттайтын үш түрлі анықтаушы жағдайлар бар. Біріншіден, ол күшпен иін көбейтіндісіне тең Рh шаманың мөлшері, екіншіден қос күштің әсер ету жазықтығының кеңістікте орналасу жағдайлары, үшіншіден , осы жазықтықтағы қос күштің айналыс бағыты. Міне осы үш сипаттаушы жағдайларды түгел қамтитындай қортынды ұғым көрсетуіміз керек.Ол қос күш моменті туралы ұғым. Қос күш моменті.Қос күш әсері қос күш моментімен анықталады.Моменті, қос күш айналдырушы әсерінің жоғарыда айтылған уш түрлі сипаттамасын түгел қамтитындай етіп анықтаумыз керек.Сондықтан да қос күш моментіне векторлық анықтама беруге тиістіміз.Қос күш моменті деп модулі оның күшімен иінінің көбейтіндісіне (Ph) тең , векторының бағытын анықтауда оң бұранда ережесі қолданылады(1-сурет).Қос күш моментінің векторын
,бір тең әсерлі күшке келтірілмейді.Оның әсерінен еркін қатты дене тыныштыұ күйінен шығып , айналмалы қозғалыс жасайды.Қос күш бұдан кейін өзгермейтін жүйе.Ол статикада күшпен қатар қарастырылатын жек элемент,негізгі ұғым ретінде алынады.Өзі әсер ететін қатты денені айналдыруға тырысады.Оның айналдырушы әсерін сипаттайтын үш түрлі анықтаушы жағдайлар бар. Біріншіден, ол күшпен иін көбейтіндісіне тең Рh шаманың мөлшері, екіншіден қос күштің әсер ету жазықтығының кеңістікте орналасу жағдайлары, үшіншіден , осы жазықтықтағы қос күштің айналыс бағыты. Міне осы үш сипаттаушы жағдайларды түгел қамтитындай қортынды ұғым көрсетуіміз керек.Ол қос күш моменті туралы ұғым. Қос күш моменті.Қос күш әсері қос күш моментімен анықталады.Моменті, қос күш айналдырушы әсерінің жоғарыда айтылған уш түрлі сипаттамасын түгел қамтитындай етіп анықтаумыз керек.Сондықтан да қос күш моментіне векторлық анықтама беруге тиістіміз.Қос күш моменті деп модулі оның күшімен иінінің көбейтіндісіне (Ph) тең , векторының бағытын анықтауда оң бұранда ережесі қолданылады(1-сурет).Қос күш моментінің векторын  (
(  =Ph=P’h (1)
=Ph=P’h (1) =
=  =Ph (2)
=Ph (2) (
(  х
х  немесе
немесе 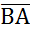 х
х 
 = Ph (3)
= Ph (3) х
х  ) векторы мен қос үш моментінің векторы
) векторы мен қос үш моментінің векторы 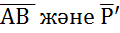 векторларының векторлық көбейтіндісімен өрнектей аламыз.
векторларының векторлық көбейтіндісімен өрнектей аламыз. (
( 
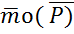 +
+  ) =
) =  Aх
Aх  ) (7)
) (7) A
A  (
(  A
A  ≠0,
≠0,  0 = 0 шарттары орындалған жағдайда теңәсерлі бір күшке келтіріледі.Бұл жағдайдағы күштердің жазық жүйесіне Вариньон теоремасын қолдануға болады.
0 = 0 шарттары орындалған жағдайда теңәсерлі бір күшке келтіріледі.Бұл жағдайдағы күштердің жазық жүйесіне Вариньон теоремасын қолдануға болады. n) күштердің жазық жүйесі О*келтіру центрінде бір теңәсерлі
n) күштердің жазық жүйесі О*келтіру центрінде бір теңәсерлі  l және оның әсер ету сызығы О* нүктесін басып өтеді(3-сурет).
l және оның әсер ету сызығы О* нүктесін басып өтеді(3-сурет). 
 i) десек,онда Вариньон теор-сын мына теңдікпен өрнектеуге болады:
i) десек,онда Вариньон теор-сын мына теңдікпен өрнектеуге болады:  =
=  i).*
i).* .осыдан 1кГ=9,81 Н
.осыдан 1кГ=9,81 Н