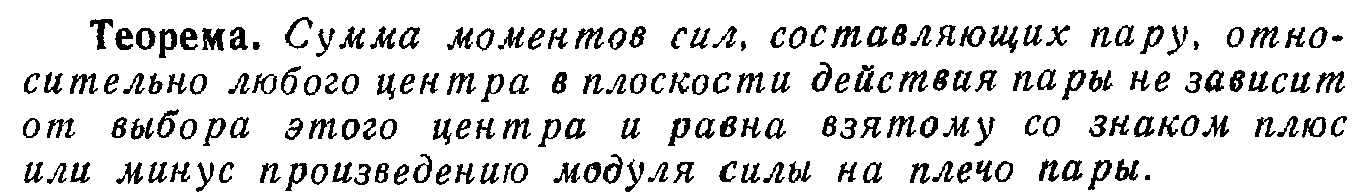ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Теорема о сумме моментов сил пары.
Основные типы реакции связей.
4.Приведение системы сходящихся сил к равнодействующей.
5. Условия равновесия сходящихся сил.
Теорема о трех силах. (с.21) Если абсолютно твердое тело находится В равновесии под действием плоской системы Трех непараллельных сил, то линии их действия Пересекаются в одной точке.
Алгебраический и векторный момент силы относительно точки. Алгебраическим моментом силы относительно точки (или центра) называется взятое со знаком плюс или минус произведение модуля силы на плечо (рисунок 1.2). Знак плюс выбирается в том случае, если сила стремится поворачивать плоскость относительно центра момента против хода часовой стрелки. Моментом силы относительно точки (рисунок 1.1) называется векторное произведение радиус-вектора точки приложения силы на вектор силы. Mo(F) = r ⊗ F Момент силы относительно оси.
Момент силы относительно оси, например Oz (рисунок 1.18), равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси (F' ) относительно точки пересечения оси с плоскостью, т.е.
Mz(F) = Mo(F') = F' h'. 9.Связь момента силы относительно оси с векторным моментом силы относительно точки
Проведем через точку O, где задан момент силы относительно точки Mo(F) декартовы оси координат x, y, z (рисунок 1.4). Момент силы относительно точки можно представить в виде суммы трех векторов Mo(F) = Mx(F)i + My(F)j + Mz(F)k. .
Рисунок 1.4 Эти вектора являются моментами силы относительно осей x, y, z: Mx(F) = |Mo(F)|cos(i, Mo(F)), My(F) = |Mo(F)|cos(j, Mo(F)), Mz(F) = |Mo(F)|cos(k, Mo(F)), Момент силы относительно оси равен проекции на эту ось момента силы относительно любой точки на оси. Пара сил. Алгебраический и векторый момент пары сил. Па́ра сил — совокупность двух сил, которые приложены к одному абсолютно твёрдому телу и при этом равны по модулю и противоположны по направлению. Алгебраическим моментом пары сил называют взятое со знаком плюс или минус произведение одной из сил пары на плечо пары сил. Векторный момент пары сил - вектор, модуль которого равен произведению модуля силы пары на ее плечо. Векторный момент пары сил направлен перпендикулярно плоскости действия пар сил так, чтобы с его направления можно было видеть стремление пары вращать тело против хода часовой стрелки. Алгебраический момент пары силВекторный момент пары сил, лежащих в плоскости Oxy, также направлен вдоль оси Oz, поскольку он равен векторному моменту одной из сил относительно точки приложения другой силы. Поэтому момент пары сил в этом случае также можно рассматривать как алгебраическую величину. Алгебраический момент пары сил равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары: M=±F·d.Правило знаков моментов пар сил аналогично правилу для моментов сил.
Т. Об эквивалентоности пар сил, расположенных в одной плоскости. Две пары, лежащие в одной плоскости и имеющие равные по величине и по знаку моменты, эквивалентны.
Теорема о сумме моментов сил пары. Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.
|