 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ДЕФОРМАЦИЯ МЕН ОРЫН АУЫСТЫРУ
Қандай дене болмасын сыртқы күш әсерінен өздерінің өлшемдері мен формаларын өзгертеді, деформацияланады. Дененің сызықты өлшемдерінің өзгеруі сызықтық деформация, ал бұрыштық өлшемдерінің өзгеруі бұрыштық деформация делінеді. Деформация нәтижесінде дененің сызықтық өлшемінің өcyi – созылу (ұзару), ал кемуі – сығылу (қысқару) деп аталады. Деформация материалдың атомдарының ара қашықтықтарының өзгеруі мен атом блоктарының орын ауыстыруы салдарынан туады. Оның табиғатын толық зерттеп білу үшін, жазық дененің кез келген нүктесінің жанынан өзара перпендикуляр АВ, СA түзулерін алайық (I. 3, а-сурет). Дене деформацияланғанда АС түзу сызығы шамасына ұзарады (I. 3, б-сурет). Оның орташа сызықтық салыстырмалы деформациясы келесі формуламен анықталады.
1.3-сурет
Енді бұрыштық деформацияны қарастырайық. Деформацияға дейінгі ВАС тікбұрышы мен деформациядан кейінгі В'А'С сүйір бұрышының арасындағы айырма берілген нүктенің бұрыштық деформациясын сипаттайды. Сонымен күш түскен дененің кез келген нүктедегі деформациясы сызықтық салыстырмалы және бұрыштық деформациялармен сипатталады. Денеде пайда болған сызықтық және бұрыштық деформациялар сырттан әсер етуші күш жойылғанда толық жойылуы немесе жойылмауы да мұмкін. Сыртқы күш әсері жойылғанда, денедегі деформация да жойылса, ондай деформацияны серпімді деп, ал деформация толық жойылмай қалса, онда қалдық деформацияны пластикалық деформация деп атайды. Егер дененің бекіту шарттары мен нүктелеріндегі деформацияның шамасы белгілі болса, онда кез келген нүктенің деформациядан кейінгі орнын, яғни орын ауыстыру шамасын анықтауға болады. Машина бөлшектері серпімді деформацияланғанда ғана, олардың жұмыс істеу қабілеті қамтамасыз етіледі. Сондықтан, нүктелердің ең үлкен орын ауыстыру шамасы белгілі бip мүмкіндік шамадан аспауы керек. Мұндай шарт теңсіздік ретінде көрсетіліп, қатаңдық шарты деп аталады.
7 – сұрақ
1.5-сурет нүктесіндегі ішкі күштің орташа шамасын – орташа кернеуді аңықтайды.
Шексіз кіші аудан нөлге ұмтылғандағы көрсетілген қатынастың шегі В нүктесіндегі толық кернеу деп аталады:
Толық кернеудің көлденең қима жазықтығына перпендикуляр OZ өсте, түсіріген проекциясы тік кернеудеп аталып, OZ әрпімен белгіленеді, ал қима бетіне түcipiлгeн проекциясы жанама кернеудеп
1.6-сурет
Суреттен, толық кернеу
8 – сұрақ ПАРАЛЛЕЛЬ ӨСТЕРГЕ ҚАРАҒАНДА ИНЕРЦИЯ МОМЕНТЕРІНІҢ АРАСЫНДАҒЫ ТӘУЕЛДІЛІК Қиманың өзара перпендикуляр X, У центрлік өстеріне қарағандағы
инерция моменттері белгілі дейік. Енді осы өстерге параллель жаңа Фигураның
Бұл өрнектердегі өстеріне қарағандағы статикалық моменттер болғандықтан нөлге тең, олай болса:
Сонымен, фигураның кез келген центрлік өсіне параллель өске қарағандағы өстік инерция моменті, центрлік өстік инерция моментіне, фигураның ауданын осы өстердің ара қашықтығының квадратына көбейтіп қосқанға тең. Центрлік өске қарағандағы өстік инерция моменті, осы өске параллель, кез келген өске қарағандағы өстік инерция моменттерінен кіші. Фигураның өзара перпендикуляр центрлік өстеріне параллель өстерге қарағандағы центрден тепкіш инерция моменті, фигура ауданының осы өстердің ара қашықтықтарына көбейтіп қосқанға тең (5.4-сурет). Жалпы жағдайда, күрделі фигуралардың инерция моменттері келесі формулалармен анықталады
15 – сұрақ БҰРЫЛҒАН ӨСТЕРГЕ ҚАРАҒАНДАҒЫ ИНЕРЦИЯ МОМЕНТТЕРІНІҢАРАСЫНДАҒЫ БАЙЛАНЫС Қиманың ауырлық центрі арқылы өтетін өзара, перпендикуляр X, У өстеріне қарағандағы инерция моментері белгілі болсын (5.5-сурет).
Енді қиманың осы өстерге
Ол үшін
Алынған 5.08 және 5.09 өрнектерін қоссақ Яғни, өзара перпендикуляр өстерге қарағандағы инерция моменттерінің қосындысы, осы өстерді кез келген біp бұрышқа бұрғаннан өзгермей, тұрақты болып қалады. Енді, өстік инерция моменттерінің айырмасын қарастырсақ
өзара перпендикуляр өстерге қарағандағы өстік инерция моменттерінің айырмасы, осы өстерге қарағандағы центрден тепкіш инерция моментінің шамасына тең екенін көреміз.
11 – сұрақ ИНЕРЦИЯНЫҢ БАС ӨCTEPI, БАС MOMEHTTEPI
Алдыңғы параграфта алынған 5.08, 5.09, 5.10 формулаларына қарап инерция моменттерінің тек
осыдан
Алынған формула бойынша бұрышының екі мәні бар: біpі ao екіншісі Енді 5.08 және 5.09 өрнектеріндегі
Өрнектерді тригонометриялық функциялардан босатып басты инерция моментерінің формулаларын келесі түрге келтіруге болады
Өстік инерция моменті мен қима ауданының арасындағы байланыс арқылы табылатын шаманы
қиманың инерция радиусы деп атайды. Жарты өстері бас инерция радиустеріне тең (
Инерция эллипсінен кез келген центрлік өске карағандағы инерция моментін табуға болады. Мысалы, Xi өсіне қарағандағы инерция моментін табу үшін, осы өске параллель эллипске жанама жүргізіледі. Эллипс центрінен жанамаға түсірілген перпендикулярдың (СА) ұзындығы инерция радиусының (ix) шамасына тең (5. 9-сурет). Инерция радиусы арқылы, инерция моментін келесі формуламен анықтауға болады
16 – сұрақ ТАРАЛҒАН КҮШТІҢ ҚАРҚЫНДЫЛЫҒЫ, ЖАНАМА КҮШ, ИЮ МОМЕНТІ АРАЛАРЫНДЫҒЫ ДИФФЕРЕНЦИАЛДЫҚ БАЙЛАНЫС
Бip қалыпты таралған күштің қарқындылығы, жанама күш, ию моменті аралағындағы дифференциалдық байланыстарды анықтау үшін 6.4-суреттегі арқалықты қарастырайық. Сол жақтағы А тірегінен z қашықтығында жатқан көлденең қимада пайда болатын жанама күштің өрнегі
ал
Соңғы 6.03 теңдеуінен 6.02 теңдеуін алып
екенін көреміз. Демек, кез келген қимадағы жанама күштің өрнегінен z бойынша алынған бірінші туынды, сол аралықтағы әсер етуші бip қалыпты таралған күштің қарқындылығына тең. Абсциссасы
ал абсциссасы z+dz-ке тең көлденең қимадағы ию моментінің өрнегі
Соңғы (6.06) теңдігінен (6.05) теңдігін алып
екенін көреміз. Демек, кез келген көлденең қимадағы ию моментінің өрнегінен z бойынша алынған бірінші туынды, осы қимадағы жанама күшке тең. Олай болса
Көлденең қимадағы ию моментінің өрнегінен z бойынша алынған екінші туынды осы аралықта әсер етуші бip қалыпты , таралған күштің қарқындылығына тең. Алынған 6.04, 6.07, 6.08 теңдіктер жанама күш, ию моменті, таралған күштің қарқындылығы аралағындағы дифференциалдық байланыстар деп аталады. . ЖАНАМА КҮШ ПЕН ИЮ MOMEHTІ Қос терікті иілген арқалықтың көлденең қималарындағы ішкі күштерді анықтайық . Кез келген т-т қимасындағы ішкі күштерді табу үшін, қию әдесі бойынша, сол қима арқылы арқалықты екіге бөліп, біp бөлігін алып тастаймыз. Алып тасталынған бөліктің қалған бөлікке әсерін көлденең күш пен ию моментімен алмастырамыз. Қалған бөлік сыртқы күштер мен ішкі күштердің әсерінен тепе-теңдік күйде болуы тиіс. Статиканың бірінші теңдеуі
яғни кез келген т-т қимасындағы көлденең күш Q(z), сол қиманың біp жағында әсер етуші сыртқы күштердің У өсіне түсірілген проекцияларының алгебралық қосындысына тең. Статиканың екінші тендеуі
осыдан Яғни, кез келген т-т қимасындағы ию моменті М( 6.2-сурет Бір қалыпты таралған күштерді Көлденең күш пен ию моментінің таңбалары туралы келесі ережелер қабылданады. Көлденең т-т қимасының сол жағында әсер eтiп тұрған сыртқы күштердің қорытынды күші (R) төменнен жоғары қарай ал оң жақтағы сыртқы күштердің қорытынды күші (R) жоғарыдан төмен қарай бағытталған болса, ол қимадағы жанама күш Q(z) оң таңбалы болып саналады. Кері жағдайда жанама теріс таңбалы. Көлденең
ЖАНАМА КҮШ ПЕН МОМЕНТІНІҢ ЭПЮРЛЕРІН ТҰРҒЫЗУ Ию моменті мен жанама күштің бойлық өс бойымен өзгеру заңдылығын көрсету үшін олардың эпюрлері тұрғызылады. Эпюрлерді тұрғызу тәртібі келесі мысалда көрсетілген. 6.1-мысал. Берілген арқалық үшін Шешуі. 1.Тірек реакцияларын анықтау. Тіректердің реакцияларын анықтау үшін оларды 5.6-сурет
Жылжымайтын тіректің
бағытын кері өзгерту керек екенін көрсетеді. Дәл осылай,
Жылжымалы тіректің
Егер аралықтың (раманың) бір ұшы қатаң бекітіліп, екінші ұшы бос болса, тірек реакцияларын (  анықтау қажетсіз болар еді. Өйткені, аралықтардағы ішкі күштерді бос ұшынан бастап анықтауға болады. анықтау қажетсіз болар еді. Өйткені, аралықтардағы ішкі күштерді бос ұшынан бастап анықтауға болады. 2. Көлденең күштер мен ию моменттерін анықтау. Аралықтың көлденең күштері мен ию моменттері тұрақты заңдылықтармен өзгеретін бөлігі аралық деп аталады. Сыртқы қадалған күштер моменттер әсер етіп тұрған қималар таралған күштердің әсері басталған немесе аяқталған жерлеріне сәйкес келетін қималар аралықтардың шекараларын анықтайды. Берілген аралық рим цифрларымен белгіленген үш аралықтан тұрады. Бірінші аралық;
Бірінші аралықта Екінші аралық;
Екінші аралықта да Үшінші аралық
Үшінші аралықта жанама күш оң таңбасын теріс таңбаға ауыстырады. Демек, қандай да бір қимада жанама күш нөлге тең
мұндағы Жанама күш пен ию моментінің арасындағы дифференциалдық байланысты ескерсек
Енді, аралықтың бойлық өсіне параллель өстер жүргізіп, осы өстерге, қималардағы
20 – сұрақ АУМАЛЫ КҮШ. ЭЙЛЕР ФОРМУЛАСЫ
Сығушы күштің шамасы аумалы күшке теңелгенде арқалық орнықтылығын жоғалтпай, шамалы иіліп, талғаусыз тепе-теңдік күйде болады (7.2, а-сурет). Ию моментінің таңбалары туралы ереже бойынша, иілген арқалықтың дөңес жағы жоғары жатса, оның қималарындағы ию 7.1-сурет моменттері теріс, иілу мөлшерлері оң таңбалы, ал дөңес жағы төмен жатса, ию моменті оң, иілу мөлшері теріс таңбалы. Олай болса, координаты
Арқалық серпімді деформацияланады деп, серпімді сызығының, дифференциалдық тендеуін құрайық:
Енді деп белгілейік. Сонда 7.02 теңдеуін келесі түрде жазуға болады.
Бұл сызықты дифференциалдық. теңдеудің шешімі
Мұндағы А және В — тіректердегі келесі шарттарды қанағаттандыратын интегралдық тұрақты шамалар.
Бірінші шарт бойынша А=0, өйткені cos
Екінші шарт бойынша
Алынған 7.03, 7.06 теңдіктерін салыстырып
Сығылған арқалық орнықтылығын ең кiшi қатаңдық жазықтығында жоғалтады, олай болса
Енді стреженьнің орнықты тепе-тендік күйінен ауытқуына сәйкес, аумалы күштің ең кіші мәнін табайық..
Бұл шешім есептің бастапқы шартына қайшы, демек аумалы күш
Бұл формуланы 1744 жылы Петербург академиясының академигі Л.Эйлер формуласы деп атайды. Егер 7.05, 7,06 теңдеулерін бірге қарастырсақ, сығылған арқалықтың серпімді сызығы келесі теңдеумен өрнектеледі:
Соңғы теңдеуден
Косинустың ең кіші мәніне сәйкес аргумент
арқалықтың серімді сызығы синусоиданың жарты толқынына сәйкес келеді, ең, үлкен иілу мөлшері ортасында жатады (7.2,а-сурет).
20 – сұрақ Дағдарыс кернеу. Эйлер формуласының қолдану шегі.Бойлық жүктелген стерженьнің кӛлденең қимасында тік кернеу туындайды және оның шамасы жүктеме ӛскен сайын ӛседі. Дағдарыс күшке сәйкес келетін тік кернеуді дағдарыс кернеу деп атайды
19 – сұрақ Ясинский формуласы. Іс жүзінде, кӛптеген конструкция элементтері иілгіштігі шектік мәннен кем стержень болып келеді. Мұндай стержендерді орнықтылыққа есептеудің басқа әдісін Ф.С. Ясинский ұсынды. Алдын-ала кӛптеген зерттеулердің нәтижелерін талдап және кӛптеген материалдардың ау s мен l арасындағы тәуелділікті сызбаша кескіндеп, пропорционалдық шектен үлкен дағдарыс кернеулерді анықтайтын келесі эмпирикалық формуланы қорытып шығарды
мұндағы a,b - материалдарға байланысты, тәжірибе жүзінде анықталатын, қабылданатын тұрақты коэффициенттер. Бұл формуланы Ясин формуласы деп атайды. Кейбір материалдар үшін, a,b коэффициенттері 2.1-кестеде берілген.
|



 (1.01)
(1.01)
 . (1.02)
. (1.02)
 қима арқылы үздіксіз жайыла таралып беріледі Олардың әсер ету заңдылығын білу үшін қима бетінде жатқан
қима арқылы үздіксіз жайыла таралып беріледі Олардың әсер ету заңдылығын білу үшін қима бетінде жатқан 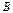 нүктесін қарастырайық (1.5, а-сурет). Нүктені қоршаған шексіз кіші ауданды
нүктесін қарастырайық (1.5, а-сурет). Нүктені қоршаған шексіз кіші ауданды 
 , ал ол ауданға сәйкес келетін ішкі күшті
, ал ол ауданға сәйкес келетін ішкі күшті  деп белгілейік. Ішкі күш
деп белгілейік. Ішкі күш  ның шексіз кіші аудан
ның шексіз кіші аудан  ке қатынасы
ке қатынасы  . (1.04)
. (1.04) . (1.05)
. (1.05)
 ,екендігін көреміз.
,екендігін көреміз.
 өстеріне қарағандағы инерция моменттерінің шамаларын анықтайық (5.4-сурет). Бөлініп алынған
өстеріне қарағандағы инерция моменттерінің шамаларын анықтайық (5.4-сурет). Бөлініп алынған  тің ХОУ жүйесіндегі координаттары х, у, ал
тің ХОУ жүйесіндегі координаттары х, у, ал  жүйесіндегі координаттары
жүйесіндегі координаттары  = x+a,
= x+a,  =y+b болсын.
=y+b болсын.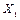 және
және  өстеріне қарағандағы инерция моменттері төмендегі интегралдар мен анықталады
өстеріне қарағандағы инерция моменттері төмендегі интегралдар мен анықталады


 интегралдары, центрлік Х, У
интегралдары, центрлік Х, У . (5.06)
. (5.06)
 (5.07)
(5.07)
 бұрышын жасайтын центрлік
бұрышын жасайтын центрлік  өстеріне қарағандағы инерция моменттерін табайық (өстердің сағат тіліне қарсы бағытта бұрылуы оң деп қабылданған).
өстеріне қарағандағы инерция моменттерін табайық (өстердің сағат тіліне қарсы бағытта бұрылуы оң деп қабылданған).

 -тің берілген ХО
-тің берілген ХО  жүйеciндeгi координаттары мен жаңа Х1ОУ1 жүйесіндегі координаттарының арасындағы өзара байланысты анықтайық
жүйеciндeгi координаттары мен жаңа Х1ОУ1 жүйесіндегі координаттарының арасындағы өзара байланысты анықтайық Олай болса
Олай болса 






 (5.08)
(5.08) (5.09)
(5.09) (5.10)
(5.10) екенін көреміз.
екенін көреміз.

 (5.11)
(5.11) 90°; демек инерция моменттерінің мәні экстремальды өзара перпендикуляр екі-ақ өс бар. Бұл өстер бас өстер деп аталады, оларға қарағандағы өстік инерция моменттері бас инерция моменттері деп аталады. Бас өстерге қарағандағы центрден тепкіш инерция моменті нөлге тең.
90°; демек инерция моменттерінің мәні экстремальды өзара перпендикуляр екі-ақ өс бар. Бұл өстер бас өстер деп аталады, оларға қарағандағы өстік инерция моменттері бас инерция моменттері деп аталады. Бас өстерге қарағандағы центрден тепкіш инерция моменті нөлге тең. қойып, бас инерция моменттерің анықтаймыз (5.5-сурет).
қойып, бас инерция моменттерің анықтаймыз (5.5-сурет).
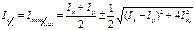 . (5.12)
. (5.12) ,
,
 ), бас өстерге тұрғызылған эллипс – инерция эллипсі деп аталады, келесі теңдеумен өрнектеледі
), бас өстерге тұрғызылған эллипс – инерция эллипсі деп аталады, келесі теңдеумен өрнектеледі
 .
. , (6.02)
, (6.02)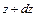 қашықтығында жатқан көлденең қимадағы жанама күштің өрнегі
қашықтығында жатқан көлденең қимадағы жанама күштің өрнегі (6.03)
(6.03)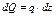 немесе
немесе  (6.04)
(6.04) -ке тең көлденең қимадағы ию моменті
-ке тең көлденең қимадағы ию моменті (6.05)
(6.05)
 (6.06)
(6.06) (6.07)
(6.07) (6.08)
(6.08) осыдан
осыдан 


 қимасының сол жағындағы әсер етуші сыртқы күштердің осы қиманың ауырлық центріне қарағандағы қорытынды моменті (М) сағат тілімен бағыттас, ал оң жағындағы күштердің қорытынды моменті сағат тіліне қарсы бағытта болса, ол қимадағы ию моменті оң таңбалы деп саналады (6. 3, а-сурет). Kepi жағдайда ию моменті M(z) теріс таңбалы (6. 3, б-сурет).
қимасының сол жағындағы әсер етуші сыртқы күштердің осы қиманың ауырлық центріне қарағандағы қорытынды моменті (М) сағат тілімен бағыттас, ал оң жағындағы күштердің қорытынды моменті сағат тіліне қарсы бағытта болса, ол қимадағы ию моменті оң таңбалы деп саналады (6. 3, а-сурет). Kepi жағдайда ию моменті M(z) теріс таңбалы (6. 3, б-сурет).

 мен
мен  эпюрлерін тұрғызыңыз (6.5,a-сурет).
эпюрлерін тұрғызыңыз (6.5,a-сурет). өстерімен бағыттас деп қарастырып, статиканың 6.01 теңдеулерін пайдаланамыз.
өстерімен бағыттас деп қарастырып, статиканың 6.01 теңдеулерін пайдаланамыз. Бойлық өс бойымен әсер етуші сыртқы күш жоқ болғандықтан, А тірегіндегі реакцияның горизонталь құраушысы
Бойлық өс бойымен әсер етуші сыртқы күш жоқ болғандықтан, А тірегіндегі реакцияның горизонталь құраушысы  нөлге тең.
нөлге тең.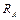 реакциясын анықтау үшін, жылжымалы тіректің топсасына қарағандағы сыртқы күштердің моменттерін нөлге теңестіреміз.
реакциясын анықтау үшін, жылжымалы тіректің топсасына қарағандағы сыртқы күштердің моменттерін нөлге теңестіреміз.
 реакциясын анықтаймыз.
реакциясын анықтаймыз.

 теңдеуінің орнына басқа
теңдеуінің орнына басқа  теңдеуін пайдалануға болады. Көбінесе,
теңдеуін пайдалануға болады. Көбінесе, 


 мұндағы
мұндағы  координат басынан ішкі күштер анықталатын қимаға дейінгі ара қашықтық, индексі аралық номерін көрсетеді. Жанама күш пен ию моментінің анықтамалары мен таңбалары туралы ережеге сүйеніп, олардың өрнектерін құрамыз (6.5,б-сурет).
координат басынан ішкі күштер анықталатын қимаға дейінгі ара қашықтық, индексі аралық номерін көрсетеді. Жанама күш пен ию моментінің анықтамалары мен таңбалары туралы ережеге сүйеніп, олардың өрнектерін құрамыз (6.5,б-сурет).
 болғанда,
болғанда, 
 болғанда,
болғанда, 
 -ге тәуелсіз тұрақты шама, ал
-ге тәуелсіз тұрақты шама, ал  ге тәуелді сызықтық функция.
ге тәуелді сызықтық функция. (6.5,в-сурет).
(6.5,в-сурет).

 болғанда
болғанда 
 тұрақты шама,
тұрақты шама,  сызықты функция.
сызықты функция. (6.5, г-сурет). Үшінші аралықтың
(6.5, г-сурет). Үшінші аралықтың 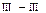 қимасындағы ішкі күштерді анықтау үшін, қима әдісі бойынша аралықты осы қима арқылы екіге бөліп, оң немесе сол жақ бөліктерінің тепе-теңдік күйін қарастыруға болады. Сол бөлігінің оң бөлігіне қарағанда сыртқы күш факторлары көп болғандықтан,статикалық теңдеулері де күрделі. Сондықтан, ішкі күштерді оң бөлігінің тепе-теңдік теңдеулерінен анықтаған ыңғайлы.
қимасындағы ішкі күштерді анықтау үшін, қима әдісі бойынша аралықты осы қима арқылы екіге бөліп, оң немесе сол жақ бөліктерінің тепе-теңдік күйін қарастыруға болады. Сол бөлігінің оң бөлігіне қарағанда сыртқы күш факторлары көп болғандықтан,статикалық теңдеулері де күрделі. Сондықтан, ішкі күштерді оң бөлігінің тепе-теңдік теңдеулерінен анықтаған ыңғайлы.

 болғанда,
болғанда, 
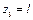 болғанда,
болғанда, 
 ке тәуелді сызықты функция, ал
ке тәуелді сызықты функция, ал  квадратты парабола заңдылығымен өзгереді.
квадратты парабола заңдылығымен өзгереді. осыдан
осыдан
 арлықтың оң ұшынан жанама күш нөлге тең қимаға дейінгі ара қашықтық.
арлықтың оң ұшынан жанама күш нөлге тең қимаға дейінгі ара қашықтық. 

 үшінші аралықтың қималарындағы ию моменттерінің ең үлкен екенін көреміз.
үшінші аралықтың қималарындағы ию моменттерінің ең үлкен екенін көреміз. тің табылған мәндері белгілі бір масштабпен перпендикуляр бағытта өлшеп саламыз.Табылған нүктелерді қосып, жанама күш пен ию моментінің эпюрлерін аламыз (6.5, д,е-сурет).
тің табылған мәндері белгілі бір масштабпен перпендикуляр бағытта өлшеп саламыз.Табылған нүктелерді қосып, жанама күш пен ию моментінің эпюрлерін аламыз (6.5, д,е-сурет). . (7.01)
. (7.01) немесе
немесе  (7.02)
(7.02) (7.03)
(7.03) (7.04
(7.04
 болса,
болса,  ,z = l болса, у=0
,z = l болса, у=0 sin
sin  = 0. Олай болса,
= 0. Олай болса, (7.05)
(7.05) . Егер
. Егер  ,
,  , яғни
, яғни  осыдан
осыдан немесе
немесе  (7.06)
(7.06) екенін көреміз.
екенін көреміз.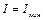 , яғни
, яғни . (7.07)
. (7.07)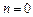 болса
болса 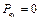 .
. болғанда өзінің ең кіші мәніне ие болады
болғанда өзінің ең кіші мәніне ие болады (7.08)
(7.08) болса
болса 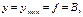 яғни
яғни (7.09)
(7.09)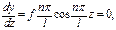 мұндағы
мұндағы  олай болса,
олай болса, 
 болғандықтан,
болғандықтан, осыдан
осыдан  (7.10)
(7.10)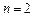 болса
болса  болса,
болса,  . Яғни, тірек аралығындағы синусоидалық жарты толқындардың саны
. Яғни, тірек аралығындағы синусоидалық жарты толқындардың саны  -ге тең (7.2,б, в-сурет).
-ге тең (7.2,б, в-сурет).