ЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕ
АААААААААААААААААААААААА Анықтауыштар. Анықтауыштардың қасиеттері.Анықтама.  саны екінші ретті анықтауыш деп аталады да, мына түрде жазылады: саны екінші ретті анықтауыш деп аталады да, мына түрде жазылады: 
Анықтауыштың қасиеттері. 1-қасиет. Анықтауыштың жолдарын сәйкес бағандармен алмастырсақ, онда оның шамасы өзгермейді.2-қасиет. Егер анықтауыштың жолдарының орнын ауыстырсақ, онда оның таңбасы өзгереді.3-қасиет. Егер анықтауыштың кейбір жолының немесе бағанының барлық элементтері нөл болса, онда анықтауыштың шамасы нөлге тең. 4-қасиет. Егер анықтауыштың кейбір жолының элементтерін k санына көбейтсек, онда анықтауыштың шамасы да осы k санына көбейтіледі. Яғни, жолының немесе бағанының ортақ көбейткішін анықтауыштың таңбасының алдына шығаруға болады. 5-қасиет.Егер анықтауыштың екі жолдарының элементтері пропорционал болса, онда анықтауыш нөлге тең.6-қасиет.Анықтауыштың қайсібір жолының элементтеріне басқа жолдың элементтерін бірдей k санына көбейтіп қосқаннан, анықтауыштың шамасы өзгермейді.7-қасиет.Егер анықтауыштың қайсібір жолы (бағаны) екі санның қосындысынан тұрса, онда бұл анықтауыш екі анықтауыштың қосындысына тең. Алгебралық сызықтық теңдеулер жүйесі. Үйлесімді, үйлесімсіз, анықталған ж/е анықталмағын жүйелер. Кронекер-Капеллдің теоремасы. Сызықты теңдеулер жүйесiнің негізгі ұғымдары.  белгiсiздерi бар белгiсiздерi бар 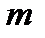 теңдеулерден тұратын сызықты жүйе деп, мынандай теңдеулер жүйесiн айтады ( 1) теңдеулерден тұратын сызықты жүйе деп, мынандай теңдеулер жүйесiн айтады ( 1)   теңдеулер жүйесiнiң коэффициенттерi, теңдеулер жүйесiнiң коэффициенттерi,   жүйенiң бос мүшелерi, Ең кемiнде бiр шешiмi бар теңдеулер жүйесiн үйлесiмдi,ал шешiмi жоқ теңдеулер жүйесiн үйлесiмсiздеп атайды. Тек қана бiр ғана шешiмi бар жүйенi анықталған, ал бiрден артық шешiмi бар жүйенi анықталмаған деп атайды. Егер барлық жүйенiң бос мүшелерi, Ең кемiнде бiр шешiмi бар теңдеулер жүйесiн үйлесiмдi,ал шешiмi жоқ теңдеулер жүйесiн үйлесiмсiздеп атайды. Тек қана бiр ғана шешiмi бар жүйенi анықталған, ал бiрден артық шешiмi бар жүйенi анықталмаған деп атайды. Егер барлық  болса, онда (1) жүйе бiртектi, ал ең болмағанда бос мүшелердiң бiреуi нөлге тең болмаса ол бiртектi емес деп аталады. болса, онда (1) жүйе бiртектi, ал ең болмағанда бос мүшелердiң бiреуi нөлге тең болмаса ол бiртектi емес деп аталады. -Анықталмаған интеграл ұғымы. Қасиеттері.Анықтама. (а,в) интервалындағы  функцияның алғашқы функцияларының функцияның алғашқы функцияларының  жиынын жиынын  функцияның анықталмаған интегралы деп атайды да, функцияның анықталмаған интегралы деп атайды да,  символымен белгілейді. Анықталмаған интегралдың қасиеттері. символымен белгілейді. Анықталмаған интегралдың қасиеттері. 1.  , ,  2.  1 1 3.  , ,  4. Егер  функциясы функциясы  функцияның алғашқы функциясы болса, онда функцияның алғашқы функциясы болса, онда  , ,
Анықталмаған интегралдарды тікелей интегралдау, алмастыру н/е айнымалыны ауыстыру ж/е бөліктеп интегралдау әдістері.1) Тікелей интегралдау әдісі. Анықталмаған интегралды оның анықтамасының, қасиеттерінің және интегралдар кестесінің көмегімен интегралдауды тікелей интегралдау әдісі деп атайды. Егер бұл әдіс арқылы интегралдау мүмкін болмаса басқа әдістер қолданылады. 2) Алмастыру немесе айнымалыны ауыстыру әдісі.  . .
3)Бөліктеп интегралдау әдісі.  , Айнымалылары бойынша біртекті дифференциалдық теңдеулер. Бірінші ретті сызықтық дифференциалдық теңдеулер. , Айнымалылары бойынша біртекті дифференциалдық теңдеулер. Бірінші ретті сызықтық дифференциалдық теңдеулер.
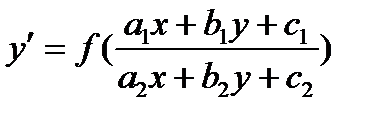 теңдеуін біртекті теңдеуге келтіру үшін теңдеуін біртекті теңдеуге келтіру үшін  , ,  деп алып жаңа деп алып жаңа  және және  айнымалыларын енгізу керек, мұндағы айнымалыларын енгізу керек, мұндағы 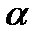 және және  белгісіз сандарды берілген теңдеу біртекті болатындай етіп табу керек. Яғни олар белгісіз сандарды берілген теңдеу біртекті болатындай етіп табу керек. Яғни олар 
теңдеулер жүйесінің шешімі болуға тиіс. Бірінші ретті сызықтық дифференциалдық теңдеулер. Бірінші ретті сызықты дифференциалдық теңдеу деп, белгісіз  фкнкция мен оның туындысы фкнкция мен оның туындысы  сызықты болатын теңдеуді айтады. сызықты болатын теңдеуді айтады.  (8) (8)
Мұндағы  және және   кесіндідегі үзіліссіз функциялар. Егер кесіндідегі үзіліссіз функциялар. Егер  аралығында аралығында  болмаса, онда (8) теңдеуді біртексіз ал болмаса, онда (8) теңдеуді біртексіз ал  болса біртекті сызықты теңдеу деп аталады. болса біртекті сызықты теңдеу деп аталады. а) Лагранж әдісі(тұрақтыны вариациалау әдісі). (8) теңдеуге сәйкес  біртекті теңдеудің жалпы шешімі біртекті теңдеудің жалпы шешімі  , мұндағы с-кез келген тұрақты сан. Тұрақтыны вариациалау әдісі бойынша (8) теңдеудің жалпы шешімін , мұндағы с-кез келген тұрақты сан. Тұрақтыны вариациалау әдісі бойынша (8) теңдеудің жалпы шешімін  түрінде іздейді. түрінде іздейді. 
б) Бернулли әдісі. (8) теңдеудің шешімін екі функцияның көбейтіндісі түрінде іздейді:  , онда , онда  . .  және және  -терді (8) теңдеуге қойып -терді (8) теңдеуге қойып  өрнегін аламыз. Осы теңдеудің сол жағын топтастырсақ өрнегін аламыз. Осы теңдеудің сол жағын топтастырсақ 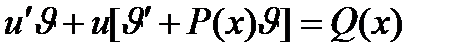 өрнегін аламыз. өрнегін аламыз. Анықталған интегралдардың қолдануы. 1) Абсциссасы [a,в] кесіндіде жататын дене берілсін. Осы дененің 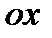 өсіне перпендикуляр әрбір қимасының ауданы өсіне перпендикуляр әрбір қимасының ауданы  белгілі болсын, онда дененің көлемі белгілі болсын, онда дененің көлемі  2) 2)  қисықпен, қисықпен,  өсімен, өсімен,  , ,  түзулермен шенелген қисықсызықты трапеция түзулермен шенелген қисықсызықты трапеция 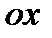 өсімен айналғанда шыққан дененің көлемі өсімен айналғанда шыққан дененің көлемі  3) 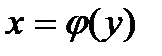 қисықпен, қисықпен,  өсімен, өсімен,  , ,  түзулермен шенелген қисықсызықты трапеция түзулермен шенелген қисықсызықты трапеция  өсімен айналғанда шыққан дененіАнықтауыштар. Анықтауыштардың қасиеттері.Анықтама. өсімен айналғанда шыққан дененіАнықтауыштар. Анықтауыштардың қасиеттері.Анықтама.  саны екінші ретті анықтауыш деп аталады да, мына түрде жазылады: саны екінші ретті анықтауыш деп аталады да, мына түрде жазылады:  Анықтауыштың қасиеттері. 1-қасиет. Анықтауыштың жолдарын сәйкес бағандармен алмастырсақ, онда оның шамасы өзгермейді.2-қасиет. Егер анықтауыштың жолдарының орнын ауыстырсақ, онда оның таңбасы өзгереді.3-қасиет. Егер анықтауыштың кейбір жолының немесе бағанының барлық элементтері нөл болса, онда анықтауыштың шамасы нөлге тең. 4-қасиет. Егер анықтауыштың кейбір жолының элементтерін k санына көбейтсек, онда анықтауыштың шамасы да осы k санына көбейтіледі. Яғни, жолының немесе бағанының ортақ көбейткішін анықтауыштың таңбасының алдына шығаруға болады. 5-қасиет.Егер анықтауыштың екі жолдарының элементтері пропорционал болса, онда анықтауыш нөлге тең.6-қасиет.Анықтауыштың қайсібір жолының элементтеріне басқа жолдың элементтерін бірдей k санына көбейтіп қосқаннан, анықтауыштың шамасы өзгермейді.7-қасиет.Егер анықтауыштың қайсібір жолы (бағаны) екі санның қосындысынан тұрса, онда бұл анықтауыш екі анықтауыштың қосындысына тең. Анықтауыштың қасиеттері. 1-қасиет. Анықтауыштың жолдарын сәйкес бағандармен алмастырсақ, онда оның шамасы өзгермейді.2-қасиет. Егер анықтауыштың жолдарының орнын ауыстырсақ, онда оның таңбасы өзгереді.3-қасиет. Егер анықтауыштың кейбір жолының немесе бағанының барлық элементтері нөл болса, онда анықтауыштың шамасы нөлге тең. 4-қасиет. Егер анықтауыштың кейбір жолының элементтерін k санына көбейтсек, онда анықтауыштың шамасы да осы k санына көбейтіледі. Яғни, жолының немесе бағанының ортақ көбейткішін анықтауыштың таңбасының алдына шығаруға болады. 5-қасиет.Егер анықтауыштың екі жолдарының элементтері пропорционал болса, онда анықтауыш нөлге тең.6-қасиет.Анықтауыштың қайсібір жолының элементтеріне басқа жолдың элементтерін бірдей k санына көбейтіп қосқаннан, анықтауыштың шамасы өзгермейді.7-қасиет.Егер анықтауыштың қайсібір жолы (бағаны) екі санның қосындысынан тұрса, онда бұл анықтауыш екі анықтауыштың қосындысына тең.
А-ң көлемі  Анықталмаған интеграл ұғымы, геометриялық мағынасы, қасиеттері.Анықталған интеграл ұғымыАнықтама. Егер (1) қосындының шегі Анықталмаған интеграл ұғымы, геометриялық мағынасы, қасиеттері.Анықталған интеграл ұғымыАнықтама. Егер (1) қосындының шегі  ұмтылғанда бар болса және ол шек [a,в] кесіндіні қалай бөлшектегенге және ұмтылғанда бар болса және ол шек [a,в] кесіндіні қалай бөлшектегенге және  нүктелерін қалай таңдап алғанға байланысты болмаса, онда ол шек нүктелерін қалай таңдап алғанға байланысты болмаса, онда ол шек  функцияның [a,в] кесіндідегі анықталған интегралы деп аталады да, мына таңбалықпен белгіленеді: функцияның [a,в] кесіндідегі анықталған интегралы деп аталады да, мына таңбалықпен белгіленеді: 
Анықталған интегралдың геометриялық мағынасы.Анықтама бойынша  анықталған интегралдың мәні анықталған интегралдың мәні  осімен, үзіліссіз осімен, үзіліссіз  функцияның графигімен және функцияның графигімен және  түзулермен шенелген қисық сызықты трапецияның ауданына тең.Анықталған интегралдың қасиеттері.1) түзулермен шенелген қисық сызықты трапецияның ауданына тең.Анықталған интегралдың қасиеттері.1)  . . 2)  . 3) . 3)  ,4) ,4)  .5) .5)  6)  ,. ,. 7)  , , 8)  9)  10)  . . 11)  , , БББББББББББББББББББББбБ Бернулли теңдеуі. Толық дифференциалдық теңдеулер.Бернулли теңдеуі.  , ,  , ,  , , 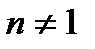
түріндегі теңдеуді Бернулли теңдеуі деп атайды. Толық дифференциалды теңдеу.  теңдеу толық дифференциалды теңдеу деп аталады. ВВВВВВВВВВВВВВВВВВВВВВВВВ Векторлар.Векторларға қолданылатын сызықтық операциялар. Қасиеттері. Векторларды базис бойынша жіктеу. Векторлардың координаттары. Векторлардың өзектігі проекциялары.Вектор деп бас нүктесi  -да соңғы нүктесi -да соңғы нүктесi  -да жататын бағытталған -да жататын бағытталған  кесiндiсiн айтады. Векторларға қолданылатын сызықтық амалдар. Векторлардың қосындысы. (Үшбұрыштар ережесі). кесiндiсiн айтады. Векторларға қолданылатын сызықтық амалдар. Векторлардың қосындысы. (Үшбұрыштар ережесі).  және және  векторлардың қосындысы деп векторлардың қосындысы деп  вектордың басы мен вектордың басы мен  вектордың соңғы нүктесiн қосатын вектордың соңғы нүктесiн қосатын  векторын айтады.Екi векторын айтады.Екi  және және  векторлардың айырымы деп векторлардың айырымы деп  және және  векторлардың қосындысы болатын векторлардың қосындысы болатын  векторын айтады. векторын айтады.  вектордың нақты вектордың нақты  санға көбейтiндiсi деп ұзындығы санға көбейтiндiсi деп ұзындығы 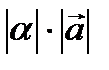 тең, тең,  векторына коллинеарлы, егер векторына коллинеарлы, егер  болса, онда болса, онда  векторына бағыттас, егер векторына бағыттас, егер  онда онда  векторына қарама-қарсы бағыттас векторына қарама-қарсы бағыттас  векторын айтады. Векторларға қолданылатын сызықтық амалдардың қасиеттері: векторын айтады. Векторларға қолданылатын сызықтық амалдардың қасиеттері: 1)  2) 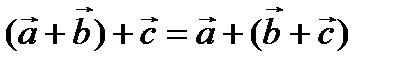 3) 3)  4)  5) 5) 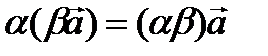 6) 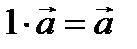 7) 7)  8)    Векторлардың проекциялары.Анықтама: Векторлардың проекциялары.Анықтама:  вектордың вектордың  түзуіндегі сандық проекциясы деп, түзуіндегі сандық проекциясы деп,  вектордың ұзындығының вектордың ұзындығының  векторы мен векторы мен  түзудің арасындағы түзудің арасындағы  бұрышының косинусына көбейтіндісін айтады, яғни бұрышының косинусына көбейтіндісін айтады, яғни  Векторладың скалярлық, вееторлық ж/е аралас көбейтінділері. Қасиеттері. Қолданулары. 
Скалярлық көбейтіндінің қасиеттері:  

  Векторлық көбейтiндiнiң кейбiр қасиеттерi:1-қасиет. Векторлық көбейтiндiнiң кейбiр қасиеттерi:1-қасиет.  вектордың ұзындығы, бас нүктелерi бiр нүктеге орналасқан вектордың ұзындығы, бас нүктелерi бiр нүктеге орналасқан  мен мен 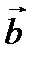 векторларынан құрылған параллелограммның ауданына тең. 2-қасиет. Векторлық көбейтiндi нөлге тең, егер векторларынан құрылған параллелограммның ауданына тең. 2-қасиет. Векторлық көбейтiндi нөлге тең, егер  мен мен 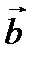 векторлары коллинеарлы болса немесе екеуiнiң бiреуi нөлдiк вектор болса. 3-қасиет. векторлары коллинеарлы болса немесе екеуiнiң бiреуi нөлдiк вектор болса. 3-қасиет.  4-қасиет. 4-қасиет.    5-қасиет.Егер 5-қасиет.Егер  және және  векторлардың координаттары берілсе, онда олардың векторлық көбейтіндісін былай жазуға болады: векторлардың координаттары берілсе, онда олардың векторлық көбейтіндісін былай жазуға болады:  . Онда . Онда  және және  векторлардан құрылған параллелограммның ауданы векторлардан құрылған параллелограммның ауданы  . .  және және  векторлардан құрылған үшбұрыштың ауданы векторлардан құрылған үшбұрыштың ауданы
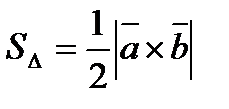 . .
Аралас көбейтіндінің қасиеттері:1-қасиет.  аралас көбейтінді аралас көбейтінді 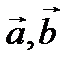 және және 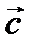 векторларынан құрылған бағытталған параллелепипедтің көлеміне тең. 2-қасиет. Егер векторларынан құрылған бағытталған параллелепипедтің көлеміне тең. 2-қасиет. Егер  векторлары компланарлы болса, онда аралас көбейтінді нөлге тең.3-қасиет. Егер аралас көбейтіндінiң көбейткіштерiн циклдiк орын алмастырсақ оның мәнi өзгермейді векторлары компланарлы болса, онда аралас көбейтінді нөлге тең.3-қасиет. Егер аралас көбейтіндінiң көбейткіштерiн циклдiк орын алмастырсақ оның мәнi өзгермейді  4-қасиет.Аралас көбейтіндінің сызықтық қасиеті.  ДДДДДДДДДДДДДДДДДДДДДДДДД Дирихле қатары. Таңба ауыспалы қатар. Лейбниц белгісі.Ауыспа таңбалы қатардың  (4) (4)
Мүшелері бірсарынды кемімелі болсын, яғни 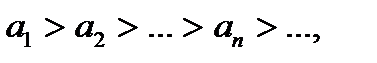 сонымен бірге сонымен бірге  (5) (5)
болсын. (5) шартты Лейбниц белгісі деп атайды.  Дирихле қатарын жинақтылыққа зерттеу керек. Дирихле қатарын жинақтылыққа зерттеу керек.
Шешімі: , ,  , ,  . 1) . 1) 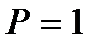 болса, болса,  . . 3)  болса болса  . . Сонымен  болса, Дирихле қатары жинақты, ал болса, Дирихле қатары жинақты, ал  үшін Дирихле қатары жинақсыз. үшін Дирихле қатары жинақсыз. Дәрежелік қатарлар ұғымы. Дәрежелік қатарлардың жинақтылық радиусы ж/е интервалы. Тейлор ж/е Маклорен қатарлары.  −ің дәрежелерінен тұратын −ің дәрежелерінен тұратын  функциялық қатарларды дәрежелі қатарлар деп атайды. Дәрежелі қатардың жинақтылық интервалындағы функциялық қатарларды дәрежелі қатарлар деп атайды. Дәрежелі қатардың жинақтылық интервалындағы  , ,  ең үлкен мәні дәрежелі қатардың жинақтылық радиусы деп аталады да ең үлкен мәні дәрежелі қатардың жинақтылық радиусы деп аталады да  әрпімен белгіленеді, яғни әрпімен белгіленеді, яғни  . Егер қатар тек . Егер қатар тек  нүктеде жинақталса, онда нүктеде жинақталса, онда  , егер (3) қатар барлық , егер (3) қатар барлық 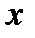 нүктесінде жинақталса, онда нүктесінде жинақталса, онда  . (3) қатардың жинақтылық радиустерін Даламбер және Коши белгілері арқылы табуға болады . (3) қатардың жинақтылық радиустерін Даламбер және Коши белгілері арқылы табуға болады  (4) (4)  (5) Егер (5) Егер  функцияның функцияның  нүктенің маңында кез келген ретті туындылары бар болса, онда оны осы нүкте маңында Тейлор қатарына жіктеуге болады нүктенің маңында кез келген ретті туындылары бар болса, онда оны осы нүкте маңында Тейлор қатарына жіктеуге болады
 Егер Егер  болса, онда болса, онда  (7) (7)
(7) қатарды Маклорен қатары деп атайды. sinx,cosx элементар функцияларын Маклорен қатарына жіктеу.
 




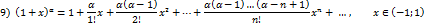
Дәрежелі қатарлардың қолданылуы.  −ің дәрежелерінен тұратын −ің дәрежелерінен тұратын  (3) немесе (3) немесе 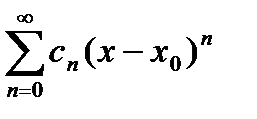 (4) функциялық қатарларды дәрежелі қатарлар деп атайды. Мұндағы (4) функциялық қатарларды дәрежелі қатарлар деп атайды. Мұндағы  , ,  сандары дәрежелі қатардың коэффициенттері деп аталады. (1)−қатардағы сандары дәрежелі қатардың коэффициенттері деп аталады. (1)−қатардағы  немесе немесе  , ,  −тұрақты сан.Дәрежелі қатарлар арқылы анықталған интегралдарды берілген дәлдікпен есептеуге болады. Дәрежелі қатарлардың көмегімен дифференциалдық теңдеулерді жуықтап есептеуге болады. −тұрақты сан.Дәрежелі қатарлар арқылы анықталған интегралдарды берілген дәлдікпен есептеуге болады. Дәрежелі қатарлардың көмегімен дифференциалдық теңдеулерді жуықтап есептеуге болады.
Дифференциалдық теңдеулердің негізгі ұғымы ж/е анықтамалары. Айнымалылары ажыратылған ж/е ажыратылатын бірінші ретті дифференциалдық теңдеулер.  ретті дифференциалдық теңдеудің (ДТ) жалпы түрі ретті дифференциалдық теңдеудің (ДТ) жалпы түрі  (1) (1)
Мұндағы  −тәуелсіз айнымалы, −тәуелсіз айнымалы,  −белгісіз функция, −белгісіз функция, 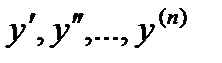 оның туындылары. (1) теңдеудегі туындының ең жоғарғы реті ДТ реті деп аталады. Егер оның туындылары. (1) теңдеудегі туындының ең жоғарғы реті ДТ реті деп аталады. Егер  болса, онда болса, онда  (2) (2)
(2) теңдеу бірінші ретті ДТ деп аталады. Айнымалылары ажыратылған және ажыратылатын бірінші ретті ДТ−лер. а)  түрдегі ДТ айнымалылары ажыратылған теңдеу деп аталады. Оның жалпы интегралы  б)  түрдегі теңдеу айнымалылары ажыратылатын теңдеу деп аталады. Бұл теңдеудің жалпы интегралы мынаған тең: түрдегі теңдеу айнымалылары ажыратылатын теңдеу деп аталады. Бұл теңдеудің жалпы интегралы мынаған тең: Дискретті кездейсоқ шамалар ж/е олардың үлестірім заңдары.Кездейсоқ шама дегеніміз – сандық мән қабылдайтын, бірақ қандай мәнді қабылдайтының алдын – ала айтуға болмайтын шамалар. Анықтама.  кездейсоқ шамасының қабылдайтын мәндері ақырлы бүтін сандар немесе тізбек түрінде жазылса, онда кездейсоқ шамасының қабылдайтын мәндері ақырлы бүтін сандар немесе тізбек түрінде жазылса, онда  кездейсоқ шамасын дискретті деп атайды. ДКШ – нің жиі кездесетін үлестірім заңдары: кездейсоқ шамасын дискретті деп атайды. ДКШ – нің жиі кездесетін үлестірім заңдары: 1) Биномды үлестірім  , ,  . . 2)Пуассон үлестірімі  , ,  , ,  3)Геометриялық үлестірім  , ,  4)Гипергеометриялық үлестірім  , ,  , ,  . .
Дисперсия ж/е оның қасиеттері. Орташа квадраттық ауытқу. Мода. Медиа. Анықтама.  кездейсоқ шамасының дисперсиясы деп кездейсоқ шаманың математикалық күтімінен ауытқуының квадратының математикалық күтімін айтады, яғни кездейсоқ шамасының дисперсиясы деп кездейсоқ шаманың математикалық күтімінен ауытқуының квадратының математикалық күтімін айтады, яғни   а) Дискретті кездейсоқ шама үшін 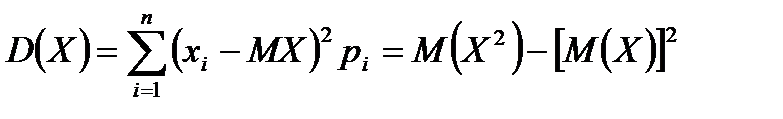 б) Үзіліссіз кездейсоқ шама үшін б) Үзіліссіз кездейсоқ шама үшін    Дисперсияның қасиеттері: 1)  2`) 2`)  3)  , мұндағы , мұндағы  және және  тәуелсіз кездейсоқ шамалар. тәуелсіз кездейсоқ шамалар. 4)  , ,  Анықтама. Анықтама. шамасынорташа квадраттық ауытқудеп атайды. Анықтама. шамасынорташа квадраттық ауытқудеп атайды. Анықтама. дискреттікездейсоқ шамасының модасы дискреттікездейсоқ шамасының модасы  деп, оның ең ықтималды болатын мәнін айтады, ал үзіліссіз кездейсоқ шама үшін- деп, оның ең ықтималды болатын мәнін айтады, ал үзіліссіз кездейсоқ шама үшін-  - ның максимум болатын нүктесі. Егер - ның максимум болатын нүктесі. Егер  - ның бірнеше локальды максимумы болса, онда - ның бірнеше локальды максимумы болса, онда  - ың сонша модасы болады. Анықтама.Үзіліссіз кездейсоқ шаманың медианасы - ың сонша модасы болады. Анықтама.Үзіліссіз кездейсоқ шаманың медианасы  деп оның деп оның  < <  > >  , болатын , болатын  мәнін айтады. мәнін айтады. ЖЖЖЖЖЖЖЖЖЖЖЖЖЖЖ Жазықтықтағы түзудің теңдеулері. Жазықтықтағы түзудің векторлық түріндегі теңдеуі   Жазықтықтағы түзудiң нормаль түріндегі теңдеу Жазықтықтағы түзудiң нормаль түріндегі теңдеу 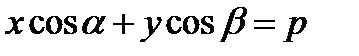  Жазықтықтағы түзудің жалпы түрдегі теңдеуі 
Жазықтықтағы түзудің кесіндідегі теңдеуі 
Жазықтықта жатқан екі  және және  түзулері берілсін түзулері берілсін 

Екі түзудің арасындағы бұрыш 
Жоғарғы шегі айнымалы интегралдар. Ньютон-Лейбниц формуласы. Анықталған интегралдарды. Есептеу әдістері. Жұп ж/е тақ функцияларды интегралдау.  (5) формуланы Ньютон-Лейбниц формуласы дейді. Анықталған интегралдарды есептеу әдістері. (5) формуланы Ньютон-Лейбниц формуласы дейді. Анықталған интегралдарды есептеу әдістері. а)Бөліктеп интегралдау әдісі.  б) Айнымалыны ауыстыру әдісі(алмастыру әдісі). 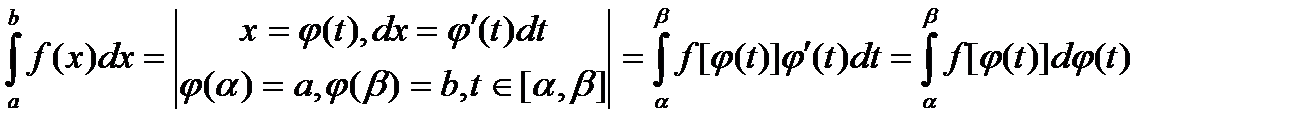 Жұп және тақ функцияларды интегралдау. Теорема. Жұп және тақ функцияларды интегралдау. Теорема.  функциясы [a,в]-да интегралдансын. Онда функциясы [a,в]-да интегралдансын. Онда
1)егерде  -жұп болса, онда -жұп болса, онда  2) егерде  -тақ болса, онда -тақ болса, онда  Жоғарғы ретті дифференциалдық теңдеулер. Реті төмендетілетін жоғарғы ретті дифференциалдық теңдеулер. Жоғарғы ретті дифференциалдық теңдеулер. Реті төмендетілетін жоғарғы ретті дифференциалдық теңдеулер.  -ретті ДТ-ің жалпы түрі -ретті ДТ-ің жалпы түрі  
Реті төмендетілетін дифференциалдық теңдеулер а)  түріндегі теңдеулерді қарастырайық. түріндегі теңдеулерді қарастырайық.  екендігін ескеріп теңдеудің екі жағын екендігін ескеріп теңдеудің екі жағын 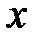 бойынша интегралдап бойынша интегралдап 

Жоғарғы ретті сызықты дифференциалдық теңдеулер. Функциалардың сызықтың тәуелсіздігі. Вронский анықтауышы. Біртекті ж/е біртексіз сызықтық дифференциалдық теңдеулердің жалпы шешімдері.  -ші ретті біртексіз сызықты ДТ-дің жалпы түрі -ші ретті біртексіз сызықты ДТ-дің жалпы түрі   теңдеуі теңдеуі  -ші ретті біртекті сызықты ДТ деп аталады.Анықтама. -ші ретті біртекті сызықты ДТ деп аталады.Анықтама.  интервалында интервалында  функцияларын сызықты тәуелді дейміз. функцияларын сызықты тәуелді дейміз.  (8) Егер (8) теңдік тек (8) Егер (8) теңдік тек  үшін ғана орындалса, онда үшін ғана орындалса, онда  функцияларын сызықты тәуелсіз дейміз. функцияларын сызықты тәуелсіз дейміз.


өрнегін Вронскийдің анықтауышы деп атайды.Теорема.Біртексіз сызықты дифференциалдық теңдеудің  жалпы шешімі оның жалпы шешімі оның  дербес шешімі мен оған сәйкес дербес шешімі мен оған сәйкес  біртекті теңдеудің біртекті теңдеудің  жалпы шешімінің қосындысына тең, яғни жалпы шешімінің қосындысына тең, яғни  . . .Жиліктің анықмасы. Ықтималдықтың статистикалық, классикалық, геометриялық анықтамалары.Жиіліктің анықтамасы.  оқиғасының жиілігі деп оқиғасының жиілігі деп оқиға пайда болған тәжірибе санының барлық тәжірибе санына қатынасын айтады. Жиілікті оқиға пайда болған тәжірибе санының барлық тәжірибе санына қатынасын айтады. Жиілікті  деп белгілесек, онда деп белгілесек, онда  . . Ықтималдықтың статистикалық анықтамасы.Тәжірибе санын көбейткенде кездейсоқ оқиғаның жиілігінің ұмтылатын тұрақты санды осы оқиғаның ықтималдығы деп атайды. Ықтималдықтың классикалық анықтамасы.  -элементар оқиғалар кеңістігі, -элементар оқиғалар кеңістігі,  - шектелген. Әрбір элементар - шектелген. Әрбір элементар  оқиғасына оқиғасына  санын сәйкес қойып, мұндай жағдай да элементар оқиғаларды тең мүмкіндікті,ал санын сәйкес қойып, мұндай жағдай да элементар оқиғаларды тең мүмкіндікті,ал оқиғасына енетінэлементар оқиғаларды оқиғасына енетінэлементар оқиғаларды  -ға қолайлы деп атайды. Геометриялық ықтималдық. Егер -ға қолайлы деп атайды. Геометриялық ықтималдық. Егер  және және  аймақтарының өлшемдері аймақтарының өлшемдері  және және  бар болса, лақтырылған нүктенің бар болса, лақтырылған нүктенің  аймағына түсу ықтималдығы аймағына түсу ықтималдығы  теңдігімен анықталады. теңдігімен анықталады.  санын геометриялық ықтималдық деп атайды. Егер кесіндіні қарастырсақ, санын геометриялық ықтималдық деп атайды. Егер кесіндіні қарастырсақ,  , ,  - ұзындықтар, ал жазықтықта аудандар, кеңістікте - ұзындықтар, ал жазықтықта аудандар, кеңістікте  , ,  - көлемдер. - көлемдер.
ЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕ Екінші ретті қисықтың теңдеулері.Екінші ретті қисықтардың жалпы теңдеуі 
1.Шеңбер.  шеңбердiң канондық теңдеуi. шеңбердiң канондық теңдеуi. 2.Эллипс.   эллипстiң канондық теңдеуi. эллипстiң канондық теңдеуi.
3. Гипербола. Гиперболаның канондық теңдеуi  
4. Парабола.Параболаның канондық теңдеуi  
ККККККККК---ҚҚҚҚҚҚҚҚҚҚҚҚҚ .Комплекс сандар. Комплекс санның алгебралық формасы. Комплекс санға аламдар қолдану.Анықтама. Кез келген  нақты сандар қосағын комплекс сандар деп атайды. егер олар үшін теңдік және қосу мен көбейту амалдар ұғымы былай анықталса:1Екі нақты сандар қосағын комплекс сандар деп атайды. егер олар үшін теңдік және қосу мен көбейту амалдар ұғымы былай анықталса:1Екі  және және  комплекс сандарды бір бірімен тең дейміз, тек сонда ғана, егер комплекс сандарды бір бірімен тең дейміз, тек сонда ғана, егер  болса; 2Екі болса; 2Екі  және және  комплекс сандардың қосындысы деп комплекс сандардың қосындысы деп  комплекс санын айтады.3Екі комплекс санын айтады.3Екі  және және  комплекс сандарының көбейтіндісі деп комплекс сандарының көбейтіндісі деп  комплекс санын айтады. комплекс санын айтады.  түрдегі комплекс сандарды алгебралық формадағы комплекс сан деп атайды.Енді теңдікті, қосу мен көбейту амалдарды былай жазуға болады. түрдегі комплекс сандарды алгебралық формадағы комплекс сан деп атайды.Енді теңдікті, қосу мен көбейту амалдарды былай жазуға болады.     комплекс санды комплекс санды  комплекс санның түйіндесі деп атайды. комплекс санның түйіндесі деп атайды. .Комплекс санның тригонометриялық ж/е көрсеткіштік формалары. Модуль ж/е аргумент. Эйлер формуласы. Муавр формуласы. Түйндес комплекс сандардың қасиеттері.  - түрдегі комплекс санды тригонометриялық формадағы комплекс сан деп атайды. - түрдегі комплекс санды тригонометриялық формадағы комплекс сан деп атайды.  -комплекс санының аргументі, -комплекс санының аргументі, 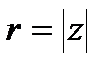 комплекс санының модулі. комплекс санының модулі.    түрдегі комплекс санды көрсеткіштік формадағы комплекс сан деп атайды. Екі комплекс санды көбейткенде олардың модульдері көбейтіледі де, аргументтері қосылады, яғни түрдегі комплекс санды көрсеткіштік формадағы комплекс сан деп атайды. Екі комплекс санды көбейткенде олардың модульдері көбейтіледі де, аргументтері қосылады, яғни 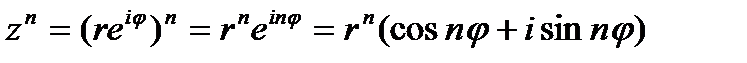 -формула Муаврдың формуласы деп аталады. -формула Муаврдың формуласы деп аталады.
 Эйлер формулалары деп Крамер ережесі. Гаусс әдісі. Кері матрица әдісі. Эйлер формулалары деп Крамер ережесі. Гаусс әдісі. Кері матрица әдісі.  белгiсiздерi бар белгiсiздерi бар  теңдеулер жүйесiн қарастырайық теңдеулер жүйесiн қарастырайық  (5) Осы жүйенiң негiзгi матрицасының анықтауышы (5) Осы жүйенiң негiзгi матрицасының анықтауышы  . Бұл жағдайда . Бұл жағдайда  кері матрица бар болады. (5) теңдіктің екі жағын сол жақтан кері матрица бар болады. (5) теңдіктің екі жағын сол жақтан  матрицаға көбейтіп мынаны аламыз: матрицаға көбейтіп мынаны аламыз:    (6) (6)
(6) формуланы (5) теңдеудің кері матрица әдісімен алынған шешімі деп аталады. (6) теңдiктi былай ашып жазсақ: 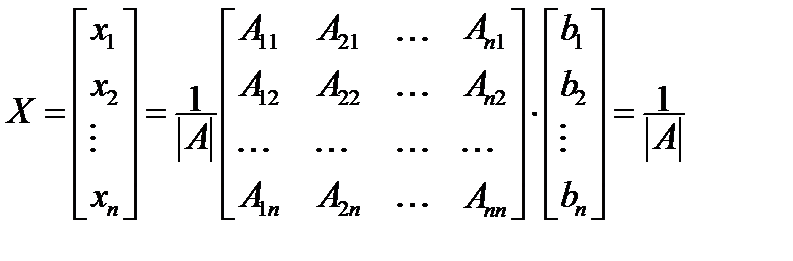 
 (8) (8) өрнектерi Крамер формулалары деп аталады. (8) (8) өрнектерi Крамер формулалары деп аталады.
Гаусс әдiсi сызықты теңдеулер жүйесiн шешудегi универсалды әдiстердiң бiрi деп есептелiнедi. Бұл әдiс кейде айнымалыларды бiртiндеп жою әдiсi деп те аталынады.  Кеңестіктегі түзудің ж/е жазықтықтың теңдеулері. Кеңестіктегі түзудің ж/е жазықтықтың теңдеулері.
Жазықтықтың нормаль түріндегі теңдеуі   (2) (2)
Жазықтықтың жалпы түрдегі теңдеуі  , , 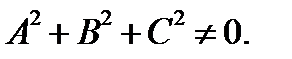 (3) (3)
 векторы жазықтықтың нормалі деп аталады. векторы жазықтықтың нормалі деп аталады.
Жазықтықтың кесіндідегі теңдеуі  (4) (4)
Кеңістіктегі түзудің теңдеулерінің түрлері.  (11) (11)
(11) теңдеулердi түзудiң канондық теңдеулерi деп атайды.  (12) түзудің параметрлі түріндегі теңдеулері. (12) түзудің параметрлі түріндегі теңдеулері.
 осы (14) түзудің кеңістіктегі жалпы түрдегi теңдеулерi деп атайды. осы (14) түзудің кеңістіктегі жалпы түрдегi теңдеулерi деп атайды.
Коэффициеннтері тұрақты сызықты жоғарғы ретті біртекті дифференциалдық теңдеулер.  мұндағы 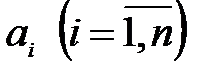 тұрақты сандар, коэффициенттері тұрақты сызықты біртекті ДТдеп аталады. ДТ-дің сипаттауыш теңдеуін аламыз: тұрақты сандар, коэффициенттері тұрақты сызықты біртекті ДТдеп аталады. ДТ-дің сипаттауыш теңдеуін аламыз:  (11) Егер (11) Егер  (11) теңдеудің түбірі болса, онда (11) теңдеудің түбірі болса, онда  (10) теңдеудің дербес шешімі болады және керісінше.а) Егер (11) теңдеудің түбірлері (10) теңдеудің дербес шешімі болады және керісінше.а) Егер (11) теңдеудің түбірлері  әртүрлі нақты сандар болса, онда әртүрлі нақты сандар болса, онда  функциялары (10) теңдеудің функциялары (10) теңдеудің  сызықты тәуелсіз шешімі болады.Онда (10) теңдеудің жалпы шешімі сызықты тәуелсіз шешімі болады.Онда (10) теңдеудің жалпы шешімі

Коэффициеннтері тұрақты сызықты жоғарғы ретті біртексіз дифференциалдық теңдеулер.  (13)Бұл теңдеудің жалпы шешімі (13)Бұл теңдеудің жалпы шешімі  болады, мұндағы болады, мұндағы  - (13) теңдеудің дербес шешімі, ал - (13) теңдеудің дербес шешімі, ал  функциялар функциялар  біртекті (10) теңдеудің іргелі жүйе шешімдері. Бұл шешімдерді табу әдісі жоғарыда көрсетілген. (13) теңдеудің оң жағы біртекті (10) теңдеудің іргелі жүйе шешімдері. Бұл шешімдерді табу әдісі жоғарыда көрсетілген. (13) теңдеудің оң жағы  ( 14) ( 14)
болсын, мұндағы  және және   -ші және -ші және  -ші дәрежелі коэффициенттері тұрақты көпмүшеліктер. (14) өрнектің дербес жағдайларын қарастырайық. -ші дәрежелі коэффициенттері тұрақты көпмүшеліктер. (14) өрнектің дербес жағдайларын қарастырайық. 1)  болсын. болсын. а)  саны сипаттауыш теңдеудің түбірі болмасын. Онда (13) теңдеудің дербес шешімін саны сипаттауыш теңдеудің түбірі болмасын. Онда (13) теңдеудің дербес шешімін  түрде іздейміз. Мұндағы түрде іздейміз. Мұндағы  -дер белгісіз тұрақты коэффициенттер. Бұл (16) шешімді (13) теңдеуге қойып теңдіктің екі жағындағы бірдей дәрежелі -дер белгісіз тұрақты коэффициенттер. Бұл (16) шешімді (13) теңдеуге қойып теңдіктің екі жағындағы бірдей дәрежелі 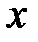 -тің алдындағы коэффициенттерін теңестіріп белгісіз -тің алдындағы коэффициенттерін теңестіріп белгісіз 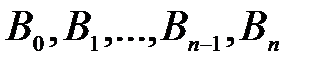 үшін үшін  алгебралық теңдеулер жүйесін аламыз. Осы жүйеден белгісіз коэффициенттерді табамыз. алгебралық теңдеулер жүйесін аламыз. Осы жүйеден белгісіз коэффициенттерді табамыз. б)  саны сипаттауыш теңдеудің саны сипаттауыш теңдеудің 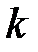 еселі түбірі болсын, онда (13) теңдеудің дербес шешімін еселі түбірі болсын, онда (13) теңдеудің дербес шешімін 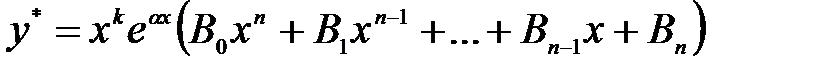 түрінде іздейміз. түрінде іздейміз.
Кездейсоқ оқиғалардың анықтамалары. Оқиғаларға қолданылатын амалдар.Анықтама 1. Ықтималдықтар теориясында оқиғадеп қайсыбыр тәжірибе нәтижесінде пайда болатын әрбір фактыны айтады.Анықтама 2.Егер барлық тәжірибеде қарастырылып отырғаноқиға әрқашанда пайда болса, ондай оқиғаны ақиқат оқиға дейді. Анықтама 3.Егер барлық тәжірибеде қарастырылып отырғаноқиға ешқашанда пайда болмаса, ондай оқиғаны мүмкін емес оқиға деп атайды. Анықтама 4.
| 



 саны екінші ретті анықтауыш деп аталады да, мына түрде жазылады:
саны екінші ретті анықтауыш деп аталады да, мына түрде жазылады:
 белгiсiздерi бар
белгiсiздерi бар 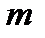 теңдеулерден тұратын сызықты жүйе деп, мынандай теңдеулер жүйесiн айтады ( 1)
теңдеулерден тұратын сызықты жүйе деп, мынандай теңдеулер жүйесiн айтады ( 1) 
 теңдеулер жүйесiнiң коэффициенттерi,
теңдеулер жүйесiнiң коэффициенттерi, 
 жүйенiң бос мүшелерi, Ең кемiнде бiр шешiмi бар теңдеулер жүйесiн үйлесiмдi,ал шешiмi жоқ теңдеулер жүйесiн үйлесiмсiздеп атайды. Тек қана бiр ғана шешiмi бар жүйенi анықталған, ал бiрден артық шешiмi бар жүйенi анықталмаған деп атайды. Егер барлық
жүйенiң бос мүшелерi, Ең кемiнде бiр шешiмi бар теңдеулер жүйесiн үйлесiмдi,ал шешiмi жоқ теңдеулер жүйесiн үйлесiмсiздеп атайды. Тек қана бiр ғана шешiмi бар жүйенi анықталған, ал бiрден артық шешiмi бар жүйенi анықталмаған деп атайды. Егер барлық  болса, онда (1) жүйе бiртектi, ал ең болмағанда бос мүшелердiң бiреуi нөлге тең болмаса ол бiртектi емес деп аталады.
болса, онда (1) жүйе бiртектi, ал ең болмағанда бос мүшелердiң бiреуi нөлге тең болмаса ол бiртектi емес деп аталады. функцияның алғашқы функцияларының
функцияның алғашқы функцияларының  жиынын
жиынын  символымен белгілейді. Анықталмаған интегралдың қасиеттері.
символымен белгілейді. Анықталмаған интегралдың қасиеттері. ,
, 
 1
1 ,
, 
 функциясы
функциясы  ,
, .
. , Айнымалылары бойынша біртекті дифференциалдық теңдеулер. Бірінші ретті сызықтық дифференциалдық теңдеулер.
, Айнымалылары бойынша біртекті дифференциалдық теңдеулер. Бірінші ретті сызықтық дифференциалдық теңдеулер.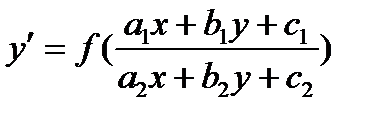 теңдеуін біртекті теңдеуге келтіру үшін
теңдеуін біртекті теңдеуге келтіру үшін  ,
,  деп алып жаңа
деп алып жаңа  және
және  айнымалыларын енгізу керек, мұндағы
айнымалыларын енгізу керек, мұндағы 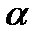 және
және  белгісіз сандарды берілген теңдеу біртекті болатындай етіп табу керек. Яғни олар
белгісіз сандарды берілген теңдеу біртекті болатындай етіп табу керек. Яғни олар 
 фкнкция мен оның туындысы
фкнкция мен оның туындысы  сызықты болатын теңдеуді айтады.
сызықты болатын теңдеуді айтады. (8)
(8) және
және 
 кесіндідегі үзіліссіз функциялар. Егер
кесіндідегі үзіліссіз функциялар. Егер  аралығында
аралығында  болмаса, онда (8) теңдеуді біртексіз ал
болмаса, онда (8) теңдеуді біртексіз ал  болса біртекті сызықты теңдеу деп аталады.
болса біртекті сызықты теңдеу деп аталады. біртекті теңдеудің жалпы шешімі
біртекті теңдеудің жалпы шешімі  , мұндағы с-кез келген тұрақты сан. Тұрақтыны вариациалау әдісі бойынша (8) теңдеудің жалпы шешімін
, мұндағы с-кез келген тұрақты сан. Тұрақтыны вариациалау әдісі бойынша (8) теңдеудің жалпы шешімін  түрінде іздейді.
түрінде іздейді.
 , онда
, онда  .
.  және
және  -терді (8) теңдеуге қойып
-терді (8) теңдеуге қойып  өрнегін аламыз. Осы теңдеудің сол жағын топтастырсақ
өрнегін аламыз. Осы теңдеудің сол жағын топтастырсақ 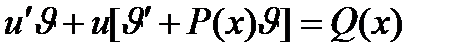 өрнегін аламыз.
өрнегін аламыз.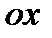 өсіне перпендикуляр әрбір қимасының ауданы
өсіне перпендикуляр әрбір қимасының ауданы  белгілі болсын, онда дененің көлемі
белгілі болсын, онда дененің көлемі  2)
2)  қисықпен,
қисықпен,  өсімен,
өсімен,  ,
,  түзулермен шенелген қисықсызықты трапеция
түзулермен шенелген қисықсызықты трапеция 
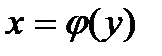 қисықпен,
қисықпен,  өсімен,
өсімен,  ,
,  түзулермен шенелген қисықсызықты трапеция
түзулермен шенелген қисықсызықты трапеция  Анықталмаған интеграл ұғымы, геометриялық мағынасы, қасиеттері.Анықталған интеграл ұғымыАнықтама. Егер (1) қосындының шегі
Анықталмаған интеграл ұғымы, геометриялық мағынасы, қасиеттері.Анықталған интеграл ұғымыАнықтама. Егер (1) қосындының шегі  ұмтылғанда бар болса және ол шек [a,в] кесіндіні қалай бөлшектегенге және
ұмтылғанда бар болса және ол шек [a,в] кесіндіні қалай бөлшектегенге және  нүктелерін қалай таңдап алғанға байланысты болмаса, онда ол шек
нүктелерін қалай таңдап алғанға байланысты болмаса, онда ол шек  функцияның [a,в] кесіндідегі анықталған интегралы деп аталады да, мына таңбалықпен белгіленеді:
функцияның [a,в] кесіндідегі анықталған интегралы деп аталады да, мына таңбалықпен белгіленеді:
 анықталған интегралдың мәні
анықталған интегралдың мәні  осімен, үзіліссіз
осімен, үзіліссіз  функцияның графигімен және
функцияның графигімен және  түзулермен шенелген қисық сызықты трапецияның ауданына тең.Анықталған интегралдың қасиеттері.1)
түзулермен шенелген қисық сызықты трапецияның ауданына тең.Анықталған интегралдың қасиеттері.1)  .
. . 3)
. 3)  ,4)
,4)  .5)
.5) 
 ,.
,. ,
,

 .
. ,
, ,
,  ,
,  ,
, 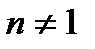

 -да соңғы нүктесi
-да соңғы нүктесi  -да жататын бағытталған
-да жататын бағытталған  кесiндiсiн айтады. Векторларға қолданылатын сызықтық амалдар. Векторлардың қосындысы. (Үшбұрыштар ережесі).
кесiндiсiн айтады. Векторларға қолданылатын сызықтық амалдар. Векторлардың қосындысы. (Үшбұрыштар ережесі).  және
және  векторлардың қосындысы деп
векторлардың қосындысы деп  векторын айтады.Екi
векторын айтады.Екi  векторлардың айырымы деп
векторлардың айырымы деп  векторлардың қосындысы болатын
векторлардың қосындысы болатын  векторын айтады.
векторын айтады.  санға көбейтiндiсi деп ұзындығы
санға көбейтiндiсi деп ұзындығы 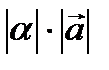 тең,
тең,  болса, онда
болса, онда  онда
онда  векторына қарама-қарсы бағыттас
векторына қарама-қарсы бағыттас  векторын айтады. Векторларға қолданылатын сызықтық амалдардың қасиеттері:
векторын айтады. Векторларға қолданылатын сызықтық амалдардың қасиеттері:
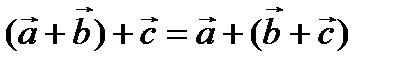 3)
3) 
 5)
5) 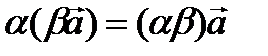
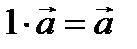 7)
7) 


 Векторлардың проекциялары.Анықтама:
Векторлардың проекциялары.Анықтама:  вектордың
вектордың  түзуіндегі сандық проекциясы деп,
түзуіндегі сандық проекциясы деп,  векторы мен
векторы мен  бұрышының косинусына көбейтіндісін айтады, яғни
бұрышының косинусына көбейтіндісін айтады, яғни 





 Векторлық көбейтiндiнiң кейбiр қасиеттерi:1-қасиет.
Векторлық көбейтiндiнiң кейбiр қасиеттерi:1-қасиет.  вектордың ұзындығы, бас нүктелерi бiр нүктеге орналасқан
вектордың ұзындығы, бас нүктелерi бiр нүктеге орналасқан  мен
мен  векторларынан құрылған параллелограммның ауданына тең. 2-қасиет. Векторлық көбейтiндi нөлге тең, егер
векторларынан құрылған параллелограммның ауданына тең. 2-қасиет. Векторлық көбейтiндi нөлге тең, егер  мен
мен  4-қасиет.
4-қасиет. 

 5-қасиет.Егер
5-қасиет.Егер  және
және  векторлардың координаттары берілсе, онда олардың векторлық көбейтіндісін былай жазуға болады:
векторлардың координаттары берілсе, онда олардың векторлық көбейтіндісін былай жазуға болады:  . Онда
. Онда  және
және  векторлардан құрылған параллелограммның ауданы
векторлардан құрылған параллелограммның ауданы  .
. 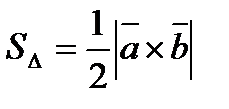 .
. аралас көбейтінді
аралас көбейтінді 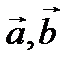 және
және 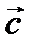 векторларынан құрылған бағытталған параллелепипедтің көлеміне тең. 2-қасиет. Егер
векторларынан құрылған бағытталған параллелепипедтің көлеміне тең. 2-қасиет. Егер  векторлары компланарлы болса, онда аралас көбейтінді нөлге тең.3-қасиет. Егер аралас көбейтіндінiң көбейткіштерiн циклдiк орын алмастырсақ оның мәнi өзгермейді
векторлары компланарлы болса, онда аралас көбейтінді нөлге тең.3-қасиет. Егер аралас көбейтіндінiң көбейткіштерiн циклдiк орын алмастырсақ оның мәнi өзгермейді 

 (4)
(4)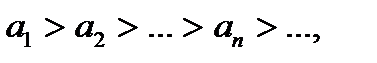 сонымен бірге
сонымен бірге (5)
(5) Дирихле қатарын жинақтылыққа зерттеу керек.
Дирихле қатарын жинақтылыққа зерттеу керек. ,
,  ,
,  . 1)
. 1) 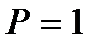 болса,
болса,  .
. болса
болса  .
. үшін Дирихле қатары жинақсыз.
үшін Дирихле қатары жинақсыз. −ің дәрежелерінен тұратын
−ің дәрежелерінен тұратын  функциялық қатарларды дәрежелі қатарлар деп атайды. Дәрежелі қатардың жинақтылық интервалындағы
функциялық қатарларды дәрежелі қатарлар деп атайды. Дәрежелі қатардың жинақтылық интервалындағы  ,
,  ең үлкен мәні дәрежелі қатардың жинақтылық радиусы деп аталады да
ең үлкен мәні дәрежелі қатардың жинақтылық радиусы деп аталады да  әрпімен белгіленеді, яғни
әрпімен белгіленеді, яғни  . Егер қатар тек
. Егер қатар тек  нүктеде жинақталса, онда
нүктеде жинақталса, онда  , егер (3) қатар барлық
, егер (3) қатар барлық 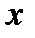 нүктесінде жинақталса, онда
нүктесінде жинақталса, онда  . (3) қатардың жинақтылық радиустерін Даламбер және Коши белгілері арқылы табуға болады
. (3) қатардың жинақтылық радиустерін Даламбер және Коши белгілері арқылы табуға болады  (4)
(4)  (5) Егер
(5) Егер  функцияның
функцияның  Егер
Егер  (7)
(7)





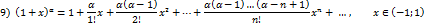
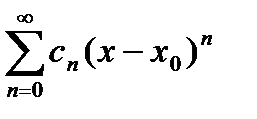 (4) функциялық қатарларды дәрежелі қатарлар деп атайды. Мұндағы
(4) функциялық қатарларды дәрежелі қатарлар деп атайды. Мұндағы  ,
,  сандары дәрежелі қатардың коэффициенттері деп аталады. (1)−қатардағы
сандары дәрежелі қатардың коэффициенттері деп аталады. (1)−қатардағы  немесе
немесе  ,
,  −тұрақты сан.Дәрежелі қатарлар арқылы анықталған интегралдарды берілген дәлдікпен есептеуге болады. Дәрежелі қатарлардың көмегімен дифференциалдық теңдеулерді жуықтап есептеуге болады.
−тұрақты сан.Дәрежелі қатарлар арқылы анықталған интегралдарды берілген дәлдікпен есептеуге болады. Дәрежелі қатарлардың көмегімен дифференциалдық теңдеулерді жуықтап есептеуге болады. ретті дифференциалдық теңдеудің (ДТ) жалпы түрі
ретті дифференциалдық теңдеудің (ДТ) жалпы түрі (1)
(1) −тәуелсіз айнымалы,
−тәуелсіз айнымалы,  −белгісіз функция,
−белгісіз функция, 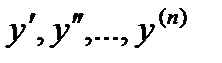 оның туындылары. (1) теңдеудегі туындының ең жоғарғы реті ДТ реті деп аталады. Егер
оның туындылары. (1) теңдеудегі туындының ең жоғарғы реті ДТ реті деп аталады. Егер  болса, онда
болса, онда (2)
(2)

 түрдегі теңдеу айнымалылары ажыратылатын теңдеу деп аталады. Бұл теңдеудің жалпы интегралы мынаған тең:
түрдегі теңдеу айнымалылары ажыратылатын теңдеу деп аталады. Бұл теңдеудің жалпы интегралы мынаған тең: кездейсоқ шамасының қабылдайтын мәндері ақырлы бүтін сандар немесе тізбек түрінде жазылса, онда
кездейсоқ шамасының қабылдайтын мәндері ақырлы бүтін сандар немесе тізбек түрінде жазылса, онда  ,
,  .
. ,
,  ,
, 
 ,
, 
 ,
, ,
,  .
.

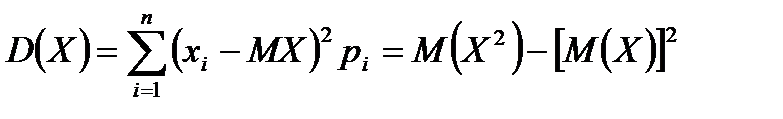 б) Үзіліссіз кездейсоқ шама үшін
б) Үзіліссіз кездейсоқ шама үшін 


 2`)
2`) 
 , мұндағы
, мұндағы  және
және  тәуелсіз кездейсоқ шамалар.
тәуелсіз кездейсоқ шамалар. ,
,  Анықтама.
Анықтама. шамасынорташа квадраттық ауытқудеп атайды. Анықтама.
шамасынорташа квадраттық ауытқудеп атайды. Анықтама. деп, оның ең ықтималды болатын мәнін айтады, ал үзіліссіз кездейсоқ шама үшін-
деп, оның ең ықтималды болатын мәнін айтады, ал үзіліссіз кездейсоқ шама үшін-  - ның максимум болатын нүктесі. Егер
- ның максимум болатын нүктесі. Егер  деп оның
деп оның  <
<  >
>  , болатын
, болатын  мәнін айтады.
мәнін айтады.
 Жазықтықтағы түзудiң нормаль түріндегі теңдеу
Жазықтықтағы түзудiң нормаль түріндегі теңдеу 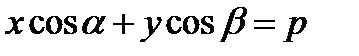


 және
және  түзулері берілсін
түзулері берілсін


 (5) формуланы Ньютон-Лейбниц формуласы дейді. Анықталған интегралдарды есептеу әдістері.
(5) формуланы Ньютон-Лейбниц формуласы дейді. Анықталған интегралдарды есептеу әдістері.
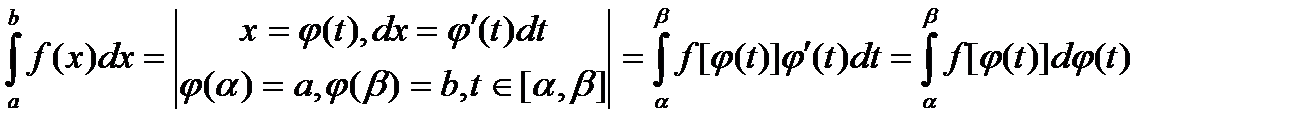 Жұп және тақ функцияларды интегралдау. Теорема.
Жұп және тақ функцияларды интегралдау. Теорема. 
 Жоғарғы ретті дифференциалдық теңдеулер. Реті төмендетілетін жоғарғы ретті дифференциалдық теңдеулер.
Жоғарғы ретті дифференциалдық теңдеулер. Реті төмендетілетін жоғарғы ретті дифференциалдық теңдеулер. 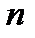 -ретті ДТ-ің жалпы түрі
-ретті ДТ-ің жалпы түрі 

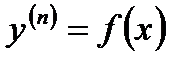 түріндегі теңдеулерді қарастырайық.
түріндегі теңдеулерді қарастырайық. екендігін ескеріп теңдеудің екі жағын
екендігін ескеріп теңдеудің екі жағын 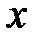 бойынша интегралдап
бойынша интегралдап 

 -ші ретті біртексіз сызықты ДТ-дің жалпы түрі
-ші ретті біртексіз сызықты ДТ-дің жалпы түрі
 теңдеуі
теңдеуі  -ші ретті біртекті сызықты ДТ деп аталады.Анықтама.
-ші ретті біртекті сызықты ДТ деп аталады.Анықтама.  интервалында
интервалында  функцияларын сызықты тәуелді дейміз.
функцияларын сызықты тәуелді дейміз.  (8) Егер (8) теңдік тек
(8) Егер (8) теңдік тек  үшін ғана орындалса, онда
үшін ғана орындалса, онда  функцияларын сызықты тәуелсіз дейміз.
функцияларын сызықты тәуелсіз дейміз.

 жалпы шешімі оның
жалпы шешімі оның  дербес шешімі мен оған сәйкес
дербес шешімі мен оған сәйкес  біртекті теңдеудің
біртекті теңдеудің  жалпы шешімінің қосындысына тең, яғни
жалпы шешімінің қосындысына тең, яғни  .
. оқиғасының жиілігі деп
оқиғасының жиілігі деп деп белгілесек, онда
деп белгілесек, онда  .
. -элементар оқиғалар кеңістігі,
-элементар оқиғалар кеңістігі,  - шектелген. Әрбір элементар
- шектелген. Әрбір элементар  оқиғасына
оқиғасына  санын сәйкес қойып, мұндай жағдай да элементар оқиғаларды тең мүмкіндікті,ал
санын сәйкес қойып, мұндай жағдай да элементар оқиғаларды тең мүмкіндікті,ал және
және  аймақтарының өлшемдері
аймақтарының өлшемдері  және
және  бар болса, лақтырылған нүктенің
бар болса, лақтырылған нүктенің  теңдігімен анықталады.
теңдігімен анықталады.  санын геометриялық ықтималдық деп атайды. Егер кесіндіні қарастырсақ,
санын геометриялық ықтималдық деп атайды. Егер кесіндіні қарастырсақ, 
 шеңбердiң канондық теңдеуi.
шеңбердiң канондық теңдеуi.
 эллипстiң канондық теңдеуi.
эллипстiң канондық теңдеуi.



 нақты сандар қосағын комплекс сандар деп атайды. егер олар үшін теңдік және қосу мен көбейту амалдар ұғымы былай анықталса:1Екі
нақты сандар қосағын комплекс сандар деп атайды. егер олар үшін теңдік және қосу мен көбейту амалдар ұғымы былай анықталса:1Екі  және
және  комплекс сандарды бір бірімен тең дейміз, тек сонда ғана, егер
комплекс сандарды бір бірімен тең дейміз, тек сонда ғана, егер  болса; 2Екі
болса; 2Екі  комплекс санын айтады.3Екі
комплекс санын айтады.3Екі  комплекс санын айтады.
комплекс санын айтады.  түрдегі комплекс сандарды алгебралық формадағы комплекс сан деп атайды.Енді теңдікті, қосу мен көбейту амалдарды былай жазуға болады.
түрдегі комплекс сандарды алгебралық формадағы комплекс сан деп атайды.Енді теңдікті, қосу мен көбейту амалдарды былай жазуға болады. 


 комплекс санды
комплекс санды  - түрдегі комплекс санды тригонометриялық формадағы комплекс сан деп атайды.
- түрдегі комплекс санды тригонометриялық формадағы комплекс сан деп атайды.  -комплекс санының аргументі,
-комплекс санының аргументі, 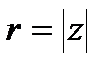 комплекс санының модулі.
комплекс санының модулі. 

 түрдегі комплекс санды көрсеткіштік формадағы комплекс сан деп атайды. Екі комплекс санды көбейткенде олардың модульдері көбейтіледі де, аргументтері қосылады, яғни
түрдегі комплекс санды көрсеткіштік формадағы комплекс сан деп атайды. Екі комплекс санды көбейткенде олардың модульдері көбейтіледі де, аргументтері қосылады, яғни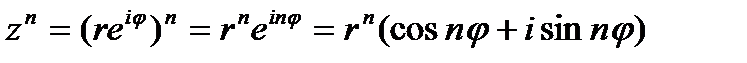 -формула Муаврдың формуласы деп аталады.
-формула Муаврдың формуласы деп аталады. Эйлер формулалары деп Крамер ережесі. Гаусс әдісі. Кері матрица әдісі.
Эйлер формулалары деп Крамер ережесі. Гаусс әдісі. Кері матрица әдісі.  белгiсiздерi бар
белгiсiздерi бар  (5) Осы жүйенiң негiзгi матрицасының анықтауышы
(5) Осы жүйенiң негiзгi матрицасының анықтауышы  . Бұл жағдайда
. Бұл жағдайда  кері матрица бар болады. (5) теңдіктің екі жағын сол жақтан
кері матрица бар болады. (5) теңдіктің екі жағын сол жақтан 

 (6)
(6)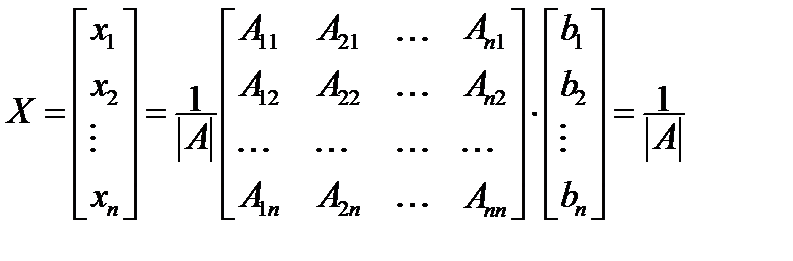

 (8) (8) өрнектерi Крамер формулалары деп аталады.
(8) (8) өрнектерi Крамер формулалары деп аталады. Кеңестіктегі түзудің ж/е жазықтықтың теңдеулері.
Кеңестіктегі түзудің ж/е жазықтықтың теңдеулері.
 ,
, 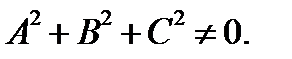 (3)
(3) векторы жазықтықтың нормалі деп аталады.
векторы жазықтықтың нормалі деп аталады. (4)
(4) (11)
(11) (12) түзудің параметрлі түріндегі теңдеулері.
(12) түзудің параметрлі түріндегі теңдеулері. осы (14) түзудің кеңістіктегі жалпы түрдегi теңдеулерi деп атайды.
осы (14) түзудің кеңістіктегі жалпы түрдегi теңдеулерi деп атайды.
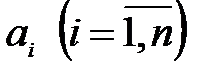 тұрақты сандар, коэффициенттері тұрақты сызықты біртекті ДТдеп аталады. ДТ-дің сипаттауыш теңдеуін аламыз:
тұрақты сандар, коэффициенттері тұрақты сызықты біртекті ДТдеп аталады. ДТ-дің сипаттауыш теңдеуін аламыз: (11) Егер
(11) Егер  (11) теңдеудің түбірі болса, онда
(11) теңдеудің түбірі болса, онда  (10) теңдеудің дербес шешімі болады және керісінше.а) Егер (11) теңдеудің түбірлері
(10) теңдеудің дербес шешімі болады және керісінше.а) Егер (11) теңдеудің түбірлері  әртүрлі нақты сандар болса, онда
әртүрлі нақты сандар болса, онда  функциялары (10) теңдеудің
функциялары (10) теңдеудің  сызықты тәуелсіз шешімі болады.Онда (10) теңдеудің жалпы шешімі
сызықты тәуелсіз шешімі болады.Онда (10) теңдеудің жалпы шешімі
 (13)Бұл теңдеудің жалпы шешімі
(13)Бұл теңдеудің жалпы шешімі  болады, мұндағы
болады, мұндағы  - (13) теңдеудің дербес шешімі, ал
- (13) теңдеудің дербес шешімі, ал  функциялар
функциялар  біртекті (10) теңдеудің іргелі жүйе шешімдері. Бұл шешімдерді табу әдісі жоғарыда көрсетілген. (13) теңдеудің оң жағы
біртекті (10) теңдеудің іргелі жүйе шешімдері. Бұл шешімдерді табу әдісі жоғарыда көрсетілген. (13) теңдеудің оң жағы ( 14)
( 14) және
және 
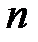 -ші және
-ші және  -ші дәрежелі коэффициенттері тұрақты көпмүшеліктер. (14) өрнектің дербес жағдайларын қарастырайық.
-ші дәрежелі коэффициенттері тұрақты көпмүшеліктер. (14) өрнектің дербес жағдайларын қарастырайық. болсын.
болсын. саны сипаттауыш теңдеудің түбірі болмасын. Онда (13) теңдеудің дербес шешімін
саны сипаттауыш теңдеудің түбірі болмасын. Онда (13) теңдеудің дербес шешімін  түрде іздейміз. Мұндағы
түрде іздейміз. Мұндағы 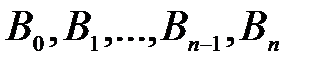 -дер белгісіз тұрақты коэффициенттер. Бұл (16) шешімді (13) теңдеуге қойып теңдіктің екі жағындағы бірдей дәрежелі
-дер белгісіз тұрақты коэффициенттер. Бұл (16) шешімді (13) теңдеуге қойып теңдіктің екі жағындағы бірдей дәрежелі 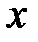 -тің алдындағы коэффициенттерін теңестіріп белгісіз
-тің алдындағы коэффициенттерін теңестіріп белгісіз  алгебралық теңдеулер жүйесін аламыз. Осы жүйеден белгісіз коэффициенттерді табамыз.
алгебралық теңдеулер жүйесін аламыз. Осы жүйеден белгісіз коэффициенттерді табамыз.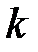 еселі түбірі болсын, онда (13) теңдеудің дербес шешімін
еселі түбірі болсын, онда (13) теңдеудің дербес шешімін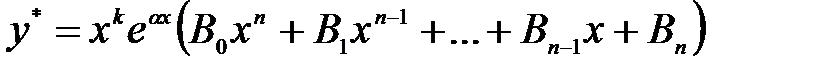 түрінде іздейміз.
түрінде іздейміз.