 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение допускаемых контактных напряжений.
Выбор материалов и термической обработки колес. При мелкосерийном производстве для изготовления колёс выбираем легированную сталь. Для шестерни сталь 40Х, термообработка-улучшение, твёрдость 269-302 НВ, средняя твёрдость НВ1=285; Для колеса сталь 40Х, термообработка-улучшение, твердость 235-262 НВ, средняя твёрдость НВ2=250.
Определение допускаемых контактных напряжений.
[σH] = σHlim ZN/SH, МПа, где σHlim-предел контактной выносливости при базовом числе циклов напряжений NH0, SH-коэффициент запаса прочности (SH=1,1), ZN-коэффициент долговечности.
Для шестерни σHlim1=2НВ1+70=2•285+70=640 МПа; Для колеса σHlim2=2НВ2+70=2•250+70=570 МПА
Базовое число циклов напряжений: Для шестерни NH1=30(HB1)2,4=30•2852,4≈2,3•107 Для колеса NH2=30(HB2)2,4=30•2502,4≈1,7•107
Расчетное число циклов напряжений за весь срок службы передачи при постоянном режиме нагружения: NK=60 n c Lh Где n-частота вращения шестерни, колеса, мин-1 с-число зацеплений зуба за один оборот колеса. Для нереверсивной передачи с=1. Lh-срок службы передачи Lh=2920 L Kг Кс Где L-число лет работы, L=5 лет; Kг-коэффициент годового использования передачи, Kг=0,85; Кс-число смен работы передачи в сутки, Кс=3. Lh=2920•5•0,85•3=37230 ч Расчетное число циклов напряжений: Для шестерни NK1=60n1c Lh=60•471,5•1•37230=105,3•107; Для колеса NK2=60n2c Lh=60•74,8•1•37230=16,7•107;
Для длительно работающих передач при NK> NH0 коэффициент долговечности равен:
Для шестерни Для колеса
Допускаемые контактные напряжения: Для шестерни [σH]1=640•0,82/1,1=477,1 МПа; Для колеса [σH]2=570•0,89/1,1=461,2 МПа.
Расчётное допускаемое контактное напряжение: [σH]=0,45([σH]1+[σH]2) ≥ [σH]2. [σH]=0,45(477,1+461,2)=422,2 МПа < [σH]2
Принимаем [σH]= [σH]2=461,2 МПа.
3.Определение допускаемых напряжений изгиба
[σF]= σFlim YR YZ YA YN/SF , МПа. Где σFlim - предел выносливости зубьев при изгибе соответствующий базовому числу циклов напряжений NF0. Для шестерни σFlim1=1,75•HB1=1,75•285≈498,7 МПа Для колеса σFlim2=1,75•HB2=1,75•250≈437,5 МПа
SF-коэффициент запаса прочности (SF =1,7 таб.4) YR - коэффициент, учитывающий влияние шероховатости переходной поверхности между зубьями. При шлифовании и зубофрезеровании с параметром шероховатости RZ ≤40 мкм (YR =1) YZ - коэффициент, учитывающий способ получения заготовки зубчатого колеса. (YZ=1) YА - коэффициент, учитывающий влияние двухсторонней приложенной нагрузки. При одностороннем приложении нагрузки (передача нереверсивная, YА=1,0 ). YN - коэффициент долговечности при расчёте зубьев на изгиб. YN= Где NF0 – базовое число циклов напряжений при расчёте на изгиб (NF0 =4•106); NK – расчетное число циклов напряжений за весь срок службы передачи. q – показатель степени кривой усталости (q=6 при твердости зубьев Н≤350 HB
Так как число циклов напряжений для шестерни NK1=173,2•107 и для колеса NK2=53,6•107 больше базового числа циклов NF0=4•106 , то принимаем YN =1. Допускаемые напряжения изгиба: [σF]1=498,7 •1•1•1•1/1,7=293 МПа [σF]2=437,5 •1•1•1•1/1,7=257 МПа
4.Определение межосевого расстояния.
U – передаточное число (U=4,8) T1 – вращающий момент на шестерне (Т1=120 Н•м) КН – коэффициент нагрузки. Для косозубых и шевронных передач КН=1,2 ᴪba – коэффициент ширины колеса. При несимметричном расположении косозубых колес относительно опор выбираем ᴪba=0,4.
Принимаем из ряда стандартных чисел
5. Определение модуля передачи.
Минимальное значение модуля из условий прочности на изгиб:
Km = 5,6•103 - для косозубой передачи; b2 – ширина венца колеса. b2= ᴪba aw=0,4•180=72,0 мм Принимаем b2=72 мм.
Максимальный допускаемый модуль передачи: Mnmax≈2aw/[17(4,8+1)]=2•180/17•5,8≈3,65 мм. Диапазон от 1,2 до 3,65 мм. Принимаем по ГОСТ 9563-80 стандартное значение нормального модуля mn=2 мм.
6. Определение суммарного числа зубьев шестерни и колеса.
ZS=2awcosβ/ mn
Где β – угол наклона зубьев колес; β > βmin=arcsin(4mn/b2)=arcsin(8/72)=6,37 Принимаем β=300. ZS=2•180 •0,866/2=155,88. Принимаем ZS=156. 7. Определение числа зубьев шестерни и колеса.
Число зубьев шестерни: Z1= ZS / (u+1) ≥ Z1min Z1min=17 cos3β=17•(0,866)3=11,04 Z1 =156/(4,8+1)=26,8 > Z1min Принимаем Z1=27. Так как Z1=27 >( Z1min+2)=14,то зубчатые колеса шевронной передачи изготовляются без смещения исходного контура (Х1=Х2=0).
Число зубьев колеса: Z2=ZS – Z1 для внешнего зацепления. Z2=156-27=129.
8. Уточнение передаточного числа. uф = Z2/Z1=129/27=4,77 Отклонение от заданного передаточного числа ∆u=100 |uф-u|/u=100•|4,77-4,8|/4,8=0,63% < [∆u]=3% 9. Уточнение угла наклона зубьев.
Cosβ= mn(Z1+Z2)/2aw=2(27+129)/2•180=0,86667; β=29,9620=29055`34``
10. Определение размеров зубчатых колес.
Делительный диаметр шестерни d1 и колеса d2: d1= mn Z1/соsβ=2•27/0,86667=62,307 мм; d2= mn Z2/соsβ=2•129/0,86667=297,691 мм.
Диаметры вершин зубьев шестерни da1 и колеса da2: da1= d1+2 mn=62,307+4=66,307 мм; da2= d2 - 2 mn=297,691 – 4=293,699мм.
Диаметры впадин зубьев шестерни df1 и колеса df2: df1= d1-2,5 mn=62,307 – 5=57,307 мм. df2= d2+2,5 mn=297,691-5=292,691 мм.
Ширина зубчатого венца шестерни b1 и колеса b2; b2=ᴪbaaw=0,4•180=72 b1=b2+5=77 мм.
11. Размеры заготовок. Диаметр заготовки шестерни Dзаг = da1+6=66,307+6=72,307 мм. Для колеса с выточками: толщина диска Сзаг=0,5 b2=0,5•77=38,5 мм. Sзаг=8 mn=8•2=16 мм.
Предельные размеры заготовок для стали 40Х: Dпр=125 мм; Sпр=125 мм (см табл.2) Условие пригодности заготовок выполняются, так как Dзаг < Dпр ; Сзаг < Sпр ; Sзаг < Sпр .
|




 =
=  =0,82;
=0,82; =
=  =0,89;
=0,89; ≥1
≥1 , мм.
, мм.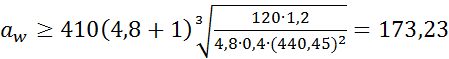 мм.
мм. = 180 мм.
= 180 мм.
 мм.
мм.