 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Знакоположительные ряды. Теоремы сравнения.
Лекция 5 Тема: Числовой ряд. Ряд из членов геометрической прогрессии. Необходимый признак сходимости ряда. Действие над рядами. Законоположительные ряды. Признаки сравнения. Определение ряда. Определение сходимости ряда. Примеры. Определение 1. Выражение вида Вначале будем изучать ряды, членами которых являются действительные числа. Приведем примеры рядов:
Определение 2. Ряд Пример 1. Исследовать на сходимость гармонический ряд Решение: Рассмотрим группу слагаемых
Отсюда следует, что Пример 2. Исследовать на сходимость ряд из членов геометрической прогрессии Решение: Рассмотрим частичную сумму данного ряда.
q (1-q) Если q Рассмотрим предел частичных сумм:
Остается рассмотреть случай, когда q=1. В этом случае имеем ряд а+а+а….,
Итак, ряд из членов геометрической прогрессии при Пример 3. Найти сумму ряда Решение. Данный ряд Пример 4. Исследовать на сходимость ряд Необходимый признак сходимости. Теорема 1. Если ряд т.е. Доказательство. По условию данный ряд сходится. Это означает, что
Следствие. Если общий член ряда к нулю не стремится, то ряд расходится. Действие над рядами. 1) Сложение рядов. Пусть даны два ряда
Теорема 2.Если ряды Доказательство. По условию ряды 2) Умножение ряда на число. Произведение ряда Теорема 3. Если ряд Если Доказательство. Справедливость теоремы вытекает из равенства: Теорема 4. Сходимость ряда не измениться если отбросить или прибавить конечное число первых членов ряда. Доказательство. Рассмотрим два ряда:
Справедливость теоремы вытекает из равенства:
Знакоположительные ряды. Теоремы сравнения. Ряд Теоремы, которые справедливы для знакоположительных рядов, справедливы для знакоотрицательных рядов, так, как умножение ряда на (-1), сходимость ряда не изменяет. Теорема 5: Для того, чтобы знакоположительный ряд сходился необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху. Доказательство. Дан знакоположительный ряд
Последовательность частичных сумм Теорема 6: Пусть даны два знакоположительных ряда Тогда если ряд (2) сходится, то ряд (1) тоже сходится. Если же ряд (1) расходится, то ряд (2) тоже расходится. Доказательство. Справедливость теоремы вытекает из неравенства Замечание 1. Учитывая теорему 3, можно утверждать, что теорема 5 справедлива при выполнении неравенств Чтобы применять теорему 5 при исследовании сходимости рядов, нужно иметь набор сходящихся и расходящихся рядов. Примером сходящихся рядов могут служить знакоположительные ряды из членов геометрической прогрессии при q Примером расходящегося ряда может служить гармонический ряд Ряды Дирихле: Ряды Дирихле мы исследуем позже с помощью интегрального признака Коши. А сейчас отметим, что ряды Дирихле при 1<S сходятся, а при S Ряд Дирихле при S=1 является гармоническим рядом. Пример 5:Исследовать на сходимость ряд Решение: 0 Пример 6:Исследовать на сходимость ряд Решение: Теорема 7: Пусть даны два знакоположительных ряда Пример 7:Исследовать на сходимость ряд Решение: так как Sinx Рассмотрим предел Следовательно, данный ряд сходится.
|



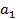 +
+  =
=  называется рядом,
называется рядом, 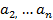 …- члены ряда,
…- члены ряда,  - общий член ряда.
- общий член ряда.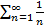 – гармонический ряд,
– гармонический ряд,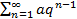 =
=  +
+  +…
+…  а - первый член прогрессии, q - знаменатель прогрессии.
а - первый член прогрессии, q - знаменатель прогрессии.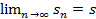 , где
, где  - сумма первых n членов ряда. Если
- сумма первых n членов ряда. Если  не существует, то ряд называется расходящимся.
не существует, то ряд называется расходящимся.

 , где каждая их скобок больше
, где каждая их скобок больше  .
. , т.е. предел не существует, т.к. при n
, т.е. предел не существует, т.к. при n  число скобок в
число скобок в  . Гармонический ряд расходится.
. Гармонический ряд расходится. , q
, q 



 то
то  .
. =
= 

 сходится и его сумма s=
сходится и его сумма s=  , а при
, а при  расходится.
расходится. .
. является рядом из членов геометрической прогрессии, где а=2, q=
является рядом из членов геометрической прогрессии, где а=2, q=  Так как
Так как  , то данный ряд сходится и s=
, то данный ряд сходится и s= 
 . Является рядом из членов геометрической прогрессии, где a=-2, q= -1. Так как
. Является рядом из членов геометрической прогрессии, где a=-2, q= -1. Так как  , то данный ряд расходится.
, то данный ряд расходится. .
. …
…  =
= 

 lim(
lim(  )=
)=  .
. Суммой двух рядов называется ряд
Суммой двух рядов называется ряд
 сходятся соответственно к
сходятся соответственно к  то ряд
то ряд  сходится к
сходится к  .
.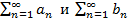 сходятся, то
сходятся, то  и
и 
 или числа
или числа  (3)
(3) .
. то оба ряда
то оба ряда  и
и 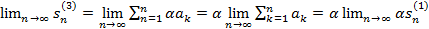
 +….+
+….+  +
+  …+
…+ 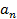 +… (4)
+… (4) +
+  +…+
+…+  =
=  +
+  ,где
,где  .
. ,
, 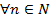 ,
,  =
=  …+
…+  …..
…..  ….
…. , неубывающая. Для того, чтобы неубывающая последовательность имела предел, необходимо и достаточно, чтобы она была ограничена сверху.
, неубывающая. Для того, чтобы неубывающая последовательность имела предел, необходимо и достаточно, чтобы она была ограничена сверху. для которых выполняются неравенства
для которых выполняются неравенства 

 =
=  …+
…+  +
+  +…
+…  =
=  и теоремы 4. В самом деле, если ряд (2) сходится, то последовательность {
и теоремы 4. В самом деле, если ряд (2) сходится, то последовательность {  не ограничена сверху и тем более
не ограничена сверху и тем более  не ограничена сверху. Следовательно, ряд (2) расходится.
не ограничена сверху. Следовательно, ряд (2) расходится. ,
,  .
. , а примерами расходящихся рядов могут быть знакоположительные ряды из членов геометрической прогрессии, при 1
, а примерами расходящихся рядов могут быть знакоположительные ряды из членов геометрической прогрессии, при 1 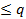 .
.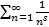
 расходятся.
расходятся. .
. ,
,  . Так как ряд Дирихле
. Так как ряд Дирихле  сходится, то по теореме сравнения данный ряд тоже сходится.
сходится, то по теореме сравнения данный ряд тоже сходится.
 <
< 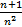
 Так как гармонический ряд расходится, то данный ряд тоже расходится.
Так как гармонический ряд расходится, то данный ряд тоже расходится. = c
= c 
 при x
при x  то данный ряд надо сравнить с рядом Дирихле
то данный ряд надо сравнить с рядом Дирихле  , который сходится.
, который сходится. = 1
= 1  0 в силу первого замечательного предела.
0 в силу первого замечательного предела.