Доказательство формулы Коши.
Лекция 12 Тема: Интегрирование функций комплексного переменного. Теорема Коши. Интеграл Коши. Особые точки. Вычеты. Интегрирование функций комплексного переменного. Пусть дана произвольная функция w=  комплексного переменного, определенная в некоторой области G комплексной плоскости переменного z, и Г-произвольная спрямляемая линия, лежащая в области G, с началом в точке B и концом в точке C. Кривую BC разобьем произвольным способом на n частей точками B=z0,z1,z2,…, zn=C .Это разбиение обозначим через (Т). Пусть комплексного переменного, определенная в некоторой области G комплексной плоскости переменного z, и Г-произвольная спрямляемая линия, лежащая в области G, с началом в точке B и концом в точке C. Кривую BC разобьем произвольным способом на n частей точками B=z0,z1,z2,…, zn=C .Это разбиение обозначим через (Т). Пусть  , , где  . В каждом из участков разбиения произвольным способом выберем по точке ζ1, ζ2,…, ζn и составим сумму . В каждом из участков разбиения произвольным способом выберем по точке ζ1, ζ2,…, ζn и составим сумму 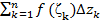 , которая называется интегральной суммой. Предел таких интегральных сумм при , которая называется интегральной суммой. Предел таких интегральных сумм при 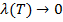 называется криволинейным интегралом от функции называется криволинейным интегралом от функции  по кривой Г. по кривой Г. 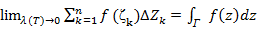 (1) (1)
Имеем:  тогда интеграл тогда интеграл  запишется в виде: запишется в виде:  (2) (2)
Формула (2) дает выражение интеграла по комплексному переменному через два криволинейных интеграла. Формулу (2) можно записать в следующем виде:  (3) (3)
Вычисление интеграла от функции комплексного переменного. Пусть кривая Г задана в виде  , тогда будем иметь: , тогда будем иметь:  
 , где , где 
Пример 1. Пусть Г- кусочно-гладкая кривая, соединяющая точки 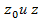 . Тогда . Тогда  интеграл интеграл 

Если Г замкнутая кривая, то  . . Основные свойства интеграла функции комплексного переменного 1.  , где Г+ и Г‑ один и тот же путь, который проходится в положительном и отрицательном (противоположном) направлении. , где Г+ и Г‑ один и тот же путь, который проходится в положительном и отрицательном (противоположном) направлении. 2.   3. 3. 
4.  5.  12.4. Теорема Коши. Вообще говоря,  по двум различным путям, соединяющим две точки В и С, может иметь различные значения, т.е. интеграл может зависеть от пути интегрирования. Как и в случае с криволинейным интегралом возникает вопрос: какие условия надо наложить на функцию по двум различным путям, соединяющим две точки В и С, может иметь различные значения, т.е. интеграл может зависеть от пути интегрирования. Как и в случае с криволинейным интегралом возникает вопрос: какие условия надо наложить на функцию  , чтобы , чтобы  не зависел от пути интегрирования. не зависел от пути интегрирования. Задача о независимости интеграла от пути интегрирования равносильна задаче нахождения условий, при которых данный интеграл, взятый по любому замкнутому контуру, равен нулю. Итак, предположим, что функция  является аналитической в односвязной области G, причем является аналитической в односвязной области G, причем  непрерывны вместе с частными производными первого порядка. непрерывны вместе с частными производными первого порядка. Так как  является функцией аналитической в области G, то в этой области выполняются условия Коши-Римана: является функцией аналитической в области G, то в этой области выполняются условия Коши-Римана:  На основании формулы (2) имеем: На основании формулы (2) имеем:  (4) (4)
Рассмотрим криволинейный интеграл  , для которого , для которого   . Так как . Так как  , ,  , то , то  в силу выполнения условий Коши-Римана и поэтому в силу выполнения условий Коши-Римана и поэтому  . Аналогично . Аналогично 
Учитывая (4), имеем:  Итак, доказана следующая теорема. Итак, доказана следующая теорема. Теорема Коши. Если  является аналитической функцией в односвязной области G и является аналитической функцией в односвязной области G и  непрерывны вместе с частными производными первого порядка, то интеграл от этой функции, взятый вдоль любого замкнутого контура, принадлежащего области G, равен нулю, т.е. непрерывны вместе с частными производными первого порядка, то интеграл от этой функции, взятый вдоль любого замкнутого контура, принадлежащего области G, равен нулю, т.е.  Теорема Коши является основной теоремой в теории аналитических функций. Теорема Коши остается справедливой, если потребовать только, что Теорема Коши является основной теоремой в теории аналитических функций. Теорема Коши остается справедливой, если потребовать только, что  является аналитической функцией в односвязной области G. является аналитической функцией в односвязной области G. Интеграл Коши Пусть G есть односвязная область, ограниченная кусочно-гладкой кривой Г, а  является аналитической в Ḡ. Это означает, что является аналитической в Ḡ. Это означает, что  является аналитической в некоторой области G’ содержащей G. является аналитической в некоторой области G’ содержащей G.  Формула Коши связывает значение функции во всякой внтутренней точке z области G со значениями данной функции на границе области G. Это означает, что значение аналитической функции на Г вполне определяют значения этой функции в области G. Формула Коши связывает значение функции во всякой внтутренней точке z области G со значениями данной функции на границе области G. Это означает, что значение аналитической функции на Г вполне определяют значения этой функции в области G.
Формула Коши имеет вид: 
Доказательство формулы Коши. Рассмотрим произвольную точку  и функцию и функцию 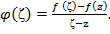 Функция Функция  является аналитической в области Ḡ, кроме точки является аналитической в области Ḡ, кроме точки  . Рассмотрим окружность γ с центром в точке z произвольно малого радиуса . Рассмотрим окружность γ с центром в точке z произвольно малого радиуса  такую, что γ лежит внутри G. Функция такую, что γ лежит внутри G. Функция  будет аналитической во всех точках, лежащих между контурами Г и γ, включая сами контуры. Можно доказать, что будет аналитической во всех точках, лежащих между контурами Г и γ, включая сами контуры. Можно доказать, что  (5) (5)
Последнее равенство показывает, что  не зависит от радиуса γ и является постоянным числом, равным не зависит от радиуса γ и является постоянным числом, равным  . Функция . Функция  стремится к определенному конечному пределу при стремится к определенному конечному пределу при  . Имеем: . Имеем: 
Если положить  становится непрерывной в Ḡ, т.е. становится непрерывной в Ḡ, т.е.  , такое, что , такое, что  . Учитывая последнее неравенство, будем иметь: . Учитывая последнее неравенство, будем иметь:
 ,откуда следует, что ,откуда следует, что  , т.к. , т.к.  можно взять сколь угодно малым, т.е. можно взять сколь угодно малым, т.е.

Но  Особые точки. Вычеты. Определение 1. Точка  называется изолированной особой точкой однозначной функции называется изолированной особой точкой однозначной функции  , если существует окрестность , если существует окрестность  точки точки  (с исключенной точкой (с исключенной точкой  ), в которой ), в которой  аналитична. аналитична. Различают три типа изолированных особых точек в зависимости от поведения функции  в их окрестности: в их окрестности: 1) Точка  называется устранимой особой точкой, если существует конечный предел называется устранимой особой точкой, если существует конечный предел  2) Точка  называется полюсом, если называется полюсом, если  является бесконечной большой при является бесконечной большой при  , т.е. , т.е.  3) Точка  называется существенно особой точкой, если называется существенно особой точкой, если  не существует.( кроме случая(2)). не существует.( кроме случая(2)). Определение 2. Вычетом функции  в изолированной особой точке в изолированной особой точке  называется число называется число  , которое обозначается , которое обозначается  , где , где  достаточно малая окружность достаточно малая окружность  , причём величина вычета не зависит от , причём величина вычета не зависит от  при достаточно малых при достаточно малых 
| 
 комплексного переменного, определенная в некоторой области G комплексной плоскости переменного z, и Г-произвольная спрямляемая линия, лежащая в области G, с началом в точке B и концом в точке C. Кривую BC разобьем произвольным способом на n частей точками B=z0,z1,z2,…, zn=C .Это разбиение обозначим через (Т). Пусть
комплексного переменного, определенная в некоторой области G комплексной плоскости переменного z, и Г-произвольная спрямляемая линия, лежащая в области G, с началом в точке B и концом в точке C. Кривую BC разобьем произвольным способом на n частей точками B=z0,z1,z2,…, zn=C .Это разбиение обозначим через (Т). Пусть  ,
, . В каждом из участков разбиения произвольным способом выберем по точке ζ1, ζ2,…, ζn и составим сумму
. В каждом из участков разбиения произвольным способом выберем по точке ζ1, ζ2,…, ζn и составим сумму 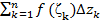 , которая называется интегральной суммой. Предел таких интегральных сумм при
, которая называется интегральной суммой. Предел таких интегральных сумм при 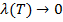 называется криволинейным интегралом от функции
называется криволинейным интегралом от функции  по кривой Г.
по кривой Г.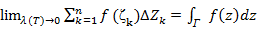 (1)
(1) тогда интеграл
тогда интеграл  запишется в виде:
запишется в виде: (2)
(2) (3)
(3) , тогда будем иметь:
, тогда будем иметь:

 , где
, где 
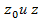 . Тогда
. Тогда  интеграл
интеграл

 .
. , где Г+ и Г‑ один и тот же путь, который проходится в положительном и отрицательном (противоположном) направлении.
, где Г+ и Г‑ один и тот же путь, который проходится в положительном и отрицательном (противоположном) направлении.
 3.
3. 


 является аналитической в односвязной области G, причем
является аналитической в односвязной области G, причем  непрерывны вместе с частными производными первого порядка.
непрерывны вместе с частными производными первого порядка. На основании формулы (2) имеем:
На основании формулы (2) имеем: (4)
(4) , для которого
, для которого 
 . Так как
. Так как  ,
,  , то
, то  в силу выполнения условий Коши-Римана и поэтому
в силу выполнения условий Коши-Римана и поэтому  . Аналогично
. Аналогично 
 Итак, доказана следующая теорема.
Итак, доказана следующая теорема. Формула Коши связывает значение функции во всякой внтутренней точке z области G со значениями данной функции на границе области G. Это означает, что значение аналитической функции на Г вполне определяют значения этой функции в области G.
Формула Коши связывает значение функции во всякой внтутренней точке z области G со значениями данной функции на границе области G. Это означает, что значение аналитической функции на Г вполне определяют значения этой функции в области G.
 и функцию
и функцию 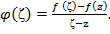 Функция
Функция  является аналитической в области Ḡ, кроме точки
является аналитической в области Ḡ, кроме точки  . Рассмотрим окружность γ с центром в точке z произвольно малого радиуса
. Рассмотрим окружность γ с центром в точке z произвольно малого радиуса  такую, что γ лежит внутри G. Функция
такую, что γ лежит внутри G. Функция  (5)
(5) не зависит от радиуса γ и является постоянным числом, равным
не зависит от радиуса γ и является постоянным числом, равным  . Функция
. Функция  . Имеем:
. Имеем:
 становится непрерывной в Ḡ, т.е.
становится непрерывной в Ḡ, т.е.  , такое, что
, такое, что . Учитывая последнее неравенство, будем иметь:
. Учитывая последнее неравенство, будем иметь: ,откуда следует, что
,откуда следует, что  , т.к.
, т.к.  можно взять сколь угодно малым, т.е.
можно взять сколь угодно малым, т.е.

 называется изолированной особой точкой однозначной функции
называется изолированной особой точкой однозначной функции  точки
точки 
 , т.е.
, т.е. 
 , которое обозначается
, которое обозначается  , где
, где  достаточно малая окружность
достаточно малая окружность  , причём величина вычета не зависит от
, причём величина вычета не зависит от 