 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Применение степенных рядов.
Лекция 9 Тема: Достаточные условия разложения функции в степенной ряд. Разложение функций Достаточные условия разложения функции в степенной ряд. Пусть дан степенной ряд S(x)= Задача: Зная функцию S(x), найти коэффициенты Степенной ряд в интервале сходимости можно почленно дифференцировать любое число раз. Поэтому будем иметь:
Отсюда вытекает, что необходимым условием разложения функции f(x) в степенной ряд по степеням
Степенной ряд в соотношении (1) называется рядом Тейлора функции f(x), а Однако существуют функции, которые бесконечно дифференцируемы в точке Для того, чтобы в соотношении (1) имею место равенство в некотором интервале Теорема 1. (Достаточные условия разложения функции в степенной ряд). Если на отрезке Пример 1. Разложить в ряд Маклорена функцию у= Решение. Функция Имеем
Так как А- произвольное, то равенство (2) справедливо для любого
Пример 2. Разложить в ряд Маклорена функцию y=sinx. Решение. y’(x)=cosx, y’’(x)=-sinx, y’’’(x)=-cosx, Пример 3. Разложить в ряд Маклорена функцию y=cosx. Решение.
Пример 4. Разложить в ряд Маклорена функцию y=ln(1+x) Решение. Имеем:
Пример 5. Разложить в ряд Маклорена функцию y=arctgx. Решение.
Пример 6. Разложить в ряд Маклорена функцию Решение.
Отметим, что при α натуральном последнее равенство справедливо Применение степенных рядов. Пример 7. Вычислить sin1 с точностью Решение. Имеем
Пример 8. Вычислить Решение. Неопределенный интеграл
Последнее равенство проинтегрируем почленно на отрезке [0,
|



 , sinx, cosx, ln(1+x), arctgx,
, sinx, cosx, ln(1+x), arctgx,  , в ряд Маклорена. Применение степенных рядов.
, в ряд Маклорена. Применение степенных рядов. , радиус сходимости которого R>0. Следовательно, в интервале сходимости ряд сходится к некоторой функции S(x), т.е.
, радиус сходимости которого R>0. Следовательно, в интервале сходимости ряд сходится к некоторой функции S(x), т.е.
 соответствующего степенного ряда.
соответствующего степенного ряда.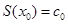 ,
,  ,
, 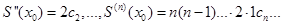

 является бесконечная дифференцированность функции в точке
является бесконечная дифференцированность функции в точке  , т.е
, т.е
 (1)
(1) называется рядом Маклорена для функции f(x)
называется рядом Маклорена для функции f(x) функция f(x) кроме бесконечной дифференцируемости в точке
функция f(x) кроме бесконечной дифференцируемости в точке  все производные функции по модулю ограничены одним числом,
все производные функции по модулю ограничены одним числом,  , то f(x) разлагается в ряд Тейлора, который сходится к f(x) на отрезке
, то f(x) разлагается в ряд Тейлора, который сходится к f(x) на отрезке  бесконечно дифференцируема на всей числовой оси и
бесконечно дифференцируема на всей числовой оси и  .
. . По теореме 1 функция y=
. По теореме 1 функция y=  разлагается в ряд Маклорена, который на отрезке [-A, A] сходится к данной функции.
разлагается в ряд Маклорена, который на отрезке [-A, A] сходится к данной функции.
 , (-∞,+∞) (2)
, (-∞,+∞) (2)
 ,…, следовательно
,…, следовательно  и функция y=sinx разлагается в ряд Маклорена
и функция y=sinx разлагается в ряд Маклорена  , который сходится к функции y=sinx.
, который сходится к функции y=sinx. 
 .
. . Функция y=cosx разлагается в ряд Маклорена, который сходится к функции y=cosx
. Функция y=cosx разлагается в ряд Маклорена, который сходится к функции y=cosx  .
.
 .
. , где|x|<1. Полученное равенство почленно проинтегрируем
, где|x|<1. Полученное равенство почленно проинтегрируем 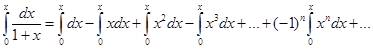 |x|<1.
|x|<1. |x|<1.
|x|<1.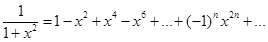 |x|<1. Полученное равенство почленно проинтегрируем при |x|<1.
|x|<1. Полученное равенство почленно проинтегрируем при |x|<1.  |x|<1.
|x|<1. |x|<1.
|x|<1.


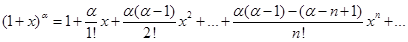 Можно доказать, что в общем случае последнее равенство справедливо при |x|<1.
Можно доказать, что в общем случае последнее равенство справедливо при |x|<1. =0,01.
=0,01. .
. 

 ,при этом ошибка будет равна
,при этом ошибка будет равна 
 называется остатком ряда.
называется остатком ряда.  . Если
. Если 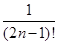 <0.01, то
<0.01, то 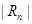 <0,01. Подберем наименьшее n, для которого
<0,01. Подберем наименьшее n, для которого  Следовательно,
Следовательно, 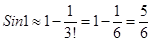 , причем ошибка будет меньше 0,01.
, причем ошибка будет меньше 0,01. с точностью
с точностью  не выражается в элементарных функциях, поэтому формулу Ньютона-Лейбница при вычислении данного интеграла применять нельзя.
не выражается в элементарных функциях, поэтому формулу Ньютона-Лейбница при вычислении данного интеграла применять нельзя.

 ].
].

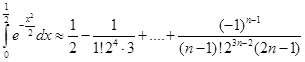 . Ошибка будет равна
. Ошибка будет равна  .
. . Если
. Если  <0,01, то и
<0,01, то и  .
.  . При этом ошибка будет меньше 0,01.
. При этом ошибка будет меньше 0,01.