 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Условия независимости криволинейного интеграла от пути интегрирования на плоскости.
Лекция 4 Тема: Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования. Формула Грина. Формула Грина устанавливает связь между криволинейным интегралом по замкнутому контуру Г на плоскости и двойным интегралом по области, ограниченной данным контуром. Замкнутый контур Г мы будем считать кусочно-гладким и без самопересечений. Криволинейный интеграл по замкнутому контуру Г обозначается символом Определение 1. Обход контура Г считается положительным, если при обходе контура Г область D остаётся слева. Г+ - контур Г обходится в положительном направлении, Г - - контур обходится в отрицательном направлении.
Теорема. Если P(x,y) и Q(x,y) непрерывны вместе со своими частными производными
Где Г= Г+ означает, что контур Г обходится в положительном направлении. Доказательство. Доказательство проведем для односвязной области D, т.е. Г=

Аналогично доказывается, что:
Из равенств (1) и (2) получаем:
Следовательно,
Формула Грина при сделанных предположениях доказана. Замечание 1. Формула Грина остаётся справедливой, если граница Г области D некоторыми прямыми, параллельными оси 0Х или 0Y пересекается более чем в двух точках. Кроме этого формула Грина справедлива и для n-связных областей. Условия независимости криволинейного интеграла от пути интегрирования на плоскости. В этом параграфе выясним условия, при выполнении которых криволинейный интеграл не зависит от пути интегрирования, а зависит от начальной и конечной точек интегрирования. Теорема 1. Для того, чтобы криволинейный интеграл Доказательство: Необходимость. Дано: Пусть в рассматриваемой области D взят произвольный кусочно-гладкий замкнутый контур Г. На контуре Г возьмем произвольные точки B и C.
 не зависит от пути интегрирования, то не зависит от пути интегрирования, то
Достаточность. Дано: Криволинейный интеграл Требуется доказать, что интеграл не зависит от пути интегрирования. Рассмотрим криволинейный интеграл по двум кусочно-гладким контурам, соединяющим точки B и С. По условию:
интеграл не зависит от пути интегрирования. Теорема 2. Пусть Доказательство: Достаточность. Дано:
Необходимость. Дано: По теореме 1 криволинейный интеграл Доказательство: Доказательство проведем от противного. Предположим, что
что противоречит условию, т.к. по условию криволинейный интеграл не зависит от пути интегрирования и по теореме 1. криволинейный интеграл по любому замкнутому контуру равен нулю.▼ |




 Замкнутый контур Г начинается в некоторой точке В этого контура и заканчивается в точке В. Интеграл по замкнутому контуру не зависит от выбора точки В.
Замкнутый контур Г начинается в некоторой точке В этого контура и заканчивается в точке В. Интеграл по замкнутому контуру не зависит от выбора точки В. в ограниченной замкнутой области D, то справедлива формула Грина:
в ограниченной замкнутой области D, то справедлива формула Грина:
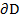
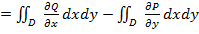 .
.

 (1)
(1) (2)
(2)
 не зависел от пути интегрирования в односвязной области необходимо и достаточно, чтобы этот интеграл, взятый по любому замкнутому кусочно-гладкому контуру в этой области равнялся нулю.
не зависел от пути интегрирования в односвязной области необходимо и достаточно, чтобы этот интеграл, взятый по любому замкнутому кусочно-гладкому контуру в этой области равнялся нулю. не зависит от пути интегрирования. Требуется доказать, что криволинейный интеграл по любому замкнутому кусочно-гладкому контуру равен нулю.
не зависит от пути интегрирования. Требуется доказать, что криволинейный интеграл по любому замкнутому кусочно-гладкому контуру равен нулю.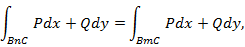


 , т.е.
, т.е.
 по любому замкнутому кусочно-гладкому контуру равен нулю.
по любому замкнутому кусочно-гладкому контуру равен нулю.
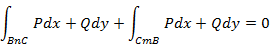
 т.е. криволинейный
т.е. криволинейный непрерывны вместе с частными производными
непрерывны вместе с частными производными  и
и  в односвязной области D. Для того, чтобы криволинейный интеграл
в односвязной области D. Для того, чтобы криволинейный интеграл  не зависел от пути интегрирования необходимо и достаточно, чтобы в области D выполнялось тождество
не зависел от пути интегрирования необходимо и достаточно, чтобы в области D выполнялось тождество 




 M0>α>0. По условию
M0>α>0. По условию  непрерывны в точке М0, поэтому существует круг u(М0,r) c центром в точке М0 некоторого радиуса r>0, который лежит в области D и в котором выполняется неравенство
непрерывны в точке М0, поэтому существует круг u(М0,r) c центром в точке М0 некоторого радиуса r>0, который лежит в области D и в котором выполняется неравенство 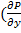 -
-  M0>α. Окружность с центром в точке М0 радиуса r обозначим через γ. По формуле Грина имеем:
M0>α. Окружность с центром в точке М0 радиуса r обозначим через γ. По формуле Грина имеем: ,
,