ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Найдем показания вольтметров с указанными типами преобразователей и видом входа.
Построить в соответствии с исходными данными в линейном масштабе график исследуемого сигнала и произвести его аналитическое описание. Запишем аналитическое выражение и построим график для заданного сигнала [с.14, 1] Сигнал u(t) можно описать системой уравнений, которая выглядит следующим образом: u(t)= Коэффициенты a, b, c, d определим из системы уравнений: 1. Найдем коэффициенты первой линейной функции
Откуда a=0;
2. Найдем коэффициенты второй линейной функции
Откуда
Полученные значения подставляем в систему:
Построим в соответствии с исходными данными в линейном масштабе график исследуемого сигнала
2. Найдем пиковое · Пиковое значение по формуле (7.1) из [2]
За время, равное периоду сигнала, максимальное значение численно равно заданному · Среднее значение по формуле (7.3) из [2]:
· Средневыпрямленное по формуле (7.2) из [2]:
· Среднеквадратическое по формуле (7.4) из [2]:
= Вычисление интегральных функций проводим на промежутках времени
Аналитическое описание переменной составляющей сигнала Аналитическое выражение переменной составляющей сигнала
График переменной составляющей сигнала:
График переменной составляющей сигнала смещен на значение Uср, относительно графика исходного сигнала. Найдем пиковое, среднее, средневыпрямленное и среднеквадратическое значения напряжения переменной составляющей заданного сигнала Для нахождения указанных значений необходимо аналитическое выражение для переменной составляющей сигнала подставить в интегральные выражения для нахождения среднего, средневыпрямленного и среднеквадратического значения напряжения переменной составляющей. · Пиковое значение:
Вычисление интегральных функций проводим на промежутках времени · Среднее значение по формуле (7.3) из [2]:
· Среднеквадратическое по формуле (7.4) из [2]:
· Средневыпрямленное Для вычисления средневыпрямленного значения сигнала необходимо определить время Т1 в которое происходит изменение знака функции Построим график модуля переменной составляющей сигнала
Найдем момент времени Т, в который график переменной составляющей меняет знак из уравнения
Вычисление функции
Определим коэффициенты амплитуды, формы, усреднения для исследуемого сигнала и его переменной составляющей.
Воспользуемся формулами (7.6),(7,7) и (7.8) из [1, стр. 25]: Для постоянной составляющей сигнала:
Соотношение Для переменной составляющей сигнала
Соотношение
Найдем показания вольтметров с указанными типами преобразователей и видом входа. Для вычисления показаний вольтметров воспользуемся соотношениями для градуировочных коэффициентов [2, стр.28], для вольтметров с преобразователем: пиковых значений средневыпрямленных значений среднеквадратических значений Показания вольтметров вычислим по формулам (5.11) из [3, стр. 90] для вольтметров с преобразователем: пиковых значений средневыпрямленных значений среднеквадратических значений 1) Вольтметр 1 – Преобразователь среднеквадратических значений с открытым входом. Вольтметр с открытым входом реагирует и переменную и на постоянную составляющую сигнала, значит :
2) Вольтметр 2 – преобразователь средневыпрямленных значений, закрытый вход. Вольтметр с закрытым входом реагирует только на переменную составляющую сигнала. значит:
3) Вольтметр 3 – преобразователь средневыпрямленных значений, открытый вход. Вольтметр с открытым входом реагирует и переменную и на постоянную составляющую сигнала, значит:
4) Вольтметр 4 – преобразователь пиковых значений, закрытый вход Вольтметр с закрытым входом реагирует только на переменную составляющую сигнала, значит :
|




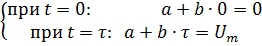






 , среднее
, среднее  , средневыпрямленное
, средневыпрямленное  и среднеквадратическое
и среднеквадратическое  значения напряжения наблюдаемого сигнала
значения напряжения наблюдаемого сигнала
 = 3,5 В.
= 3,5 В.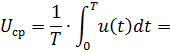
 В
В
 В
В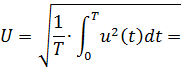

 и
и  .
.

 =1,371 В
=1,371 В
 можно получить, вычтя из выражения для сигнала u(t) среднее значения напряжения
можно получить, вычтя из выражения для сигнала u(t) среднее значения напряжения  (стр. 14[1])
(стр. 14[1])

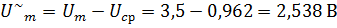



 .
.



 ,
,  и
и 

 В
В
 =
=  В
В


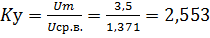
 справедливо для вычисленных коэффициентов.
справедливо для вычисленных коэффициентов.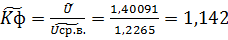

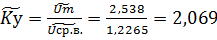
 справедливо для вычисленных коэффициентов.
справедливо для вычисленных коэффициентов.