 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Корреляционный анализ - математико-статистический метод выявления взаимозависимости компонент многомерной случайной величины и оценки тесноты их связи. 12
К. Пирсон и Дж. Юл разработали корреляционный анализ, который по их мнению должен ответить на вопрос о том, как выбрать с учетом специфики и природы анализируемых переменных подходящий измеритель статистической связи (коэффициент корреляции, корреляционное отношение, и т.д.), решить задачу, как оценить его числовые значения по уже имеющимся выборочным данным. Корреляционный анализ поможет: найти методы проверки того, что полученное числовое значение анализируемого измерителя связи действительно свидетельствует о наличии статистической связи; определить структуру связей между исследуемыми k признаками х 1, х 2,…, сопоставив каждой паре признаков ответ («связь есть» или «связи нет»). Парный коэффициент корреляции – основной показатель взаимозависимости двух случайных величин, служит мерой линейной статистической зависимости между двумя величинами., он соответствует своему прямому назначению, когда статистическая связь между соответствующими признаками в генеральной совокупности линейна. То же самое относится к частным и множественным коэффициентам корреляции. Парный коэффициент корреляции, характеризует тесноту связи между случайными величинами х и у, определяется по формуле:
Если р = 0, то между величинами х и у линейная связь отсутствует и они называются некоррелированными .Коэффициент корреляции, определяемый по вышеуказанной формуле, относится к генеральной совокупности. Частный коэффициент корреляции характеризует степень линейной зависимости между двумя величинами, обладает всеми свойствами парного, т.е. изменяется в пределах от -1 до +1. Если частный коэффициент корреляции равен ±1, то связь между двумя величинами функциональная, а равенство его нулю свидетельствует о линейной независимости этих величин.
28. Точечная и интервальная оценки коэффициента корреляции, проверка его значимости в корреляционном анализ. При построении доверительного интервала для неизвестного коэффициента корреляции
Распределение вероятностей значений
Статистика Асимптотически точный доверительный интервал надежности
где Доверительный интервал для математического ожидания
Величиной Доверительный интервал для гиперболического арктангенса коэффициента корреляции
Решение относительно
с границами, определяемыми как значения гиперболического тангенса Функция
29. Определение оценок параметров b0 и b1 двумерной линейной модели регрессии с помощью метода наименьших квадратов.Оценивание неизвестных коэффициентов модели регрессии методом наименьших квадратов. Теорема Гаусса – Маркова Определение коэффициентов модели регрессии осуществляется на третьем этапе схемы построения эконометрической модели. В результате этой процедуры рассчитываются оценки (приближенные значения) неизвестных коэффициентов спецификации модели. Спецификация линейной эконометрической модели из изолированного уравнения с гомоскедастичными возмущениями имеет вид:
Рассмотрим метод наименьших квадратов на примере оценивания эконометрических моделей в виде моделей парной регрессии (изолированных уравнений с двумя переменными). Если уравнение модели содержит две экономические переменные – эндогенную yiи предопределенную xi, то модель имеет вид:
Данная модель называется моделью линейной парной регрессии и содержит три неизвестных параметра: β0 , β1 , σ. (3) Предположим, что имеется выборка: (х1, y1), (х2, y2),… (хn , yn) (4) Тогда в рамках исследуемой модели данные величины связаны следующим образом: y1 = a0 + a1 * x1 + u1, y2 = a0 + a1 * x2 + u2, (5) … yn= a0 + a1 * x n + u n. Данная система называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели или схемой Гаусса-Маркова. Компактная запись схемы Гаусса-Маркова:
где
– вектор-столбец известных значений эндогенной переменной yiмодели регрессии;
– вектор-столбец неизвестных значений случайных возмущений εi;
– матрица известных значений предопределенной переменной xi модели; β = (β0 β1 )Т (10) – вектор неизвестных коэффициентов модели регрессии. Обозначим оценку вектора неизвестных коэффициентов модели регрессии как
Данная оценка вычисляется на основании выборочных данных (7) и (9) с помощью некоторой процедуры:
где P (X, ỹ) – символ процедуры. Процедура (12) называется линейной относительно вектора (7) значений эндогенной переменной yi, если выполняется условие:
где
(14) – матрица коэффициентов, зависящих только от выборочных значений (9) предопределенной переменной хi. Теорема Гаусса-Маркова. Пусть матрица Х коэффициентов уравнений наблюдений (6) имеет полный ранг, а случайные возмущения (8) удовлетворяют четырем условиям: E(ε1) = E(ε2) = … = E(εn) = 0, (15) Var(ε1) = Var(ε2) = … = Var(εn) = σ2(16) Cov(εi, εj) = 0 при i≠j(17) Cov(xi,εj) = 0 при всех значениях i и j (18) В этом случае справедливы следующие утверждения: а) наилучшая линейная процедура (13), приводящая к несмещенной и эффективной оценке (11), имеет вид:
б) линейная несмещенная эффективная оценка (19) обладает свойством наименьших квадратов:
в) ковариационная матрица оценки (19) вычисляется по правилу:
г) несмещенная оценка параметра σ2 модели (2) находится по формуле:
Следствие теоремы Гаусса-Маркова. Оценка
доставляемая процедурой (19) метода наименьших квадратов, может быть вычислена в процессе решения системы двух линейных алгебраических уравнений:
Данная система называется системой нормальных уравнений. Ее коэффициенты и свободные члены определяются по правилам: [x] = x1 + x2 +…+ xn, [y] = y1 + y2 +…+ yn, (24) x2] = x12 + x22 +…+ xn2, [xy] = x1*y1 + x2*y2 + … + xn*yn. Явный вид решения системы (23):
30 Проверка значимости и интервальное оценивание коэффициента регрессии b1 в регрессионном анализе. Для проверки значимости отдельных коэффициентов регрессии, т.е. гипотезы Н0: βj = 0, где j = 1, 2, ..., k, используют t-критерий и вычисляют tнабл(bj) = bj / Гипотеза H0 отвергается с вероятностью α, если tнабл > tкр. Из этого следует, что соответствующий коэффициент регрессии βj значим, т.е. βj ≠ 0. В противном случае коэффициент регрессии незначим и соответствующая переменная в модель не включается. Тогда реализуется алгоритм пошагового регрессионного анализа, состоящий в том, что исключается одна из незначительных переменных, которой соответствует минимальное по абсолютной величине значение tнабл. После этого вновь проводят регрессионный анализ с числом факторов, уменьшенным на единицу. Алгоритм заканчивается получением уравнения регрессии со значимыми коэффициентами. Существуют и другие алгоритмы пошагового регрессионного анализа, например с последовательным включением факторов. Наряду с точечными оценками bj генеральных коэффициентов регрессии βj регрессионный анализ позволяет получать и интервальные оценки последних с доверительной вероятностью γ. Интервальная оценка с доверительной вероятностью γ для параметра βj имеет вид
где tα находят по таблице t-распределения при вероятности α = 1 - γ и числе степеней свободы v = п - k - 1. Интервальная оценка для уравнения регрессии
Интервал предсказания
где tα определяется по таблице t-распределения при α = 1 - γ и числе степеней свободы v = п - k - 1. По мере удаления вектора начальных условий х0 от вектора средних
30. Рис. 53.2. Точечная
12 |




 используется специальная функция -
используется специальная функция -  -преобразование Фишера (гиперболический арктангенс) выборочного коэффициента корреляции r:
-преобразование Фишера (гиперболический арктангенс) выборочного коэффициента корреляции r: .
. - возрастающая нечетная функция: z(-r) = -z(r).
- возрастающая нечетная функция: z(-r) = -z(r). приближается (тем более точно, чем больше объем выборки n) нормальным распределением вероятностей
приближается (тем более точно, чем больше объем выборки n) нормальным распределением вероятностей  с параметрами:
с параметрами: и
и  .
. имеет асимптотическое стандартное нормальное распределение
имеет асимптотическое стандартное нормальное распределение  .
. для нормированного отклонения z:
для нормированного отклонения z: ,
, - квантиль уровня
- квантиль уровня  распределения
распределения  .
. :
: .
. в выражении
в выражении  можно пренебречь, принимая во внимание, что она при
можно пренебречь, принимая во внимание, что она при  есть бесконечно малая более высокого порядка в сравнении с
есть бесконечно малая более высокого порядка в сравнении с  .
. :
: .
. ,
, для значений
для значений  , равных соответственно
, равных соответственно  и
и  .
. задает преобразование, обратное
задает преобразование, обратное  .
.







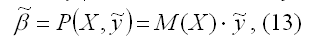


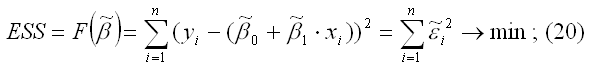





 bj. По таблице t-распределения для заданного α и v = п - k - 1 находят tкр.
bj. По таблице t-распределения для заданного α и v = п - k - 1 находят tкр. (53.19)
(53.19) в точке, определяемой вектором-столбцом начальных условий X0 = (1, x
в точке, определяемой вектором-столбцом начальных условий X0 = (1, x  , x
, x  ,,..., x
,,..., x  )T записывается в виде
)T записывается в виде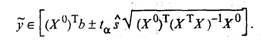 (53.20)
(53.20) (53.21)
(53.21) ширина доверительного интервала при заданном значении γ будет увеличиваться (рис. 53.2), где
ширина доверительного интервала при заданном значении γ будет увеличиваться (рис. 53.2), где  ).
).
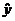 и интервальная
и интервальная  оценки уравнения регрессии
оценки уравнения регрессии  .
.