 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Комбинационные схемы (мультиплексоры, сумматоры, дешифраторы, шифраторы). 12
Сложение (сумма) по модулю 2 (Исключающее (логическое)_ИЛИ)
5) стрелка пирса (или-не)(↓)
6) штрих шеффера ( и-не)(∕)
Справедливы законы: 1)переместительный a+b=b+a; a*b=b*a 2) сочетательный а+(в+с)=(а+в)+с; а*(в*с)=(а*в)*с 3)распределительный а*(в+с)=а*в+а*с; а+(в*с)=(а+в)*(а+с) 4)Закон поглощения: а×(а+в)=а; а+а×в=а; а(а+в)(а+с)=а; а+ав+ас=а. 5)Закон склеивания: Для осуществления операций над логическими выражениями пользуются рядом тождеств: 1) А+А=А; 2) Теорема Де Моргана
Число переменных м.б. различным. Используя данные тождества можно упростить логические уравнения и свести к минимуму число логических элементов необходимых для реализации логич функции. Совокупность элементарных функций с помощью которых можно записать логическую функцию более сложного вида называется базисом. Синтез логич схем в базисе И-НЕ
Синтез логич схем в базисе ИЛИ-НЕ
Минимизация логических функций. Общие сведения. Диаграммы вейча Упрощение логических функций с помощью тождеств представляет трудности особенно при большем числе вх переменных. В этом случае приминяются методы минимизации: 1)диагр-мы Вейча, 2)Карты карно - предусматривает задание ФАЛ в виде координатных карт состояний. После записи ФАЛ в карту Карно сразу можно записать минимальную форму функции, что существенно уменьшает вероятность появления ошибки, 3)метод Квайна-Мак-Класки использование метода для функций с большим количеством аргументов и значительно уменьшает вероятность появления ошибки, 4)мет.неопред.коэфф Метод диаграмм Вейча Данный метод используется в основном для 2х, 3х, 4х 5ти переменных. Рассмотрим случай 4х переменных. В данном случае диаграмма состоит из 16ти возможных комбинаций вх переменных. На каждой клетке диаграммы обозначены значения каждой из 4х переменных. Рассмотрим этапы минимизации по диаграмме Вейча: 1.Задается некоторое логическое уравнение, которое необходимо преобразовать (исключить общие знаки инверсии, применить закон де Моргана, повторения, поглощения и склеивания) Привести к виду СДНФ, СКНФ 2.Заполнить диаграмму Вейча, если в данном выражении есть соответствующие комбинации вх переменных, то клетки диаграммы обозначаются единицей 3.Проводится склейка клеток, т.е. можно объединить целую заполненную строку, целый столбец, полстроки, полстолбца. Можно склеивать соседние строки, столбцы, полустроки, полустолбцы. Можно объединять нижний, верхний, правый и левый края. Нельзя соединить нечетное число клеток клетки по диагонали. 4.Расшифровка склеек. Каждая склейка в результате должна быть представлена в виде конъюнкции переменных. В результате расшифровок склеек получаем результат минимизации, т.е. новое упрощенное логическое выражение. 5. Строится новая логическая схема, в выбранном базисе. ПРИМЕР
заполняем клетки диаг-мы Вейча:
Склейка: Результат минимизации Строим лог схему:
Комбинационные схемы (мультиплексоры, сумматоры, дешифраторы, шифраторы). Комб устр-ва – устр-ва в кот состояние выхода в данный момент времени зависит от сост входа в данный момент времени. К ним относят: шифраторы (кодеры), дешифраторы (декодеры), мультиплексоры, демультиплексоры, цифр-ые сумматоры, цифр-ые компараторы, схемы сравнения. Дешифратор (DC)(декодерами) комб.лог.устр-во для преобраз-я чисел двоич. Код в унитарный. Каждому двоичному числу на входе соот-ет сигнал на определенном выходе деш-ра. Входы дешифратора называют адресными. Соотношение входов (n) и выходов (m): Если на вход подается код 1010, то логическая единица появится на 10-м выходе, а на всех остальных выходах будет 0 сигнал. (если выходы инверсные то появится 0, а на остальных единицы)
Шифратор (СD).Комбинационное логич.устр-во для преобраз-я чисел из десятич.с-мы в двоичную
у3=x4+x5+x6+x7; y2=x2+x3+x6+x7; y1=x1+x3+x5+x7
Мультиплексоры. Мультиплексором – комб.устройство, в котором единств выход соед с 1 из информ.входом в соответствии с кодом адреса.
Если x=0 , y=0, т.е. код адреса 00 DO – DATA OUTPUT (инф. выход) DI –DATA INPUT (инф. вход) Функция описывающая работу мультиплексора:
Сумматоры. Сумматор – это устройство для сложения двоичных слов. Правило сложение двоичных чисел: сложение осуществляется поразрядно от младшего разряда к старшему. В младшем разряде вычисляется сумма младших разрядов слагаемых А1 и В1. Эта сумма может быть записана однозначным числом S1, либо двухзначным числом P1 S1 (Р-перенос; S-сумма). В следующих разрядах находится сумма разрядов слагаемых Аi и Вi, причем если Рi–1=1, то к данной сумме добавляется еще перенос. Одноразрядный сумматор состоит из 2х комбинационных схем: одна для формирования Si, другая для формирования Рi. Полусумматором – комбинационное устройств с двумя входами и двумя выходами, которое отличается от одноразрядного сумматора отсутствием сигнала Рi–1 (перенос из соседнего младшего разряда в данных). Рис а – на основе одноразрядного сумматора построим 3-х разрядный сумматор.
12 |









 ;
; 
 ; 3) А+0=А; 4) А+1=1; 5) А×А=А; 6)
; 3) А+0=А; 4) А+1=1; 5) А×А=А; 6)  ; 7) А×0=0; 8) А×1=А; 9)
; 7) А×0=0; 8) А×1=А; 9)  ; 10)
; 10)  ;
; ;
;  (идет разрыв и меняем знак).
(идет разрыв и меняем знак).

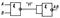











 (для полного дешифратора). Для неполного
(для полного дешифратора). Для неполного  . Дешифратор реализует следующие логические функции.
. Дешифратор реализует следующие логические функции. 

 . Обратное дешифратору.
. Обратное дешифратору. .
.
