 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Определение числа фаз, независимых компонентов и степеней свободы
Исследование 1 Для удобства последующих расчётов составляем таблицу исходных данных, используя материал [1-3]. Таблица 2 Исходные данные для термодинамического исследования реакции 2BiF3+3H2=2Bi+6HF
1.1.1.Расчёт изменения изобарной теплоемкости Зависимость теплового эффекта реакции от температуры определяется законом Кирхгофа
где Последняя величина рассчитывается по уравнению
где Cp,i – мольная изобарная теплоёмкость i-го вещества, определяемая из уравнения Cp,i = ni-стехиометрический коэффициент i-го вещества в равнении реакции. Для исследуемой реакции, после подстановки в уравнение (2) ni, оно примет вид ∆Cр= Определим температурные зависимости Cp,i:
Определим расчётные уравнения
Рассчитаем значения Таблица 3 Величина 2BiF3+3H2=2Bi+6HF
График зависимости ∆Cp=f(T)
Определим значение
Уравнение (7) имеет вид
или в числовом виде
Рассчитаем
Таблица 4 Величина 2BiF3+3H2=2Bi+6HF
График зависимости ∆
Расчёт изменения энтропии реакции Изменение энтропии системы определяется по уравнению
Значение
Рассчитаем
Рассчитаем по этому уравнению изменения энтропии для температур 400, 420, 440, 460, 480, 500, 520, 540К. Таблица 5 Величина 2BiF3+3H2=2Bi+6HF График зависимости ∆
Расчёт изменения стандартной энергии Гиббса При расчёте изменения стандартной энергии Гиббса для реакции воспользуемся уравнением Гиббса-Гельмгольца
Таблица 6 Значения изменения стандартной энергии Гиббса при различных температурах
График зависимости ∆
Вывод уравнения зависимости константы равновесия от температуры Константа равновесия связана с изменением стандартной энергии Гиббса соотношением ln Kp = - После подстановки выражения (13) в уравнение (14) получим ln Kp = -
Уравнение (15) можно записать в виде ln Kp = (A/T) + B, (16) где А и В – постоянные, которые соответственно равны: A = - B = Уравнение (16) отвечает линейной зависимости ln Kp = f(1/T). Таблица 7 Величины констант равновесия при различных температурах
График зависимости LnKp от обратной температуры
A = tga = ln Определим численное значение B B = lnKp1 – A*1/T1 =0,102+(3316*2*10⁻³)=6,734 Приближенное уравнение зависимости константы равновесия от температуры имеет вид lnKp =-3316/Т+6,734 По значениям коэффициентов А и В рассчитаем величину среднего теплового эффекта реакции
Исследование 2 В этом исследование нужно для рассматриваемой системы рассчитать число степеней свободы, определить возможное направление протекания реакции при заданных условиях, а также состав газовой фазы системы в состоянии равновесия
Определение числа фаз, независимых компонентов и степеней свободы Рассматриваемая система состоит из трёх фаз : двух твёрдых фаз BiF3 и Bi, а также одной газообразной, представляющей смесь газов H2 и HF. Итак, ф=3.
Связь между веществами, входящими в рассматриваемую систему, выражается уравнением реакции. Следовательно, k = m – r = 4-1 = 3. (20) Число степеней свободы равно числу параметров системы, которые можно изменить в некоторых пределах так, чтобы число и природа фаз оставались прежними. По правилу фаз Гиббса C = k + n – ф , (21) где n – число внешних параметров, влияющих на состояние равновесия системы. Обычно это давление и температура, т.е n = 2.
Для рассматриваемой системы c = k + 2 – ф = 3+2-3 =2. |



 кДж/моль
кДж/моль Дж/моль*К
Дж/моль*К *10^-5
*10^-5 и теплового эффекта реакции
и теплового эффекта реакции 
 (1)
(1) - стандартный тепловой эффект реакции при 298 К;
- стандартный тепловой эффект реакции при 298 К;  - изменение теплоёмкости системы в результате протекания реакции.
- изменение теплоёмкости системы в результате протекания реакции. (2)
(2) (3)
(3) . (4)
. (4)
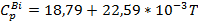


 Для чего подставим уравнения (5a, 5b, 5c, 5d) в уравнение (4)
Для чего подставим уравнения (5a, 5b, 5c, 5d) в уравнение (4) Cp =[6*(26,92+3,43*
Cp =[6*(26,92+3,43*  +1,09*
+1,09*  )+(2*(18,79+22,59*
)+(2*(18,79+22,59*  =-63,62-9,78*
=-63,62-9,78*  при различных температурах: 400, 420, 440, 460, 480, 500,520, 540К.
при различных температурах: 400, 420, 440, 460, 480, 500,520, 540К.

 (7)
(7) ) (8)
) (8) =195900Дж.
=195900Дж.

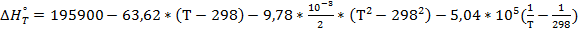
 при различных температурах для реакции
при различных температурах для реакции =f(T)
=f(T)
 (10)
(10) определяется по формуле
определяется по формуле (11)
(11)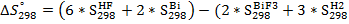 )= (6
)= (6  173,86+ 2
173,86+ 2  (12)
(12) при различных температурах для реакции
при различных температурах для реакции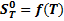
 Дж/К
Дж/К
 . (13)
. (13)





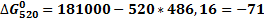

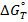
 =f(T)
=f(T)
 . (14)
. (14) . (15)
. (15)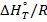 ; (17)
; (17) ,
, 

 = 0,102-1,76/2-2,5*10³=-3316
= 0,102-1,76/2-2,5*10³=-3316 и изменение энтропии
и изменение энтропии  . Согласно уравнениям (17)-(18) имеем :
. Согласно уравнениям (17)-(18) имеем : 3316*8,31=27555,96Дж.
3316*8,31=27555,96Дж. 6,734*8,31=55,95
6,734*8,31=55,95