 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Решение задачи методом полного перебора 12
Введение Для вычисления числовых параметров, характеризующих стохастические объекты, нужно построить некоторую вероятностную модель явления, учитывающую сопровождающие его случайные факторы. Для математического описания многих явлений, развивающихся в форме случайного процесса, может быть с успехом применен математический аппарат, разработанный в теории вероятностей для так называемых марковских случайных процессов. Пусть имеется некоторая физическая система S, состояние которой меняется с течением времени (под системой S может пониматься что угодно: техническое устройство, ремонтная мастерская, вычислительная машина и т.д.). Если состояние Sменяется по времени случайным образом, говорят, что в системе Sпротекает случайный процесс. Примеры: процесс функционирования ЭВМ (поступление заказов на ЭВМ, вид этих заказов, случайные выходы из строя), процесс наведения на цель управляемой ракеты (случайные возмущения (помехи) в системе управления ракетой), процесс обслуживания клиентов в парикмахерской или ремонтной мастерской (случайный характер потока заявок (требований), поступивших со стороны клиентов). Случайный процесс называется марковским процессом (или «процессом без последствия»), если для каждого момента времени t0вероятность любого состояния системы в будущем (при t>t0) зависит только от её состояния в настоящем (при t= t0) и не зависит от того, когда и каким образом система пришла в это состояние (т.е. как развивался процесс в прошлом). Пусть S техническое устройство, которое характеризуется некоторой степенью изношенности S. Нас интересует, как оно будет работать дальше. В первом приближении характеристики работы системы в будущем (частота отказов, потребность в ремонте) зависят от состояния устройства в настоящий момент и не зависят от того, когда и как устройство достигло своего настоящего состояния. Расчетно-графическая работа выполняется с помощью программы ²Оптимальное моделирование и управление в системах марковского типа². Программа написана на алгоритмическом языке VISUAL BASIC и оформлена в виде модуля табличного процессора EXCEL. Программа позволяет решать задачи марковского типа с помощью метода полного перебора и метода итераций. Решение задачи методом полного перебора
Метод полного перебора основан на переборе всех стационарных стратегий Для запуска программы надо загрузить в табличный процессор EXCEL файл mark.xls. При открытии файла активируется лист Метод полного перебора, содержащий талицы и 1 управляющую кнопку: 1) “Создать таблицы”; Для начала работы с программой необходимо заполнить исходную таблицу на листе Метод полного перебора. В исходную таблицу вводятся следующие значения: 1) число альтернатив управления; 2) число состояний системы; После заполнения исходной таблицы нужно нажать кнопку "Создать таблицы". На лист Метод полного перебора будут выведены следующие таблицы для ввода исходных данных задачи марковского типа: 1) "Начальные вероятности состояний системы; 2) "Возможные стратегии" – таблица для ввода правил, в соответствии с которыми на каждом шаге марковского процесса выбирается управленческая альтернатива в зависимости от состояния системы; 3) "Матрицы переходных вероятностей" - таблица для ввода всех переходных вероятностей, т.е. условных вероятностей того, что из состояния i в результате испытания система перейдет в состояние j; 4) "Матрицы доходов"; 5) "Ожидаемый одношаговый доход"; 6) "Стационарные вероятности"; 7) "Оптимальный доход"; 8) "Максимальный доход " Вид экрана с таблицами для ввода исходных данных задачи марковского типа представлен ниже: Таблица 1.
Таблица 2.
Таблица 3.
Таблица 4-19.
Для того, чтобы начать делать расчеты, необходимо таблицы, представленные выше. Данные для начальных вероятностей системы, матриц переходных вероятностей 1 и 2 и матриц доходов 1 и 2 берутся из лабораторной работы «Оптимальное моделирование и управление в системах марковского типа». Таблица «Возможные стратегии заполняется следующим образом: Таблица 20.
Далее для каждой стационарной стратегии формируем матрицы переходных вероятностей 3-8 и матрицы доходов 3-8. Для этого необходимо модернизировать состояния согласно возможным стратегиям поведения. Сформируем матрицу переходных вероятностей 3 и матрицу дохода 3. В таблице «Возможные стратегии» стационарной стратегии 3 соответствуют состояния 2, 1, 1:
Матрицы переходных вероятностей и матрицы дохода 1 и 2 заданы и имеют вид:
Например, формируя матрицу переходных вероятностей 3 и матрицу дохода 3, мы модернизируем состояние 1. Таким образом, матрицы будут иметь следующий вид:
Аналогично будут сформированы и остальные матрицы переходных вероятностей и матрицы доходов:
Метод полного перебора включает в себя 4 шага: 1. Вычисляем ожидаемый одношаговый доход
Результаты вычислений заносим в таблицу:
2. Вычисляем стационарные вероятности матрицы переходных вероятностей из уравнений
Убираем из каждой системы уравнения одно любое уравнение и находим решение системы уравнений методом обратной матрицы с использованием встроенных функций Excel (в нашем случае из системы уравнений (страт_1) убираем второе уравнение, из системы уравнений (страт_2) убираем третье уравнение). Для нахождения решений используется формула:
Результаты решения систем уравнений заносим в таблицу:
Далее формируем согласно возможным стратегиям стационарные вероятности для стратегий 3-8:
3. Определяем ожидаемый доход
4. Выбираем максимальное значение среди одношаговых доходов (max
Таким образом, получаем оптимальную стратегию:
12 |



 по формуле:
по формуле:
 - ожидаемый одношаговый доход;
- ожидаемый одношаговый доход; – переходная вероятность – условная вероятность того, что из состояния i в результате испытания система перейдет в состояние j;
– переходная вероятность – условная вероятность того, что из состояния i в результате испытания система перейдет в состояние j; – значение i доходности
– значение i доходности :
:
 - матрица переходных вероятностей;
- матрица переходных вероятностей; - стационарная вероятность
- стационарная вероятность

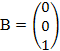

 для стратегии S по формуле:
для стратегии S по формуле: