 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Нахождение особых решений уравнений, 12
Не разрешенных относительно производной В этом параграфе рассматриваются два метода нахождения особых решений уравнений вида
Метод p - дискриминанта Приведем теорему существования и единственности решения для уравнения, не разрешенного относительно производной. Теорема. Существует единственное решение
определенное в некоторой окрестности точки
1) 2) производная 3) существует ограниченная по модулю производная В точках особого решения должно быть нарушено по крайней мере одно из условий этой теоремы. В дифференциальных уравнениях, встречающихся в прикладных задачах, условия 1) и 3) обычно выполняются, но условие
Обычно заменяют
Исключая из этих уравнений
Определение. Множество точек Дискриминантная кривая может состоять из одной или нескольких кри- вых. Если уравнение (1) имеет особое решение, то оно находится среди этих Заметим, что в точках, удовлетворяющих уравнению (3), не обязательно нарушается единственность решения уравнения (1). Это следует из того, что условия теоремы являются только достаточными для единственности решения, но не необходимыми и, следовательно, нарушение какого - нибудь условия теоремы дает только необходимые условия существования особого решения. В
Геометрическое место точек заострения может являться интегральной кривой и в этом случае оно является особым решением.
Из сказанного выше следует, что для нахождения особых решений уравнения (1) требуется: 1) найти 2) выяснить путем непосредственной подстановки в уравнение (1), есть ли среди ветвей 3) для отобранных решений проверить выполнение определения особого решения. Для того чтобы интегральная кривая есть в каждой своей точке она касалась некоторой кривой из семейства интегральных кривых
Если для каждого Пример 17. Выяснить, имеют ли особые решения уравнения: а) ▲ а)
Исключая Непосредственной подстановкой в уравнение, убеждаемся, что б) Составим систему уравнений, определяющую
Исключая уравнение убеждаемся, что Найдем общее решение уравнения:
Ни одна кривая из семейства интегральных кривых не пересекает ось в)
Исключая
Рассмотрим на кривой
Эта система совместна для любого Изобразите особое решение и одну из интегральных кривых, соответствующих значению Метод В этом пункте понятие особого решения уравнения (1) связывается с по- нятием огибающей семейства интегральных кривых. Определение. Огибающей семейства линий Пусть общий интеграл уравнения (1) есть
и это семейство интегральных кривых дифференциального уравнения имеет огибающую. Легко убедиться, что огибающая семейства (5) является особым решением уравнения. Действительно, в точках огибающей значения Из дифференциальной геометрии известно, что для нахождения огибающей семейства кривых
Исключая
которое определяет Таким образом, чтобы найти особое решение с помощью стемой (6). Ветвь этой кривой, являющаяся решением уравнения (1), будет особым решением. Пример 18. Найти особое решение уравнения
▲ Общий интеграл этого уравнения имеет вид
Находим
Пример 19. Доказать, что уравнение Клеро (§4, п.4.3)
имеет особое решение, которым является его частное решение
▲ Общее решение уравнения Клеро
Сравнивая частное решение (9) с что они совпадают. Частное решение (9), являясь огибающей семейства прямых (10), будет особым решением уравнения Клеро. ▲ 12 |



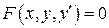 . (1)
. (1) уравнения
уравнения и удовлетворяющее условию
и удовлетворяющее условию  , для которого
, для которого  где
где  – один из действительных корней уравнения
– один из действительных корней уравнения  функция
функция  удовлетворяет условиям:
удовлетворяет условиям: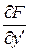 существует и отлична от нуля;
существует и отлична от нуля; .
. часто нарушается. Итак, в точках особого решения должны одновременно выполняться два условия:
часто нарушается. Итак, в точках особого решения должны одновременно выполняться два условия: .
.
 и рассматривают систему уравнений
и рассматривают систему уравнений (2)
(2) , получаем уравнение
, получаем уравнение . (3)
. (3) (кривая на плоскости), определяемое уравнением
(кривая на плоскости), определяемое уравнением 

 была особой, то
была особой, то , требуется, чтобы для
, требуется, чтобы для  выполнялись условия
выполнялись условия (4)
(4) существует хотя бы одно решение
существует хотя бы одно решение  этой системы, то решение
этой системы, то решение  является особым решением уравнения (1).
является особым решением уравнения (1). б)
б)  в)
в)  .
.
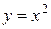 .
.
 . Непосредственной подстановкой в
. Непосредственной подстановкой в ,
,  ,
,  ,
,  .
. . Отсюда следует, что в точках интегральной кривой
. Отсюда следует, что в точках интегральной кривой 
 – дискриминантная кривая., причем, она является решением уравнения (см. пр. 11). Проверим, является ли это решение особым, то есть касаются ли его в каждой точке другие решения. В пункте 4.1 (пр. 11) было найдено, что семейство интегральных кривых задается формулой
– дискриминантная кривая., причем, она является решением уравнения (см. пр. 11). Проверим, является ли это решение особым, то есть касаются ли его в каждой точке другие решения. В пункте 4.1 (пр. 11) было найдено, что семейство интегральных кривых задается формулой .
.
 . Действительно, из второго уравнения системы
. Действительно, из второго уравнения системы  . Это равенство справедливо для всех
. Это равенство справедливо для всех  , которая касается особого решения в точке
, которая касается особого решения в точке 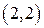 . ▲
. ▲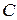 - дискриминанта
- дискриминанта называется линия, которая в каждой своей точке касается какой - нибудь из линий семейства, причем в различных своих точках она касается разных линий семейства.
называется линия, которая в каждой своей точке касается какой - нибудь из линий семейства, причем в различных своих точках она касается разных линий семейства. совпадают со значениями
совпадают со значениями  . и, так как огибающая вся состоит из точек касания, следовательно, в каждой точке огибающей значение
. и, так как огибающая вся состоит из точек касания, следовательно, в каждой точке огибающей значение  (6)
(6) , (7),
, (7), , определяемую си-
, определяемую си- .
.
 - дискриминант:
- дискриминант:
 .
.

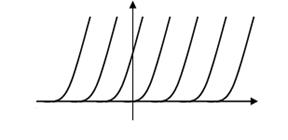
 (8)
(8) (9)
(9) (10)
(10) (11)
(11)