 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Учёт фактора времени при формирования и реализации финансовой политики организации
Изменение ценности денег во времени объясняется тем, что денежная единица сегодня стоит дороже, чем через определенный промежуток времени. Это удорожание денежной единицы происходит по нескольким причинам: - на деньги, полученные сегодня, можно получить доход в будущем; - покупательная способность денег с течением времени снижается из-за инфляции; - вложение денег во что-либо означает отказ от текущего потребления; - есть риск невозврата денег, если ожидается получить их «завтра». Поскольку деньги меняют свою ценность во времени, сравнивать затраты и выгоды напрямую нельзя. Необходимо привести все расчеты к единой временной точке сопоставления. Для этого существуют специальные приемы. Математические основы формирования финансовой политики Управление финансами организации сопряжено с проведением большого количества расчетов, связанных с различиями в величине денежных средств в разные периоды времени. В этой связи большое значение приобретает оценка стоимости денег во времени, отражающая основную концепцию финансового менеджмента. Большую роль в стоимостной оценке денег играют методы расчета процентных ставок, среди которых различают простые и сложные проценты, процентные и учетные ставки. Одно из важнейших базовых понятий теории количественного финансового менеджмента — понятие «процент». Процент — это доход (от англ. interest), в данном случае это абсолютная величина, выраженная в денежных единицах, а не в долях единицы. Если в инвестиционный проект в начале периода была вложена сумма P, а по завершении этой операции получена сумма S, то процент (R) определится следующим образом: R = S – P. Процент является одной из форм более общего понятия «экономический эффект», определяемого как разность между результатом и затратами. Декурсивный способ начисления процентов (в конце срока). Введём следующие обозначения: P – величина первоначальной денежной суммы; S – наращенная сумма; i – относительная величина годовой ставки процентов; ic – относительная величина сложной годовой ставки процентов; kн – коэффициент наращения; n - продолжительность периода начисления в годах; q – продолжительность периода начисления в днях; К – продолжительность года в днях. Дата выдачи и дата погашения ссуды всегда считаются за один день. При этом возможны два варианта: - вариант 1: используется точное число дней ссуды и точное число дней в году (365 или 366); - вариант 2: берётся приблизительное число дней ссуды (продолжительность полного месяца принимается равной 30 дням, а продолжительность года 360 дней). Этот метод используется, когда не требуется большая точность, например, при частичном погашении займа. Компаундинг. Простая процентная ставка — это ставка, при которой сумма процента начисляется на первоначально вложенную сумму средств; это означает, что сумма процента, начисленного в предыдущие периоды, не принимается в расчет в процессе последующего наращения. Для простых процентовиспользуются формулы:
Пример 1.Кредит в размере 10 тыс. руб. выдан 5 августа до 14 ноября под 20% годовых, год високосный. Определить размер наращенной суммы для различных вариантов (обыкновенного и точного) расчета процентов. Решение. По условию задачи первоначальная сумма ( Р) равна 10 тыс. руб, относительная величина простой процентной ставки (i) составляет0,2. Наращенную сумму определим по формуле 1. В случае точных процентов берем: август 31-5 = 26 дней, сентябрь - 30 дней; октябрь – 31 день, ноябрь -14 дней. Итого : продолжительность периода начисления процентов составит: q = 26+30+31+14=101 день. 2. Для обыкновенных процентов с приближенным числом дней ссуды: август 31-5 = 26 дней, сентябрь - 30 дней; октябрь – 30 дней, ноябрь -14 дней. Итого : продолжительность периода начисления процентов составит q = 26+30+30+14= 100 дней. S=10 (1+100/360 ∙ 0,20) = 10 ∙ 1,0556 = 10,556 тыс.руб. Ответ:наращенная сумма составит: в случае расчёта точных процентов – 10,552 тыс.руб., для обыкновенных процентов с приближённым числом дней – 10,556 тыс. руб. Пример 2.Кредит в размере 20 тыс.руб. выдается на 2,5 года. Проценты начисляются один раз в конце срока, но ставка процентов за первый год - 30%, а за каждое последующее полугодие она уменьшается на 1%. Определить множитель наращения и наращенную сумму. Решение. По условию задачи первоначальная сумма (Р) равна 20 тыс.руб.; продолжительность периода начисления процентов в годах (n) составляет 2,5 года; относительные величины простых процентных ставок (i) по периодам начисления составят: за два полугодия первого года - i1= 0,3; за первое полугодие второго года - i2=0,29; за второе полугодие второго года - i3=0,28; за первое полугодие третьего года - i4 =0,27. 1. Используем формулу для определения множителя наращения при различных процентных ставках на разных интервалах
2. Используем формулу для определения наращенной суммы при заданном множителе наращения: S = P x kн . S = 20 x 1,72 = 34,4 тыс.руб. Ответ: множитель наращения равен 1,72, а наращенная сумма – 34,4 тыс.руб. Пример 3.Определить период начисления, за который первоначаль-ный капитал в размере 25000 руб. вырастет до 40000 руб., если используется простая ставка 28 процентов годовых. Решение. По условию задачи наращенная сумма (S) составляет 40000 руб., а первоначальная (P) - 25000 руб.; относительная величина простой процентной ставки ( i) составит 0,28. По формуле для определения периода начисления: Ответ: период начисления составит 2,14 года, т.е. 2 года и 2 месяца. Пример 4.Определить простую ставку процентов, при которой первоначальный капитал в размере 24000 руб. достигнет 30000 руб. через год. Решение: По условию задачи величина первоначальной денежной суммы (P) составляет 24000 руб.; наращенной суммы (S) - 30000 руб., продолжительность периода начисления процентов в годах (n) - 1 год. По формуле для определения относительной величины простой процентной ставки Ответ:простая процентная ставка составит 25% годовых. Сложная процентная ставка— это такая ставка, при которой процент начисляется на постоянно нарастающую базу с учетом процентов, начисленных в предыдущие периоды («проценты на проценты»): Для сложных процентов Множитель наращения kн.с. соответственно будет равен kн.с. = (1 + ic)n. Если срок ссуды n в годах не является целым числом, множитель наращения определяют по выражению: kн.с. = (1 + ic)nа (1+ nb ic), где n = nа + nь; nа – целое число лет; nь – оставшаяся дробная часть года. Пример 5.Первоначальная сумма долга (Р) равна 50 тыс.руб. Определить наращенную сумму (S) через 2,5 года по ставке 25% годовых. Решение По формуле S = P ( 1 + ic)na (1 + ic nb) получаем S = 50(1 + 0,25)2 (1 + 0,5∙0,25) = 50∙1,5625∙1,125 =50∙1,7578= 87,89 тыс.руб. Ответ:наращенная сумма составит 87,89 тыс.руб. |



 или
или  где
где  ;
; 

 ; кн = 1 + 0,3 + 0,5 (0,29 + 0,28 + 0,27) = 1,72.
; кн = 1 + 0,3 + 0,5 (0,29 + 0,28 + 0,27) = 1,72. получаем :
получаем :  года.
года.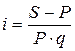 определяем:
определяем: 
