 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Методы формирования долгосрочной финансовой политики предприятия
Эквивалентность процентных ставок различного типа Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые результаты. Обозначения, использованные ранее: i – простая годовая ставка ссудного процента; d – простая годовая учетная ставка; ic – сложная годовая ставка ссудного процента; dc – сложная годовая учетная ставка; Приравнивая попарно формулы для определения наращенной суммы, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками. Приравнивая соотношения – простая годовая ставка ссудного процента – простая годовая учётная ставка Пример 1 Срок уплаты по долговому обязательству – полгода, учетная ставка равна 18%. Какова доходность данной операции, измеренная в виде простой ставки ссудного процента? Решение Используем формулу простой годовой ставки ссудного процента (3.1)
Ответ: простая ставка ссудного процента равна 19,8%.
Пример 2 Кредит выдан на полгода по простой ставке ссудного процента 19,8% годовых. Какова доходность данной операции, приемлемой в виде простой учётной ставки? Решение Используем формулу простой учётной ставки 3.2
Ответ: простая учётная ставка равна 18%.
Из формул – простая годовая ставка ссудного процента – сложная годовая ставка ссудного процента
Пример 3 Первоначальная сумма 300 000 руб. вложена на 2 года с использованием сложной годовой ставки ссудных процентов в размере 16%. Определить эквивалентную простую годовую ставку ссудных процентов. Решение Используем формулу 3.3
Ответ: эквивалентная простая ставка ссудного процента равна 17,28%.
Пример 4 Сумма 300 000 руб. вложена на 2 года с использованием простой годовой ставки ссудных процентов в размере 17,28%. Определить эквивалентную сложную ставку ссудных процентов. Решение Используем формулу 3.4
Ответ: эквивалентная сложная ставка ссудного процента равна 16%. Результаты расчётов в примерах 3 и 4 подтверждают правильность использования формул.
Для различных случаев сложных процентов получаем уравнение эквивалентности, приравнивая формулы: - сложная годовая ставка ссудного процента - номинальная ставка ссудного процента Полученная сложная годовая ставка ссудного процента (ic) эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов. Пример 4а Рассчитать эффективную ставку сложных процентов, если номинальная ставка равна 24% и начисление процентов происходит ежемесячно. Решение Вычисление проводим по формуле
Ответ: эффективная ставка сложных процентов равна 26,8%.
Учет инфляционного обесценения денег в принятии финансовых решений Пусть Sa — сумма, покупательная способность которой с учетом инфляции равна покупательной способности суммы при отсутствии инфляции. Через ΔS обозначим разницу между этими суммами. Отношение ΔS /S, выраженное в процентах, называется уровнем инфляции. При расчетах используют относительную величину уровня инфляции — темп инфляции
Тогда для определения Sa получаем следующее выражение: Sα = S+ ΔS= S+ S Величину (1 + Iи = 1 + Динамика индекса инфляции за несколько лет отражает изменения, происходящие в инфляционных процессах. Понятно, что повышение индекса инфляции за определенный период по сравнению с предыдущим таким же периодом указывает на ускорение инфляции, снижение — на уменьшение ее темпов. Пусть
Разумеется, те же рассуждения применяются, если вместо года берется любой другой временной интервал (квартал, месяц, день и т. д.). Очень важно запомнить данную аналогию со сложным процентом, так как одна из наиболее часто встречающихся ошибок, связанных с расчетом уровня инфляции за некоторый период, связана именно с неучётом данного обстоятельства. Если цены каждый месяц растут на 2%, то за годовой уровень инфляции, недолго думая, принимают 2% • 12 = 24%. Такие расчеты часто используют банки и финансовые компании, привлекая клиентов вкладывать средства, к примеру, под 25% годовых. Между тем, если уровень инфляции составляет 2% в месяц, это значит, что за месяц цены вырастают в (1 + 0,02) = 1,02 раза, а за год— в 1,0212 = 1,268 раза. Значит, годовой темп инфляции составляет 1,268 - 1 = 0,268, т. е. годовой уровень инфляции достигает 26,8%. После такого расчёта процентная ставка 25% годовых теряет свою инвестиционную привлекательность и может рассматриваться лишь в плане минимизации потерь от инфляции.
Пример 5 Цены каждый квартал растут на 3%. Банк привлекает клиентов вкладывать средства по 13% годовых. Требуется определить, покроет ли такая доходность вклада потери от инфляции. Решение 1. Определим индекс инфляции по формуле 3.6
2. Определим темп инфляции используя формулу Iu= 1+ α откуда α = Iu– 1 = 1,1225 – 1 =0,1225 = 12,25%. Ответ: доход от вклада покроет потери от инфляции.
Если в обычном случае первоначальная сумма Р при заданной ставке процентов превращается за определенный период в сумму S, то в условиях инфляции она должна превратиться в сумму Назовем ее ставкой процентов, учитывающей инфляцию. Пусть
d Зададим годовой уровень инфляции
Для данной суммы можно записать еще одно соотношение:
Рассмотрим теперь различные случаи начисления процентов с учетом инфляции. При этом всегда удобно пользоваться значением индекса инфляции за весь рассматриваемый период. Для простых процентных ставок В то же время должно выполняться равенство: Составим уравнение эквивалентности:
Пример 6 При выдаче кредита в сумме 40 млн.руб. должна быть обеспечена реальная доходность операции, определяемая простой процентной ставкой 14% годовых. Кредит выдаётся на полгода, за которую индекс инфляции составит 1,06. Рассчитать значение процентной ставки, компенсирующей потери от инфляции, и наращенную сумму. Решение По условию задачи Р=40 млн.руб., n = 0,5 года, I =0,14, Iu= 1,06. 1. По формуле 3.9 определим процентную ставку, компенсирующую потери от инфляции 2. По формуле 3.7 определим наращенную сумму
3. Наращенную сумму можно определить и по формуле 3.8
Результаты определения наращенной суммы совпадают. Для случая сложных процентов для составления уравнения эквивалентности используем формулы: Отсюда Пример 7 Первоначальный капитал в размере 20 000 руб. выдается на три года, проценты начисляются в конце каждого года по ставке 8% годовых. Определить наращенную сумму с учетом инфляции, если ожидаемый годовой уровень инфляции составляет 12%. Решение По условию задачи Р = 20 000 руб.; n = 3 года; ic= 0,08; α = 0,12. 1. Для определения индекса инфляции воспользуемся формулой 3.7
2. По формуле 3.8 определим наращенную сумму
Ответ: наращенная сумма с учётом инфляции составит 35395 руб.
Вопросы для самопроверки 1. Сформулируйте понятие финансовая политика предприятия. 2. Назовите основные типы задач, решаемых финансовой политикой. 3. В чём состоят отличия управленческого подхода к классификации видов финансовой политики от бухгалтерского подхода? 4. Назовите типы целей деятельности предприятия. 5. Сформулируйте более правильный способ выбора лучшего варианта финансовой политики предприятия. 6. Дайте определение эквивалентной процентной ставки. 7. Что означает понятие «простая годовая процентная ставка эквивалентная простой годовой учётной ставке»? 8. Какая ставка сложных процентов называется «эффективной»? 9. Чем различаются понятия «темп инфляции» и «индекс инфляции»? 10. Чему равен индекс инфляции за год, если цены за каждые полгода растут на 10% ?
[1] Когденко Вера Геннадьевна Краткосрочная и долгосрочная финансовая политика. –М.: ЮНИТИ-ДАНА, 2010.
|



 и
и  , получим:
, получим: (3.1)
(3.1) (3.2)
(3.2)

 можем получить эквивалентные ставки простой и сложной годовой ставки ссудного процента:
можем получить эквивалентные ставки простой и сложной годовой ставки ссудного процента: (3.3)
(3.3)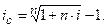 (3.4)
(3.4)






 .
.
 будет больше суммы
будет больше суммы 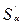 в (1 +
в (1 +  будет больше суммы S'a в (1 +
будет больше суммы S'a в (1 +  вырастет по отношению к сумме S в (1 +
вырастет по отношению к сумме S в (1 +  . (3.6)
. (3.6)
 , что требует уже иной процентной ставки.
, что требует уже иной процентной ставки. – ставка ссудного процента, учитывающая инфляцию;
– ставка ссудного процента, учитывающая инфляцию; – учетная ставка, учитывающая инфляцию.
– учетная ставка, учитывающая инфляцию. (3.7)
(3.7) (3.8)
(3.8)
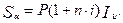
 из которого получаем
из которого получаем (3.9)
(3.9)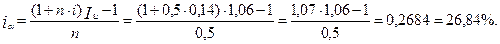
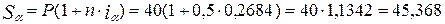 млн.руб.
млн.руб. млн.руб.
млн.руб. и
и 
 (3.10)
(3.10) руб.
руб.