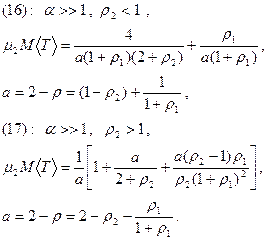ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Интеграция на основе стратегии подвижной границы.

СРС 13 по дисциплине “Теория распределение информации»

Наименование темы: Интеграция на основе стратегии подвижной границы.

Интеграция на основе стратегии подвижной границы.

При этом методе интеграции N канальных интервалов делятся на две части. Одна часть, содержащая N₁ канальных интервалов, предназначается для обслуживания нагрузки первого класса (запросов на соединение). Другая часть, содержащая N₂=N-N₁ канальных интервалов, резервируется для пакетов – обслуживания нагрузки второго класса. Пакеты могут занимать также любой из N₁ канальных интервалов первого класса, если он не используется в данный момент времени. Однако при поступлении заявки первого класса она имеет абсолютный приоритет перед нагрузкой второго класса и сбрасывает при необходимости пакет, занимающий один из N₁ канальных интервалов. В этом и состоит смысл подвижной границы между группами каналов, отведенных для двух различных классов нагрузки. На рис. 1 приведена иллюстрация этого метода.

Рис. 1 Стратегия подвижной границы.

Очевидно, что вероятность блокировки для нагрузки первого класса при такой стратегии предоставления ресурса определяется по В - формуле Эрланга для N₁ серверов. Задержка для пакетов при этом будет не хуже, чем рассчитанная для системы с N₂ серверами, а лучше, поскольку вся оставшаяся от обслуживания нагрузки первого класса пропускная способность системы будет также использоваться для обслуживания пакетов. В системе такого типа также может возникнуть перегрузка для нагрузки второго класса. Максимально допустимая величина этой нагрузки не должна превышать

Здесь вероятность блокировки для нагрузки первого класса определяется по В - формуле Эрланга. Записанное соотношение может быть интерпретировано как интуитивно очевидное, поскольку выражает собой условие не превышать единицу для среднего на один сервер коэффициента использования по отношению к нагрузке второго класса

В знаменателе при этом находится выражение описывающее среднее число каналов, доступных для очереди пакетов. С другой стороны, оно может быть переписано в виде условия ограничения величиной N полной средней нагрузки на систему

Общий анализ системы с подвижной границей оказывается слишком сложным с алгебраической точки зрения. Поэтому при аналитическом исследовании применяются приближенные методы. Раздельно изучаются два возможных режима – не перегруженный (ρ₂<N₂) и режим перегрузки при нарушении этого неравенства. Мы далее построим точное решение задачи с подвижной границей, но только для случая, когда N=2. При этом для реализации стратегии существует единственная возможность выделения под нагрузку первого класса N₁=1 один канальный интервал. Тогда пакеты будут получать один канальный интервал в любом случае, и два, если заявка на соединение будет отсутствовать. Поступление такой заявки немедленно будет снимать один из пакетов с обслуживания, и ставить в общую очередь из заявок второго класса.

Рис. 2 Диаграмма состояний системы с подвижной границей; N=2 канала; N₁=N₂=1 канал.

Рассмотрим диаграмму состояний для такой системы (Рис. 5.5). Пространство состояний для нее также двумерное и состояния могут быть разделены на два яруса, соответствующих случаям i=0 - соединение не установлено и i=1 соединение установлено. В последнем случае диаграмма состояний полностью соответствует системе M/M/1, поскольку один канальный интервал из двух занят под нагрузку первого класса, а второй используется как обычная система с ожиданием. При i=0 имеем диаграмму, соответствующую модели M/M/2, поскольку в случае, когда отсутствует нагрузка первого класса все канальные интервалы (а их у нас два) обслуживают пакетную нагрузку. Переходы между ярусами происходят при поступлении заявки на соединение с интенсивностью l₁ , которое переключает систему обслуживания пакетов с двухлинейной на однолинейную, или при завершении соединения с интенсивностью m₁ , которое производит обратное переключение. Выпишем пять уравнений равновесия для рассматриваемой системы.

Для нахождения решения построенной системы уравнений требуется еще два уравнения. Одно из них это условие нормировки всех вероятностей, а в качестве еще одного будет использовано свойство корней многочлена знаменателя одной из производящих функций.

Определим две производящие функции

Умножая полученное уравнение (11) на z^j и суммируя по всем значениям j>0, преобразуем это уравнение в алгебраическое относительно производящих функций. Повторяя ту же процедуру с уравнением (12) и исключая неизвестные составляющие с помощью (13), (14). Получим в итоге :

Полученные уравнения позволяют сразу выписать несколько важных соотношений, приводящих к определению вероятности блокировки нагрузки первого класса:

Это соотношение в точности соответствует В-формуле Эрланга для однолинейной системы.

Теперь перейдем к определению среднего времени задержки пакетов. Складывая уравнения для производящих функций, сокращая общий множитель правой и левой частях (1-z) и обозначив отношение l₂/m₂=r₂, найдем следующее соотношение

Введем несколько обозначений

Тогда можно найти в явном виде выражения для вероятностей

Выпишем теперь выражения для производящих функций

Найдем соотношение для среднего числа пакетов в системе, исходя из формулы для производящих функций

В качестве подтверждающих правдоподобность полученного выражения соотношений найдем предел правой части при стремлении к нулю нагрузки первого класса и предел при стремлении этой нагрузки к бесконечности.

В первом случае результат в точности соответствует модели M/M/2, а во втором - модели M/M/1 , что и соответствует нашим представлениям.

Воспользовавшись формулой Литтла, выпишем выражение для нормированной задержки в системе

Это выражение еще не является окончательным, поскольку содержит три вероятности, связанные только двумя уравнениями. Как уже было отмечено, воспользуемся некоторыми свойствами корней знаменателя выражения для производящей функции G₀(z). Обратимся к выписанному выше выражению для этой функции.

Пусть z₀ - корень многочлена D₀. Из определения производящей функции необходимо выполнение требования

При этом значении z выражение для числителя также должно обратиться в ноль. Полученное при этом выражение N₀(z₀)=0 и определяет третье необходимое уравнение для нахождения всех вероятностей, входящих в выражение для задержки. Решение алгебраического уравнения третьей степени в общем случае не дается в виде конечной формулы. Мы используем приближенное решение этого уравнения для нахождения двух различных формул для определения задержки пакетов в системе с подвижной границей

На рис.3 приведены графики функции нормированной задержки при различных значениях нагрузки первого класса. Для сравнения приведен график задержки для системы с фиксированным разделением каналов для двух классов нагрузки (по одному каналу на каждый). Как видно из сравнения стратегия подвижной нагрузки дает существенный выигрыш в характеристиках качества обслуживания по сравнению с другими способами интеграции каналов. Анализ показывает, что такое преимущество только усиливается при увеличении числа канальных ресурсов.

Рис.3 Сравнение систем с подвижной и фиксированной границей; N=2; N₁=N₂=1.
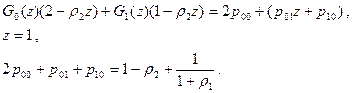