 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Критерии оценивания практических работ 12
Пояснительная записка Методические указания к практическим работам по дисциплине «Теория вероятностей и математическая статистика» предназначены для студентов по специальности 09.02.01 Компьютерные системы и комплексы. Цель методических указаний: оказание помощи студентам в выполнении практических работ по дисциплине «Теория вероятностей и математическая статистика». Настоящие методические указания содержат практические работы, которые позволят студентам закрепить теорию по наиболее сложным разделам дисциплины и направлены на формирование следующих компетенций: ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес. ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития. ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности. ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями. ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий. ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации. ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности. ПК 1.1. Разрабатывать схемы цифровых устройств на основе интегральных схем разной степени интеграции. ПК 1.2. Выполнять требования технического задания на проектирование цифровых устройств. ПК 1.4. Определять показатели надежности и качества проектируемых цифровых устройств. ПК 2.3. Осуществлять установку и конфигурирование персональных компьютеров и подключение периферийных устройств. ПК 3.3. Принимать участие в отладке и технических испытаниях компьютерных систем и комплексов; инсталляции, конфигурировании программного обеспечения. В результате выполнения практических работ по дисциплине «Теория вероятностей и математическая статистика» студенты должны: знать: - основы теории вероятностей; - основы математической статистики. уметь: - вычислять вероятность событий с использованием элементов комбинаторики; - использовать методы математической статистики. Описание каждой практической работы содержит: тему, цели работы, порядок выполнения работы, а так же перечень контрольных вопросов. Для получения дополнительной, более подробной информации по изучаемым вопросам, приведено учебно-методическое и информационное обеспечение.
Практическая работа № 1 Цель: Научиться решать комбинаторные задачи и уравнения. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ В комбинаторике используется в основном три понятия: перестановки, сочетания, размещения. Перестановкаминазывают комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Размещениями называют комбинации, составленные из n различных элементов по k элементов, которые отличаются либо составом элементов, либо их порядком. Сочетаниями называют комбинации, составленные из n различных элементов по k элементов, которые отличаются хотя бы одним элементом. В таблице №1 представлены основные формулы комбинаторики (без повторений). Таблица 1
Существуют два основных правила применяемых при решении комбинаторных задач. Правило суммы. (“или”=”+”) Если некоторый объект А может быть выбран из некоторой совокупности объектов m способами, а объект В может быть выбран n способами, то выбрать либо А, либо В можно выбрать m+n способами. Правило произведения. (“и”=”×”) Если объект А можно выбрать из некоторой совокупности m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов А и В в указанном порядке может быть выбрана m·n способами. ВАРИАНТЫ
ЗАДАНИЯ Задание 1. 1. А) Сколькими способами 6 человек могут сесть на 6 стульев? Б) Сколькими способами в карточке лотереи «Спортлото» можно зачеркнуть 5 номеров из 36? В) В кабину лифта девятиэтажного дома вошли три пассажира, каждый из них может выйти на любом из восьми этажей. Сколько способов разгрузки лифта, при которых на каждом этаже выходит не более одного пассажира. 2. А) Сколькими способами можно составить трехцветный полосатый флаг, если имеются ткани пяти различных цветов? Решите эту задачу при условии, что одно полоса должна красной. Б) Сколькими способами можно составить список из 25 студентов. В) Сколькими способами можно составить команду из 4 человек для соревнования по бегу, если имеется 7 бегунов? 3. А) В цехе работают 8 токарей. Сколькими способами можно поручить трем из них изготовление различных видов деталей (по одному виду на каждого)? Б) Сколькими способами можно поставить 8 шашек на черные поля доски? В) Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов? 4. А) Сколькими способами можно расположить в турнирной таблице 10 футбольных команд, если известно, что никакие две команды не набрали поровну очков? Б) Сколькими способами можно заполнить карточки "Спортлото" (6 номеров из 49)? В) Сколькими способами можно опустить 5 писем в 11 почтовых ящиков, если в каждый из них опускают не более одного письма? 5. А) Сколькими способами можно выбрать двух дежурных из класса, в котором 25 учеников? Б) Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, если цифры в числе не повторяются? В) Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, если номер состоит из одной буквы латинского алфавита (26 букв), за которой следуют четыре цифры, отличные от нуля? 6. А) Сколько нечетных и сколько четных четырехзначных чисел можно составить из цифр числа 3694, если каждую цифру надо использовать один раз? Б) Замок на подъезде имеет 10 кнопок и открывается одновременным нажатием на определенные 3 кнопки. С какой попытки (в худшем случае) можно открыть такой замок? В) Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец? 7. А) В первенстве страны по футболу участвовали 16 команд. Перед началом первенства был объявлен конкурс знатоков, в котором требовалось предсказать распределение медалей. Сколько различных ответов можно дать на этот вопрос? Б) Из состава конференции, на которой присутствуют 52 человека, надо избрать делегацию, состоящую из 5 человек. Сколькими способами это можно сделать? В) На званый вечер приглашены 5 мужчин и 5 женщин. Напротив каждого места на стол необходимо поставить табличку с именем того, кто будет на этом месте сидеть, но никакие два лица одного пола не должны сидеть рядом. Сколькими способами можно расставить таблички? 8. А) У одного человека 7 книг по математике, а у второго – 9. Сколькими способами они могут обменять друг у друга две книги на две книги. Б) Сколько слов можно образовать из букв слова фрагмент, если слова должны состоять из восьми букв? В) Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост! 9. А) Сколькими способами можно расставить на полке семь книг, если две определенные книги должны всегда стоять рядом? Б) При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать? В) Сколько слов можно образовать из букв слова фрагмент, если слова должны состоять из семи букв? 10. А) Сколькими способами можно отобрать два различных фрукта из семи яблок и девяти апельсинов? Б) Сколькими способами можно разместить 3 пассажиров в купе? В) Сколько существует различных автомобильных номеров, которые состоят из пяти цифр? Задание 2. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Ознакомиться с теоретическими сведениями. 2. Выбрать свой вариант задания. 3. Записать исходные данные в тетрадь. 4. Решить задания. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что такое факториал? 2. Что такое перестановки, размещение и сочетание? 3. Формулы перестановки, размещение и сочетание.
Практическая работа № 2 Цель: Научиться раскладывать бином и находить его члены. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Число 1) 2) 3) 4) Последнее равенство следует из свойства 3) при a = b = 1. Равенство 3) называется биномом Ньютона, поэтому Свойство 2) означает, что коэффициенты По следующей формуле находится k + 1 член бинома:. Равенство 2) называется соотношением Паскаля. На этом свойстве основан треугольник Паскаля, изображенный ниже. С С
С \ + \ + \ 1 2 1 С \ + \ + \ + 1 3 3 1 С ‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡‡ 1 4 6 4 1 ВАРИАНТЫ
ЗАДАНИЯ Задание 1. Найдите разложение степени бинома. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Задание 2. Найдите: 1. четвертый член разложения 2. девятый член разложения 3. шестой член разложения 4. четвертый член разложения 5. пятый член разложения 6. седьмой член разложения 7. третий член разложения 8. восьмой член разложения 9. шестой член разложения 10. седьмой член разложения ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Ознакомиться с теоретическими сведениями. 2. Выбрать свой вариант задания. 3. Записать исходные данные в тетрадь. 4. Решить задания. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что такое бином Ньютона? 2. Треугольник паскаля, биномиальные коэффициенты. 3. Свойства биномиальных коэффициентов? 4. Общий член разложения бинома. Практическая работа № 3 Цель: Решение задач с помощью классического определения вероятности. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Испытанием называется осуществление определенной совокупности условий какого-либо эксперимента, наблюдения, которые могут производиться неограниченное число раз. При этом эксперимент и наблюдения включают в себя случайные факторы, влияние которых в каждом испытании приводит к неоднозначности исхода испытания. Событиями называются возможные исходы испытаний (обозначаются А, В, С,...). На основе различных признаков события можно классифицировать следующим образом: по возможности появления: · достоверные; · невозможные; · случайные; по совместности появления: · совместные (происходят одновременно); · несовместные (происходят не одновременно); по взаимозависимости: · зависимыми называются события, при которых вероятность появления одного из них изменяет вероятность появления другого; · независимыми называются события, при которых вероятность появления одного из них не изменяет вероятность появления другого; по сложности: · элементарные события - возможные, исключающие друг друга результаты одного испытания; · сложные события, состоящие из других событий. События образуют полную группу, если в результате испытания появляется хотя бы одно из них. Противоположными называются два несовместных события ( Элементарным событием называется конкретный результат испытания. В результате испытания происходят только элементарные события. Пространством элементарных событий называется совокупность всех возможных, различных, конкретных исходов испытаний. Вероятностью события А называется число равное отношению числа исходов m, благоприятствующих появлению события, к числу всех равновозможных исходов n, образующих полную группу:
Определение вероятности впервые было дано Полем Лапласом и является классическим определением вероятности. Свойства вероятности события: 1. 2. Если А - событие невозможное, то 3. Если В - событие достоверное, то ВАРИАНТЫ
ЗАДАНИЯ Задание 1. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5. Задание 2. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь окрашенных граней: а) одну; б) две; в) три. Задание 3. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую наудачу извлеченную кость можно приставить к первой, если первая кость: а) оказалась дублем; б) не есть дубль. Задание 4. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных в одну линию кубиков можно будет прочесть слово «спорт». Задание 5. На каждой из шести одинаковых карточек напечатана одна из следующих букв: а, т, м, р, с, о. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вынутых по одной и расположенных «в одну линию» карточках можно будет прочесть слово «трос». Задание 6. В замке на общей оси пять дисков. Каждый диск разделен на шесть секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть. Задание 7. Восемь различных книг расставляются наудачу на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом. Задание 8. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры. Задание 9. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных. Задание 10. В урне находится по шесть шаров четырех разных цветов. Найдите вероятность того, что из четырех наугад вытянутых шаров все четыре шара окажутся разных цветов. Задание 11. Какая вероятность того, что наугад выбранное двузначное число, которое делиться на 4, делится и на 12. Задание 12. Какая вероятность того, что наугад выбранное число от 1 до 30 является делителем числа 30. Задание 13. Пусть год имеет 366 дней. Найти вероятность того, что на случайно вырванном листе календаря число: а) кратное 13; б) равно 29. Задание 14. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что на ней окажется всего: а) 2 очка; б) 5 очков; в) 12 очков. Задание 15. Девочка хотела нанизать на нитку 7 различных бусин. Это сделал её братик. Какова вероятность того, что он сделал именно так, как хотела девочка? Задание 16. Из букв, написанных на отдельных карточках, составили слово МАТЕМАТИКА, потом эти карточки перевернули, перетасовали и взяли наугад одну из них. Какова вероятность того, что на ней окажется буква А? Задание 17. В корзине есть 20 яблок, одинаковых на вид, 15 из них – сладкие, а 5 – кислые. Какова вероятность того, что взятые наугад два яблока окажутся кислыми? Задание 18. Из 10 металлических конструкций две – высокого качества. Найдите вероятность того, что среди взятых наугад пяти конструкций только одна – высокого качества. Задание 19. В кульке есть 20 свёрнутых бумажек. На двух из них написано «нет», а на остальных – «да». Какова вероятность того, что на двух взятых наугад бумажках окажется слово «да»? Задание 20. Столовая на обед приготовила 3 первых блюда: борщ, суп, щи; 4 вторых: вареники, голубцы, котлеты, рагу; и 2 десертных: мороженое и пирожное. Какова вероятность того, что кто-нибудь, закажет борщ, котлеты и мороженое? ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Ознакомиться с теоретическими сведениями. 2. Выбрать свой вариант задания. 3. Записать исходные данные в тетрадь. 4. Решить задания. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Основные понятия теории вероятностей (событие, испытание). 2. Классификацию событий на случайные, возможные, совместные, противоположные. 3. Случайные события и операции над ними. 4. Классическое определение вероятности.
Практическая работа № 4 Цель: Решения задач с помощью теорем суммы и произведения вероятностей. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Суммой или объединением двух событий А и В (С = А + В) называется событие С, состоящее в появлении хотя бы одного из них. Теорема сложения вероятностей. Вероятность наступления одного из двух несовместных событий равна сумме их вероятностей, то есть:
Следствие 1. Если события А, В, С образуют полную группу, то сумма их вероятностей равна 1. Следствие 2. Сумма вероятностей двух противоположных событий А и А̅ равна 1. Произведением или пересечением событий А и В называется событие С (С = А × В), состоящее в совместном наступлении этих событий, то есть в наступлении события А и события В. Два случайных события А и В называются зависимыми, если наступление одного из них изменяет вероятность наступления другого. Условной вероятностью события В называется вероятность наступления события В при условии, что событие А уже наступило. Обозначается: P(B/A) или PA(В). Теорема умножения вероятностей. Вероятность совместного наступления событий А и В, равна произведению вероятности одного из них на условную вероятность другого:
Следствие. Вероятность произведения двух независимых событий равна произведению их вероятностей:
Теорема сложения вероятностей для случая, когда события совместны. Вероятность наступления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий, минус вероятность их совместного появления, то есть
Есть задачи когда «хотя бы» одно из событий должно произойти и да бы не перебирать все возможные комбинации рационально построить решение от обратного, то есть от вероятности полной группы событий вычесть вероятность невозможного события:
ВАРИАНТЫ
ЗАДАНИЯ Задание 1. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. Задание 2. В денежно-вещевой лотерее на каждые 10 000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета? Задание 3. Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1; вероятность выбить 9 очков 0,3; вероятность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков. Задание 4. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2 деталей есть хотя бы одна стандартная. Задание 5. В ящике 10 деталей, среди которых 2 нестандартных. Найти вероятность того, что в наудачу отобранных 6 деталях окажется не более одной нестандартной. Задание6. Из 10 карточек, содержащих цифры от 0 до 9, наугад выбирают две. Какова вероятность того, что цифры на выбранных карточках будут отличаться друг от друга не более чем на две единицы. Задание 7. В урне находится по шесть шаров четырех разных цветов. Найдите вероятность того, что из четырех наугад вытянутых шаров все четыре шара окажутся одного цвета. Задание 8. В лотерее из 20 билетов 5 билетов с выигрышем 100 грн. и 5 билетов с выигрышем 50 грн. Какова вероятность того, что при покупке двух лотерейных билетов выигрыш составит: а) не менее 100 грн.; б) ровно 100 грн.? Задание 9. По статистическим данным ремонтной мастерской, в среднем на 20 остановок токарного станка приходится: 10 – для смены резца; 3 – из-за неисправности привода; 2 – из-за несвоевременной подачи заготовок. Остальные остановки проис-ходят по другим причинам. Найти вероятность остановки станка по другим причинам. Задание 10. В корзине 5 белых и 7 черных перчаток. Найти вероятность того, что пара, которую достали наугад, окажется одноцветной. Задание 11. Монета подбрасывается дважды. Найдите вероятность того, что при этом герб выпадет два раза. Задание 12. Игральная кость бросается дважды. Какова вероятность того, что при этом два раза выпадет одно и то же число? Задание 13. Вероятность того, что стрелок при одном выстреле попадает в мишень, равна 0,9. Стрелок произвел 3 выстрела. Найти вероятность того, что все 3 выстрела дали попадание. Задание 14. Три стрелка поражают цель с одного выстрела с вероятностью 0,7; 0,6; 0,4 соответственно. Все стрелки сделали по одному выстрелу по одной и той же цели. Найдите вероятность того, что цель поражена. Задание 15. Предприятие изготовляет 95% изделий стандартных, причем из них 86% – первого сорта. Найти вероятность того, что взятое наудачу изделие, изготовленное на этом предприятии, окажется первого сорта. Задание 16. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков – конусный, а второй – эллиптический. Задание 17. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар, при втором – черный и при третьем – синий. Задание 18. Имеется 3 ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными. Задание 19. В двух ящиках находятся детали: в первом – 10 (из них 3 стандартных), во втором – 15 (из них 6 стандартных). Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными. Задание 20. Вероятность поражения цели первым стрелком при одном выстреле равна 0,8, а вторым стрелком – 0,6. Найти вероятность того, что цель будет поражена только одним стрелком. Задание 21. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: 0,7; 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий. Задание 22. Из колоды в 36 карт наудачу вынимается одна. Какова вероятность того, что будет вынута пика или туз. Задание 23. В типографии имеется 2 плоскопечатные машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина. Задание 24. В студии телевидения 2 телевизионные камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера. Задание 25. Чему равна вероятность того, что при бросании двух игральных костей 6 очков появится хотя бы на одной из костей? Задание 26. С первого предприятия поступило 200 пробирок, из которых 190 стандартных, а со второго – 300, из которых 280 стандартных. Найти вероятность того, что наудачу взятая пробирка будет стандартной. Задание 27. Вероятность поражения цели первым стрелком при одном выстреле равна 0,8, а вторым стрелком – 0,6. Найти вероятность того, что цель будет поражена только одним стрелком. Задание 28. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0,7, а вторым – 0,6. Найти вероятность того, что хотя бы один из стрелков попал в мишень. Задание 29. Из 30 учащихся школы 12 человек занимаются баскетболом, 15 – волейболом, 5 – волейболом и баскетболом. Какова вероятность того, что наугад выбранный учащийся будет заниматься только волейболом или только баскетболом? Задание 30. В большой популяции дрозофил 25% мух имеет мутацию глаз, 50% – мутацию крыльев, а 40% с мутацией глаз имеют и мутацию крыльев. Какова вероятность того, что у мухи, наудачу выбранной из этой популяции, окажется хотя бы одна из этих мутаций? ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Ознакомиться с теоретическими сведениями. 2. Выбрать свой вариант задания. 3. Записать исходные данные в тетрадь. 4. Решить задания. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Классификацию событий на случайные, возможные, совместные, противоположные. 2. Случайные события и операции над ними. Классическое определение вероятности. 3. Теоремы сложения и умножения вероятностей. Независимость событий. Условная вероятность.
Практическая работа № 5 Цель: Решения задач с помощью формулы полной вероятности и Байеса. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Объединение теорем сложения и умножения выражается в формуле полной вероятности. Теорема. Вероятность события А, которое может произойти при осуществлении одного из несовместных событий H1, H2 , H3 ,..., Hn , образующих полную группу, определяется формулой:
Замечание. События H1, H2 , H3 ,..., Hn называются гипотезами. При решении практических задач, когда событие А, появляющееся совместно с каким-либо из несовместных событий H1, H2 , H3 ,..., Hn, образующих полную группу, произошло и требуется произвести количественную переоценку вероятностей событий H1, H2 , H3 ,..., Hn применяются формулы Бейеса (Bayes):
ВАРИАНТЫ
ЗАДАНИЯ Задание 1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго – 0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная. Ответ: 0,85. Задание 2. В телевизионном ателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы. Ответ: 0,875. Задание 3. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника – 0,9, для велосипедиста – 0,8 и для бегуна – 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму. Ответ: 0,86. Задание 4. На сборку поступает 100 деталей с первого станка, 150 деталей со второго станка и 150 деталей с третьего станка. Вероятность появления бракованной детали с первого станка – 0,01, со второго – 0,02, с третьего – 0,01. Найдите вероятность того, что наугад взятая со сборочного конвейера деталь не будет бракованной. Ответ: 0,98625. Задание 5. Вероятность появления бракованной детали при поступлении изделий с первого завода составляет 0,005, а при поступлении изделий со второго завода – 0,008. Найдите вероятность появления бракованной детали в партии, содержащей 1200 деталей с первого завода и 1800 деталей со второго завода. Ответ: 0,0068. Задание 6. Сборщик получил 3 коробки деталей, изготовленных заводом № 1, и 2 коробки деталей, изготовленных заводом № 2. Вероятность того, что деталь завода № 1 стандартна, равна 0,8, а завода № 2 – 0,9, Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь. Ответ: 0,84. Задание 7. В первом ящике содержится 20 деталей, из них 15 стандартных; во втором – 30 деталей, из них 24 стандартных; в третьем – 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика – стандартная. Ответ: 43/60. Задание 8. В первой коробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке – 10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной. Ответ: 0,9. Задание 9. В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1 нестандартная; во втором 10 ламп, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной. Ответ: 13/132. Задание 10. Три станка производят соответственно 50%, 30% и 20% всех изделий. В их продукции брак составляет соответственно 1%, 2% и 1,5%. Какова вероятность того, что выбранное наугад изделие окажется бракованным? Ответ: 0,014. Задание 11. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер. Ответ: 141/239. Задание 12. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй – 6, из третьей группы – 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент? Ответ: Вероятности того, что выбран студент первой, второй, третьей групп, соответственно равны: 18/59, 21/59, 20/59. Задание 13. Вероятность для изделий некоторого производства удовлетворять стандарту равна 0,96. Предлагается упрощенная система проверки на стандартность, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту, а для изделий, которые не удовлетворяют стандарту, – с вероятностью 0,05. Найти вероятность того, что изделие, признанное при проверке стандартным, действительно удовлетворяет стандарту. Ответ: 0,998. Задание 14. Партия деталей изготовлена тремя рабочими, причем первый рабочий изготовил 25% всех деталей, второй 35%, третий 40%. В продукции первого рабочего брак составляет 5%, второго 4%, третьего 2%. Случайно выбранная деталь для контроля оказалась бракованной. Какова вероятность того, что она изготовлена вторым рабочим? Ответ: 28/69. Задание 15. Предположим, что 5% всех мужчин и 0,25% все женщин дальтоники, а население Земли соотносится как 48% мужчин и 52% женщин. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина? Ответ: 240/253. Задание 16. Имеется два одинаковых ящика с шарами. В первом ящике 2 белых и 1 черный шар, а во втором – 1 белый и 4 черных шара. Наудачу выбирают один ящик и вынимают из него белый шар. Какова вероятность того, что вытянутый шар был в первом ящике? Ответ: 10/13. Задание 17. Два автомата производят одинаковые хирургические зажимы. Производительность первого автомата вдвое больше, чем второго. Первый автомат производит в среднем 60% зажимов отличного качества, а второй – 84%. Наудачу взятый зажим оказался отличного качества. Найти вероятность того, что он произведен первым автоматом. Ответ: 10/17. Задание 18. В двух урнах – 6 зеленых и 4 желтых шара. В двух других урнах – 8 зеленых и 2 желтых шара. В последней урне – 2 зеленых и 8 желтых шаров. Наудачу выбирается урна и из нее извлекается шар, который оказался зеленым. Какова вероятность того, что он из первых двух урн? Ответ: 0,4. Задание 19. На складе хранятся лампы, изготовленные тремя цехами, причем первый цех изготовил 25% всех ламп, второй 50%, третий 25%. Вероятность выйти из строя в течении года для ламп изготовленных в первом цеху составляет 10%, во втором 20%, третьем 40%. Случайно выбранная лампа для контроля оказалась бракованной. Какова вероятность того, что она изготовлена вторым цехом? Ответ: 10/77. Задание 20. Стрельбу в цель ведут 3 солдата. Для первого из них вероятность попадания 0,6, для второго – 0,5 и для третьего – 0,3. Какова вероятность того, что цель поразит второй стрелок? Ответ: 5/14. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Ознакомиться с теоретическими сведениями. 2. Выбрать свой вариант задания. 3. Записать исходные данные в тетрадь. 4. Решить задания. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Случайные события и операции над ними. 2. Классификацию событий на случайные, возможные, совместные, противоположные. 3. Формула полной вероятности. Формулы Байеса.
Практическая работа № 6 Цель: Решения задач с помощью формул Бернулли, Пуассона, Лапласа. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Пусть производится n последовательных независимых испытаний. Результат каждого испытания (события А) будем считать не зависящим от того, какой результат наступил в предыдущих испытаниях. Пусть вероятность P(A) появления события А постоянна и равна p. Вероятность
При n >20 и p<0,1 использование формулы Бернулли затруднительно, в этих случаях для вычисления вероятности появления события А ровно k раз используется формула Пуассона:
где λ = np – среднее число появлений события А в n испытаниях. λ является параметром распределения Пуассона. Значения распределения Пуассона для различных λ и k про табулированы и приводятся в приложении А. При n >20 и p>0,1 использование формулы Бернулли и Пуассона затруднительно, в этих случаях для вычисления вероятности появления события А ровно k раз используется формула Лапласа (локальная теорема Лапласа):
где Функция Вероятность появления события при n испытаниях в интервале от k1 до k2 раз вычисляется по интегральной формуле Лапласа:
где Функция ВАРИАНТЫ
ЗАДАНИЯ Задание 1. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы. Задание 2. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент включено 4 мотора. Задание 3. Найдите вероятность того; что, если подбрасывать монету 10 раз, она упадет гербом вверх 2 раза. Задание 4. Найдите вероятность того, что при пятикратном подбрасывании кубика, на грани которого нанесены цифры от 1 до 6, цифра 3 выпадет 2 раза. Задание 5. Вероятность попадания стрелком в цель при одном выстреле составляет 0,6. Найдите вероятность 6 попаданий из 10 выстрелов. Задание 6. Вероятность появления бракованной детали составляет 0,1. Найдите вероятность того, что среди 10 отобранных деталей одна окажется бракованной. Задание 7. В приборе 4 лампы. Вероятность выхода из строя в течение года для каждой лампы равна 1/6. Какова вероятность того, что в течение года придется заменить не менее половины всех ламп? Задание 8. Вероятность того, что суточный расход газа на предприятии не превысит нормы, равна 0,9. Какова вероятность того, что в течение недели предприятие трижды допустит перерасход газа? Задание 9. Самолет имеет 4 двигателя. Вероятность нормальной работы каждого двигателя равна 0,95. Найти вероятность того, что в полете могут возникнуть неполадки в одном из двигателей. Задание 10. Для нормальной работы на линии должно быть не менее 8 автобусов, а их имеется 10. Вероятность невыхода каждого автобуса на линию равна 0,1. Найти вероятность работы в ближайший день. Задание 11. Известно, что вероятность «зависания» компьютера в интернет-кафе равна 0,6%. Какова вероятность того, что при случайном отборе 200 компьютеров «зависнут» ровно 6 компьютеров? Задание 12. При наборе текста наборщик делает ошибку в слове с вероятностью 0,001. Какова вероятность, что в набранной книге, насчитывающей 5000 слов, будет не более 5 ошибок? Задание 13. Страховая фирма заключила 10000 договоров. Вероятность страхового случая по каждому в течении года составляет 2%. Найти вероятность того, что таких случаев будет не более 250. Задание 14. Сборник задач содержит 400 задач с ответами. В каждом ответе может быть ошибка с вероятностью 0,01. Какова вероятность, что для 99% всех задач сборника ответы даны без ошибок? Задание 15. В партии из 768 арбузов каждый арбуз оказывается неспелым с вероятностью 0,05. Найти вероятность того, что количество спелых арбузов будет 600. Задание 16. Известно, что вероятность выпуска дефектной детали равна 0,02. Детали укладываются в коробки по 100 штук. Чему равна вероятность того, что число дефектных деталей не более двух? Задание 17. В партии 100 изделий, из которых 4 бракованных. Партия разделена на две равные части, которые отправлены двум потребителям. Какова вероятность того, что все бракованные изделия достанутся одному потребителю? Задание 18. По данным технического контроля в среднем 2% изготавливаемых на заводе часов нуждаются в дополнительной регулировке. Какова вероятность того, что из 300 изготовленных часов 20 штук не будут нуждаться в дополнительной регулировке? Задание 19. В коробке 3 детали, вероятность брака для каждой детали равна 0,1. Какова вероятность того, что среди 10 коробок будет не менее 8 не содержащих бракованных деталей? Задание 20. Производители калькуляторов знают из опыта, что 1% проданных калькуляторов имеет дефекты. Аудиторская фирма купила 500 калькуляторов. Какова вероятность того, что придется заменить 4 калькулятора? Задание 21. Вероятность того, что в партии из 100 изделий имеется брак, составляет 63,2%. Найти вероятность, что там не более 3 бракованных изделии. Задание 22. На научную конференцию приглашены 100 человек, причем каждый из них прибывает с вероятностью 0,7. В гостинице для гостей заказано 65 мест. Какова вероятность, что все приезжающие будут поселены в гостинице? Задание 23. Баскетболист бросает мяч три раза. Вероятность попадания при каждом броске равна 0,7. Какова вероятность того, что он попадет один раз? Задание 24. При передаче сообщения вероятность искажения знака равна 0,1. Какова вероятность того, что сообщение из 10 знаков будет содержать 3 искажения? Задание 25. При установившемся технологическом процессе происходит 10 обрывов нити на 100 веретенах в час. Какова вероятность того, что в течение часа на 80 веретенах произойдет 7 обрывов нити? Задание 26. Установлено, что в среднем 0,5% шариков, изготовленных для подшипников, оказываются бракованными. Какова вероятность того, что среди поступивших на контроль 10 000 шариков бракованными окажутся 50 штук? Задание 27. В результате проверки качества приготовленного для посева зерна было установлено, что 90% зерен всхожие. Какова вероятность того, что среди отобранных и высаженных 1000 зерен прорастет не менее 700 штук? Задание 28. Вероятность выпуска нестандартной электролампы равна 0,1. Чему равна вероятность того, что в партии из 2000 ламп число стандартных будет 90 штук? Задание 29. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2. Задание 30. Известно, что вероятность выпуска дефектной детали равна 0,2. Детали укладываются в коробки по 100 штук. Чему равна вероятность того, что в коробке 20 дефектных деталей? ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Ознакомиться с теоретическими сведениями. 2. Выбрать свой вариант задания. 3. Записать исходные данные в тетрадь. 4. Решить задания. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Повторные испытания. 2. Формула Бернулли. 3. Формула Пуассона. 4. Формула Лапласа.
Практическая работа № 7 Цель: Построение законов распределения. Нахождение наивероятнейшего числа появления события. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Случайной величиной называется функция Случайная величина называется дискретной (прерывной), если множество ее возможных значений конечно или счетно. Случайная величина называется непрерывной, если существует неотрицательная функция Например, число студентов на лекции – дискретная случайная величина, а продолжительность лекции - непрерывная случайная величина. Случайные величины обозначаются заглавными буквами латинского алфавита X, Y, Z, а их возможные значения - соответствующими прописными буквами x1, x2,..., xn. Законом распределения случайной величины называется соответствие, устанавливающее связь между возможными значениями случайных величин и их вероятностями. Закон распределения может быть задан: § аналитически; § таблично; § графически. Закон распределения дискретной случайной величины задаётся чаще всего рядом распределения, т.е. таблицей
в которой x1, x2,..., xn – расположенные по возрастанию значения дискретной случайной величины X, а p1, p2, …, pn – соответствующие этим значениям вероятности. То, что случайная величина Х принимает одно из значений х1, х2, … , хn, является достоверным событием и поэтому выполняется равенство Биномиальный закон распределения – это распределение дискретной случайной величины согласно формуле Бернулли Пуассоновский закон распределения – это распределение дискретной случайной величины согласно формуле Пуассона На практике иногда требуется знать найвероятнейшее число наступления события в схеме Бернули, то есть при каком m и фиксированном n вероятность Pn(m) принимает наибольшее значение. Обозначим это наивероятнейшее число через m0 и найдем его, применив формулу Бернулли. Рассмотрим отношение:
В зависимости от значений параметров n, m, p, q возможны три варианта:
Наивероятнейшее число m0 должно удовлетворять условиям:
откуда
то есть найвероятнейшая частота m0 находится в интервале ВАРИАНТЫ
ЗАДАНИЯ Задание 1. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,2. Составить закон распределения числа отказавших элементов в одном опыте. Задание 2. В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать закон распределения дискретной случайной величины X – числа нестандартных деталей среди четырех отобранных. Задание 3. Написать биномиальный закон распределения дискретной случайной величины X – числа появлений «герба» при двух бросаниях монеты. Задание 4. Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X – числа выпадений четного числа очков на двух игральных костях. Задание 5. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны три детали. Составить закон распределения числа стандартных деталей среди отобранных. Задание 6. В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X – числа стандартных деталей среди отобранных. Задание 7. После ответа студента на вопросы экзаменационного билета экзаменатор задает студенту дополнительные вопросы. Преподаватель прекращает задавать дополнительные вопросы, как только студент обнаруживает незнание заданного вопроса. Вероятность того, что студент ответит на любой заданный дополнительный вопрос, равна 0,8. Составить закон распределения случайной дискретной величины X – числа дополнительных вопросов, которые задаст преподаватель студенту. Задание 8. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,8. Стрелку выдаются патроны до тех пор, пока он не промахнется. Составить закон распределения случайной дискретной величины X – числа патронов, выданных стрелку. Задание 9. Баскетболист бросает мяч три раза. Вероятность попадания при каждом броске равна 0,7. Составить закон распределения числа попаданий среди трех бросков. Задание 10. При передаче сообщения вероятность искажения знака равна 0,1. Сообщение состоит из 10 знаков. Составить закон распределения числа искаженных знаков среди 3 отобранных. Задание 11. Производители калькуляторов знают из опыта, что 1% проданных калькуляторов имеет дефекты. Аудиторская фирма купила 500 калькуляторов. Составить закон распределения числа бракованных среди четырех отобранных калькуляторов. Задание 12. Устройство состоит из 1000 элементов, работающих независ 12 |
, где n! = 
– факториал. По определению 0! = 1.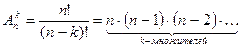
;
;
;
;
;
;
;
;
;
;
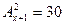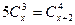обладает следующими свойствами:
;
;
, где 
.
.
С 
в биноме степени n + 1 получаются суммированием двух соседних коэффициентов в биноме n-ой степени.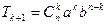
.
С 
1
\ + 1 1
С 
С 
\ +
С 
С 
С 
\ + \ +
С 
С 
С 
С 
\ + \ + \ +
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
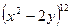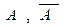), образующих полную группу событий.
.
.
.
.
.
или 
,
.
.
.
.
события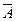 
обозначим через q: 
. В случае небольшого числа испытаний вероятность того, что в n испытаниях это событие наступит ровно k раз рассчитывается по формуле Бернулли:
.
,
,
, 
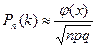. Значения функции 
для различных x про табулированы и приводятся в приложении Б.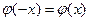
и 
.
,
, 
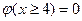для различных x про табулированы и приводятся в приложении В.
нечетная, то есть 
и 
.
, определенная на множестве элементарных событий 
.
такая, что 
.
.
.
.
при 
;
при 
;
при 
.
; 
,
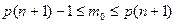. Учитывая, что 
, после преобразований 
имеем
,
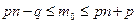, длина которого равна единице. Так как наивероятнейшая частота может выражаться только целым числом, она может принимать или одно значение, если границы выражены дробными числами, или два значения, если гранцы сами являються целыми числами. Тогда нужно вравнить вероятности на концах.