 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Средняя квадратичная и средняя арифметическая ошибки. 12
Для того чтобы выявить случайную ошибку измерений, необходимо повторить измерение несколько раз. Если каждое измерение дает несколько отличные от других измерений результаты, мы имеем дело с ситуацией, когда случайная ошибка играет существенную роль. За наиболее вероятное значение измеряемой величины следует принять её среднее арифметическое значение, вычисленное из всего ряда измеренных значений. Допустим, что сделано N измерений. Разумеется, что они проделаны одним и тем же методом и с одинаковой степенью тщательности. Такие измерения называют равноточными. Для оценки величины случайной ошибки измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или средней квадратичной ошибки. Иногда применяется средняя арифметическая ошибка. Средней квадратичной ошибкой называется величина
Если число наблюдений очень велико, то подверженная случайным колебаниям величина sn стремится к некоторому постоянному значению σ, которое можно назвать статистическим пределом sn: σ=lim sn, при n→∞. Собственно говоря, именно этот предел и называется средней квадратичной ошибкой. Квадрат этой величины называется дисперсией измерений. В действительности мы всегда вычисляем не величину σ, а её приближенное значение sn, которое тем ближе к σ, чем больше n. Относительная величина средней квадратичной ошибки w, выраженная в процентах, носит название коэффициента вариации
Средняя арифметическая ошибка rn вычисляется по формуле Обозначение Точно так же, как и для средней квадратичной ошибки, истинное значение средней арифметической ошибки ρ определяется соотношением ρ = lim rn, при n→∞. Обозначим истинное значение измеряемой величины через x. Её среднее арифметическое значение, полученное в результате измерений Р( Вероятность а носит название доверительной вероятности, или коэффициента надежности. Интервал значений от Это выражение означает, что с вероятностью, равной а, результат измерений не выходит за пределы доверительного интервала от Мы пришли к очень важному заключению: для характеристики величины случайной ошибки необходимо задать два числа, а именно: величину самой ошибки (или доверительного интервала) и величину доверительной вероятности. Знание доверительной вероятности позволяет оценить степень надежности полученного результата. При обычных измерениях можно ограничиться доверительной вероятностью 0,9 или 0,95. Удобство применения стандартной ошибки в качестве основного численного выражения погрешности наблюдений заключается в том, что этой величине соответствует вполне определенная доверительная вероятность, равная 0,68 (2σ→0,95, 3σ→0,997). 12 |



 .
. .
. .
. выражает, что при подсчете все разности считаются положительными, без учета их действительного знака; иначе говоря, суммируются абсолютные значения величин
выражает, что при подсчете все разности считаются положительными, без учета их действительного знака; иначе говоря, суммируются абсолютные значения величин  .
.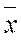 , а погрешность измерения этой величины Δx. Пусть a означает вероятность того, что результат измерений отличается от истинного значения на величину, не большую, чем Δх. Это принято записывать в виде
, а погрешность измерения этой величины Δx. Пусть a означает вероятность того, что результат измерений отличается от истинного значения на величину, не большую, чем Δх. Это принято записывать в виде - Δх < х <
- Δх < х <  + Δх) = а.
+ Δх) = а.