 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вопрос 3. Непараметрические методы оценки корреляционной связи показателей.
На практике часто необходимо точно регистрировать не только количественные, но и качественные факторы. При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, возможно использование "тетрахорических показателей". Расчётная таблица для двух признаков состоит из четырёх ячеек (а,в,с,d). Каждая клетка соответствует альтернативе того и другого признака.
Для анализа данных из таких таблиц построен ряд показателей:
- коэффициент ассоциации Д. Юла Кa : Кa =
- коэффициент контингенции К.Пирсона Кк :
Кк =
Коэффициент контингенции всегда находится в пределах от -1 до +1. Кроме того, значение коэффициента контингенции всегда меньше коэффициента ассоциации. -1 < Кк < +1 ; Кк < Ка .
Применение понятий: Проведен анализ «Исследование социальных аспектов трудовой деятельности работников торговых предприятий». Исследования по полу и содержанию работы представлены в таблице:
Определить по данным таблицы коэффициент ассоциации.
По шкале Чеддока проверим Кa. Вывод: имеет место средний размер связи, несмотря на разные мнения о своей работе у мужчин и женщин.
Для определения тесноты связи как между количественными, так и между качественными признаками (если значения признаков могут быть упорядочены, проранжированы по степени убывания или возрастания признака) можно использовать коэффициент корреляции рангов Спирмена rсп : rсп=1 - где n - число наблюдений (число пар рангов). Применение понятий: Рассмотрим наличие связи между обеспеченностью товарной продукцией ряда предприятий (х) и накладными расходами по реализации (у). Значения х и у приведены в первых двух колонках следующей таблицы:
Определим коэффициент Спирмена.
Необходимые величины для расчёта rсп найдены и записаны в колонках 3...6 таблицы, тогда:
rсп = 1 - 6*50/10*99 = 0,700
Вывод: выявленная связь (по шкале Чеддока) является заметной.
Если каждый качественный признак состоит более чем из двух групп, то для определения тесноты связи применяются: коэффициент взаимной сопряженности К.Пирсона:
Здесь φ2 - показатель взаимной сопряженности.
коэффициент взаимной сопряженности А.А.Чупрова:
Здесь К1 - число групп по колонкам; К2 - число групп по строкам. Коэффициент взаимной сопряженности А.А.Чупрова находится в пределах от 0 до 1. Это более точный коэффициент, по сравнению с коэффициентом взаимной сопряженности К.Пирсона, т.к. учитывает число групп по каждому признаку. 0 < Сr < +1 Чупров Александр Александрович (1874-1926) – русский теоретик статистики. С 1917г. проживал за границей. Если надо найти тесноту связи между тремя и более признаками, то применяется ранговый коэффициент согласия - коэффициент конкордации W: W = где S - сумма квадратов отклонений рангов, m - количество факторов, n - число наблюдений. Применение понятий: Для десяти однотипных совместных предприятий известны следующие показатели:
Рассчитаем тесноту связи между указанными факторами с помощью коэффициента конкордации. Выполняем вспомогательные расчеты, результаты которых представим в таблице. Присваиваем ранги исходным данным:
S = 5590 - (220)2/10 = 5590 - 4840 = 750 W = (12*750) / (16*(1000-10)) = 0,57 Выводы:
Величина коэффициента конкордации показывает, что между исследуемыми величинами имеется тесная зависимость. Это объясняется тем, что все рассматриваемые величины являются показателями эффективности работы СП.
|



 (26)
(26) (27)
(27)
 ,
,  (28)
(28) - квадраты разности рангов связанных величин х и у,
- квадраты разности рангов связанных величин х и у, (29)
(29)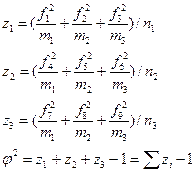 (30)
(30) (31)
(31) ,
,