 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пример вычисления некоторых Z-изображений.
Свойства Z-преобразования 1. Линейность Формулировка. Z-преобразование линейной комбинации последовательностей равно линейной комбинации Z-преобразований отдельных последовательностей, при условии, что они существуют. Ƶ где Доказательство. Ƶ Очевидно, что равенство выполняется при условии сходимости всех рядов, а значит при условии существования Z-образов последовательностей
2. Z-преобразование задержанной копии последовательности Формулировка. Дана последовательность Доказательство. Запишем прямое Z-преобразование для задержанной копии:
Сделаем замену переменных
Здесь учтено, что 3. Z-преобразование дискретного сигнала умноженного на экспоненциальную последовательность. Формулировка. Дана последовательность
Доказательство. Запишем Z-преобразование для сформированной последовательности:
4. Z-преобразование свертки двух последовательностей Формулировка. Последовательность
Доказательство. Запишем Z-преобразование свертки:
Сделаем замену переменных
Таблица.1 Z-изображения типовых последовательностей
Пример вычисления некоторых Z-изображений. Пример 1. Вычислить z-преобразование последовательности
Решение. Запишем выражение для Z-преобразование последовательности :
Очевидно, что Z-изображение является суммой геометрической прогрессии с начальным значением
Используя выражение для суммы бесконечно убывающей геометрической прогрессии, найдем z-изображение в форме:
В последнем равенстве числитель и знаменатель дроби были умножены на z.
Пример 2. Вычислить z-преобразование последовательности
Решение 1. Запишем выражение для Z-преобразование последовательности :
Очевидно, что Z-изображение является суммой геометрической прогрессии с начальным значением
Используя выражение для суммы бесконечно убывающей геометрической прогрессии, найдем z-изображение в форме:
В последнем равенстве числитель и знаменатель дроби были умножены на z.
Решение 2. Воспользуемся свойством умножения сигнала на экспоненциальную последовательность.
Рассмотрим последовательность из примера 1. Ее изображение нам известно в форме . Последовательность может быть сформирована из последовательности с помощью выражения:
где
Воспользуемся выражением для
Пример 3. Вычислить z-преобразование последовательности
Решение. Очевидно, что
Учитывая линейность операций суммирования и дифференцирования, получим
Пример 4. Вычислить z-преобразование последовательности
Решение.
Полагая в и
Примечание. Z-изображения последовательностей № 3-15 из таблицы 1 можно получить из Z-изображения единичного скачка (№2) с использованием свойства умножения сигнала на экспоненциальную последовательность, свойства линейности z-преобразования и с помощью операции дифференцирования по параметру
Примечание 2. Z-изображения типовых дискретных сигналов описываются дробно-рациональными функциями, т.е. функциями являющимися отношением двух полиномов переменной z. В этом смысле Z-изображения типовых дискретных сигналов аналогичны изображениям по Лапласу типовых непрерывных сигналов.
Примеры использования теоремы Коши о вычетах для нахождения обратного z-преобразования.
Обратное Z-преобразование определяется выражением:
где В соответствии с теоремой Коши о вычетах искомая последовательность может быть найдена в виду суммы вычетов во всех полюсах подынтегрального выражения:
где Z-изображения
является произведением дробно-рациональных функций и, как следствие, само имеет дробно-рациональную форму. Тогда подынтегральное выражение в можно представить в форме
где С учетом , формула для вычисления вычета в полюсе
Для простого полюса
Пример 5. Вычислить обратное z-преобразование от изображения Решение.
Подынтегральное выражение в имеет вид:
Изображение имеет два простых полюса
где
Тогда
Пример 6. Вычислить обратное z-преобразование от изображения Подынтегральное выражение в имеет вид:
Изображение имеет один полюс третьего порядка
Пример 7. Вычислить обратное z-преобразование от изображения Подынтегральное выражение в примет вид:
Изображение имеет два простых полюса
где
Тогда |




 Ƶ
Ƶ  +
+  Ƶ
Ƶ  =
=  ,
, и
и  – константы, в общем случае комплексные.
– константы, в общем случае комплексные.
 и
и  по-отдельности. Может возникнуть ситуация, когда ряд для линейной комбинации двух последовательностей сходится за счет сбалансированности противофазных членов при определенном подборе коэффициентов
по-отдельности. Может возникнуть ситуация, когда ряд для линейной комбинации двух последовательностей сходится за счет сбалансированности противофазных членов при определенном подборе коэффициентов  . Z-изображение
. Z-изображение  задержанной на m отсчетов копии данной последовательности
задержанной на m отсчетов копии данной последовательности  равно
равно  .
. .
. , тогда:
, тогда:
 и
и  при
при 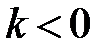 .
. , где
, где  – некоторая постоянная. Тогда Z-изображение сформированной последовательности равно
– некоторая постоянная. Тогда Z-изображение сформированной последовательности равно  .
. .
.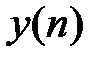 является результатом дискретной свертки двух последовательностей
является результатом дискретной свертки двух последовательностей  и
и  , Z-изображения
, Z-изображения  . Z-изображение последовательности
. Z-изображение последовательности 


 , тогда
, тогда В последнем равенстве было учтено, что
В последнем равенстве было учтено, что  для
для  (физически реализуемые системы). Можно показать, что свойство справедливо, если обе последовательности отличны от нуля в области отрицательных времен и имеют Z-изображение (т.е. ряд прямого Z-преобразования при суммировании от минус бесконечности до плюс бесконечности сходится).
(физически реализуемые системы). Можно показать, что свойство справедливо, если обе последовательности отличны от нуля в области отрицательных времен и имеют Z-изображение (т.е. ряд прямого Z-преобразования при суммировании от минус бесконечности до плюс бесконечности сходится).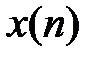 ,
, 







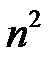













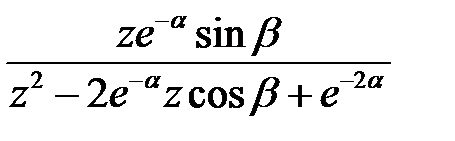





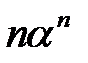









 и знаменателем прогрессии
и знаменателем прогрессии  . Ряд сходится тогда и только тогда, когда геометрическая прогрессия является бесконечно убывающей, т.е.
. Ряд сходится тогда и только тогда, когда геометрическая прогрессия является бесконечно убывающей, т.е.  или
или 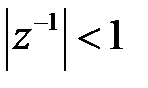 . Из последнего выражения следует область сходимости ряда в виде
. Из последнего выражения следует область сходимости ряда в виде



 . Ряд сходится тогда и только тогда, когда геометрическая прогрессия является бесконечно убывающей, т.е.
. Ряд сходится тогда и только тогда, когда геометрическая прогрессия является бесконечно убывающей, т.е.  . Из последнего выражения следует область сходимости ряда в виде
. Из последнего выражения следует область сходимости ряда в виде

 ,
, . Тогда, в соответствии с упомянутым свойством справедливо:
. Тогда, в соответствии с упомянутым свойством справедливо:
 , подставим в него
, подставим в него  вместо z и получим
вместо z и получим .
.



 , получим
, получим .
. (синус и косинус следует разложить по формуле Эйлера на комплексные экспоненты).
(синус и косинус следует разложить по формуле Эйлера на комплексные экспоненты).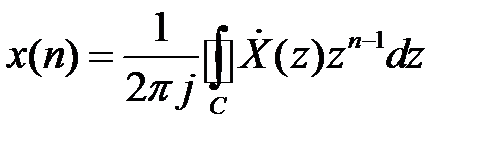
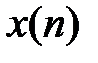 – искомая последовательность (дискретный сигнал),
– искомая последовательность (дискретный сигнал), 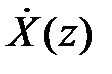 – z-изображение
– z-изображение 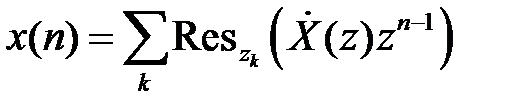 ,
, – вычет функции
– вычет функции  в полюсе
в полюсе  .
. для типовых дискретных сигналов являются дробно-рациональными функциями от z (т.е. функциями в форме отношения двух полиномов от z). Передаточные функции линейных дискретных систем (ЛДС) с постоянными параметрами
для типовых дискретных сигналов являются дробно-рациональными функциями от z (т.е. функциями в форме отношения двух полиномов от z). Передаточные функции линейных дискретных систем (ЛДС) с постоянными параметрами  также являются дробно-рациональными функциями. Тогда, z-изображение сигнала на выходе ЛДС
также являются дробно-рациональными функциями. Тогда, z-изображение сигнала на выходе ЛДС
 ,
, – i-й нуль, а
– i-й нуль, а  – k-й полюс подынтегрального выражения,
– k-й полюс подынтегрального выражения,  порядок i-го нуля, а
порядок i-го нуля, а  порядок k-го полюса. Очевидно, что нули являются корнями полинома числителя, а полюсы – корнями полинома знаменателя дробно-рациональной функции , а порядок нуля или полюса равен кратности соответствующего корня. В полиномы числителя и знаменателя разложены на множители с использованием их корней.
порядок k-го полюса. Очевидно, что нули являются корнями полинома числителя, а полюсы – корнями полинома знаменателя дробно-рациональной функции , а порядок нуля или полюса равен кратности соответствующего корня. В полиномы числителя и знаменателя разложены на множители с использованием их корней. ,
, справедливо
справедливо

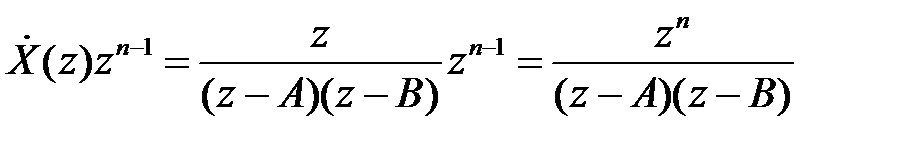
 и
и  , поэтому искомая последовательность определится суммой двух вычетов в указанных полюсах:
, поэтому искомая последовательность определится суммой двух вычетов в указанных полюсах: ,
,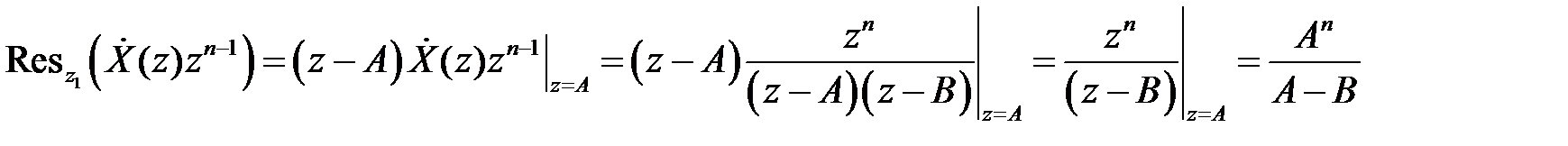

 ,
,

 . Тогда искомая последовательность полностью определится вычетом в этом полюсе:
. Тогда искомая последовательность полностью определится вычетом в этом полюсе:


 и
и  , поэтому искомая последовательность определится суммой двух вычетов в указанных полюсах:
, поэтому искомая последовательность определится суммой двух вычетов в указанных полюсах:

