 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Нормальное (гауссовское) распределение
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1 ОЗНАКОМЛЕНИЕ С СИСТЕМОЙ MATLAB. ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ТЕОРИИ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Преподаватель Павлов В.И. Подпись, дата Студент_________________________________ Прокудин И.А. Подпись, дата Группа СРБ-41 Тамбов 2012 Лабораторная работа 1 ОЗНАКОМЛЕНИЕ С СИСТЕМОЙ MATLAB. ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ ТЕОРИИ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
А)Ознакомление с системой программирования Matlab, приобретение навыков работы в ней. Б)Ознакомление с языком программирования системы Matlab. В)Исследование с помощью средств Matlab одномерных распределений теории вероятностей и математической статистики. Краткие теоретические сведения Сеанс работы с Matlab Сеанс работы с Matlab принято именовать сессией. Сессия, в сущности, является текущим документом, отражающим работу пользователя с системой Matlab. В ней имеются строки ввода, вывода и сообщений об ошибках. Строка ввода указывается с помощью приглашающего символа >>. В строке вывода символ >>отсутствует. Строка сообщений об ошибках начинается символами ???. Входящие в сессию определения переменных и функций располагаются в рабочей области памяти (workspace). Команды набираются на клавиатуре с помощью обычных операций строчного редактирования. Особое назначение имеют клавиши ↑ и ↓ . Они используются для подстановки после приглашения >>ранее введенных строк, например, для их дублирования, исправления или дополнения. Полезно сразу усвоить следующие команды: clc –очищает экран и размещает курсор в левом верхнем углу пустого экрана; clear– уничтожает в рабочем пространстве определения всех переменных; clear x– уничтожает в рабочем пространстве определение переменной x; clear a,b,c– уничтожает в рабочем пространстве определения переменных списка.
Построение графиков функций одной переменной Для построения графиков функций одной переменной y = f (x) в Matlab имеется функция plot.График строится в декартовой системе координат по заданным массивам значений аргумента и функции. Заданные этими массивами точки соединяются прямыми линиями. Имеется возможность изменять тип и цвет линии и тип узловых точек (маркер). Вызов этой функции осуществляется командой plot(x,y,s)где x, y– одномерные массивы одинаковой размерности; x –массив значений аргумента функции y = f (x); y– массив значений функции y = f (x); s –строковая константа, определяющая цвет u1083 линии, маркер узловых точек и тип линии. Эта константа может содержать от одного до трех символов. Цвет линии определяется символами y(желтый), m(фиолетовый), c(голубой), r(красный), g (зеленый), b(синий), w(белый), k(черный). Тип узловой точки определяется символами .(точка), o(окружность), x(крестик), +(плюс), * (звездочка), s(квадрат), d(ромб), < > ^(треугольники различной направленности), p(пятиугольник), h(шестиугольник). Тип линии определяется символами - (непрерывная), : (короткие штрихи), -. (штрихпунктир), -- (длинные штрихи). Символьную константу sможно опустить. В этом случае по умолчанию используется непрерывная линия желтого цвета.
Порядок выполнения работы
3.2.Для каждого распределения п. 1.2.8 вывести в отдельное графическое окно график функции распределения с использованием функций системы Matlab. Равномерное распределение
Текст программы: a=3; b=6; x=3.0001:0.0001:5.9999; y1=1; y2=(b-a); f=y1/y2; >> plot(x,f)
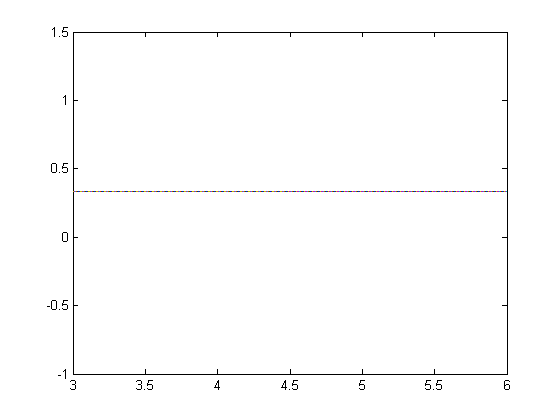 График 1 - Равномерное распределение
Нормальное (гауссовское) распределение
Текст программы:
>> a=25; >> sig=2; x=0:1:50; >> y1=1; y2=sqrt(2*pi*sig^2); y3=exp(-((x-a).^2/(2*sig.^2))); >> Fx=(y1/y2)*y3; plot(x,Fx)
 График 2- нормальное (гауссовское) распределение
|




