ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Условие неотрицательности переменных сохраняется в обеих задачах.
№ 24. Сформулируйте и докажите основное неравенство для взаимно двойственных задач линейного программирования. Сформулируйте достаточный признак оптимальности. Основное нер-во двойственности.Пусть Х – какое-нибудь допустимое решение задачи I, а У – какое-нибудь допустимое решение задачи II. Тогда справедливо неравенство f(x)<φ(Y) Доказательство:Имеем AX<B, откуда следует (АХ)T<BT или XTAT<BT. Умножим обе части этого неравенства справа на матрицу У>0=0, получим (XTAT)Y<BTY или, в ввиду ассоциативности умножения матриц, XT(ATY)<BTY=φ(Y) (I) Аналогично имеем ATY>С; умножив обе части слева на матрицу XT>0, будем иметь XT(ATY)>XTC=f(X) (II) Соединяя два полученных неравенства I и II, можем записать F(X)<XTATY< φ(Y), откуда и следует основное неравенство f(X)< φ(Y). Достаточный призрак опт-ти: Если для некоторых допустимых решений № 25. Сформулируйте первую и вторую теоремы двойственности. Докажите вторую теорему двойственности. Первая теорема двойственности. Если исходная задача имеет оптимальное решение, то и двойственная ей также имеет оптимальное решение. При этом оптимальные значения целевых функций обеих задач равны: fmax=gmin. Оптимальное решение исходной задачи можно найти по фор-ле: X=C*D-1 Вторая теорема двойственности. Если хотя бы одно оптимальное решение одной из двойственных задач обращает Если же i -я компонента хотя бы одного оптимального решения одной из двойственных задач положительна, то каждое оптимальное решение другой двойственной задачи обращает Доказательство:Пусть Они удовлетворяют следующим ограничениям:
Умножим (3), соответственно, на
Из основной теоремы двойственности следует
И с учетом (4) получаем:
Первое из этих выражений можем переписать в виде и так как все Аналогично получим: Вопрос №26. Приведите пример постановки транспортной задачи. Что такое оптимальный план перевозок? Что такое транспортная задача с правильным балансом? Сформулируйте критерий разрешимости транспортной задачи. 1) Классическая постановка транспортной задачи общего вида. Требуется найти план перевозок, при котором бы полностью удовлетворялся спрос всех потребителей, при этом хватало бы запасов поставщиков и суммарные транспортные расходы были бы минимальными. 2) Оптимальный план перевозок - такой план перевозок, который определяет минимальную суммарную стоимость транспортировки, не превышая объем производства каждого из поставщиков и полностью покрывая потребности каждого из потребителей. 3) Транспортная задача с правильным балансом. Теорема: если допустимое решение Х=(хij)*(i= Общее кол-во товара у поставщиков: Общая потребность в товаре в пунктах назначения: 4) Критерий разрешимости транспортной задачи: Транспортная задача разрешима только, если она имеет правильный баланс. №27. Опишите методы построения начального опорного плана транспортной задачи. 1) Метод северо-западного угла 2)Метод минимального тарифа Начальный опорный план находят, заполняя не более чем m+n-1 клеток (по числу базисных переменных). Любое допустимое решение транспортной задачи можно записать в транспортную таблицу. Клетки транспортной таблицы, в которых находятся отличные от нуля (или базисные нулевые) перевозки, называются занятыми, остальные свободными. Клетки таблицы нумеруются так, что клетка, содержащая перевозку xij, т.е. стоящая в i-строке и j- столбце, имеет номер (i,j). Каждой клетке с номером (i,j) соответствует переменная xij. Выбор заполняемых клеток производят, ориентируясь на тарифы перевозок, а именно: на каждом шаге выбирают какую-нибудь клетку (i,j), отвечающую минимальному тарифу и помещают в нее максимально возможную перевозку xij. После чего удаляют либо столбец, либо строку в зависимости от соотношения xij=bj или xij=ai. №28. Опишите метод потенциалов. Сформулируйте определения следующих понятий: свободная клетка, занятая клетка, оценка свободной клетки, цикл, перестановка по циклу. В чем состоит условие оптимальности опорного плана? 1) Метод потенциалов. Метод потенциалов основан на следующей теореме. Если допустимое решение Х=( xij) (i= ui+ vj<либо =сij, если xij=0. Равенства ui+ vj=сij при xij>0 используются для нахождения потенциалов. Данная система уравнений имеет m+n неизвестных ui,i= Неравенства ui+ vj<либо =сij при xij=0 используются для проверки оптимального опорного решения. Эти неравенства удобно записать в виде Числа 2) Клетки транспортной таблицы, в которых находятся отличные от нуля(или базисные нулевые) перевозки, называются занятыми, остальные – свободными. Оценка свободной клетки – (см. метод потенциалов) Цикл –такая последовательность клеток транспортной таблицы (i1,j1), (i1,j2), (i2,j2),…(ik,j1), в которой две и только две соседние клетки расположены в одной строке или столбце, причем первая и последняя клетки также находятся в одной строке или столбце. (?)Перестановка по циклу - (сдвиг по циклу на величину t)-увеличение объемов во всех нечетных клетках цикла, отмеченных знаком «+», на t и уменьшение объемов перевозок во всех четных клетках, отмеченных знаком «-», на t. 3) Условие оптимальности опорного плана. Оптимальный план должен определять минимальную суммарную стоимость транспортировки, не превышая объем производства каждого из поставщиков и полностью покрывая потребности каждого из потребителей. Оптимальный план перевозки соответствует минимуму линейной целевой функции f(X)=
|



 выполняется равенство значений целевых функций
выполняется равенство значений целевых функций  то х*, у* - оптимальные решения задачи I и II соответственно.
то х*, у* - оптимальные решения задачи I и II соответственно. и
и  – оптимальные решения пары двойственных задач. Тогда для
– оптимальные решения пары двойственных задач. Тогда для  ,
, 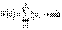
 . (3)
. (3) и
и 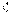 , и просуммируем полученные выражения:
, и просуммируем полученные выражения: . (4)
. (4) . (5)
. (5) ,
,  .
. ,
, и выражения в скобках неотрицательны, то опуская å, получим:
и выражения в скобках неотрицательны, то опуская å, получим:  .
. . Ч.Т.Д.
. Ч.Т.Д. , j=
, j=  ) транспортной задачи является оптимальным, то существует потенциалы поставщиков ui (i=
) транспортной задачи является оптимальным, то существует потенциалы поставщиков ui (i=  ) и потребителей vj(j=
) и потребителей vj(j=  ). Удовлетворяющее условиям: 1) ui+vj=cij, если xij>0; 2) ui+vj ≤cij, если xij=0.
). Удовлетворяющее условиям: 1) ui+vj=cij, если xij>0; 2) ui+vj ≤cij, если xij=0.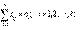
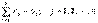

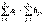
 , j=
, j=  ) транспортной задачи является оптимальным, то существуют потенциалы поставщиков ui(i=
) транспортной задачи является оптимальным, то существуют потенциалы поставщиков ui(i=  ij=ui+vj-cij при xij=0.
ij=ui+vj-cij при xij=0.
 min при ограничениях на потребление и поставку
min при ограничениях на потребление и поставку