 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ИССЛЕДОВАНИЕ ДИНАМИКИ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Минобрнауки РФ Санкт-Петербургский государственный электротехнический Университет имени В.И.Ульянова (Ленина) «ЛЭТИ» Факультет электроники Кафедра Физики
ОТЧЕТ По лабораторно-практической работе № 3 «ИССЛЕДОВАНИЕ ДИНАМИКИ ЗАТУХАЮЩИХ КОЛЕБАНИЙ» Выполнил: Варгин А.Э. гр. 3206 ФЭЛ Преподаватель: Белоногая Екатерина Сергеевна
“Выполнено” “____” ___________
Подпись преподавателя __________
ЛАБОРАТОРНАЯ РАБОТА 3 ИССЛЕДОВАНИЕ ДИНАМИКИ ЗАТУХАЮЩИХ КОЛЕБАНИЙ Цель работы: исследование динамики затухающего колебательного движения на примере крутильного маятника, определение основных характеристик диссипативной системы.
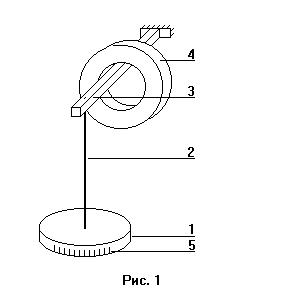
Приборы и принадлежности: крутильный маятник, секундомер. Применяемый в работе крутильный маятник (рис. 1) представляет собой диск 1, закрепленный на упругой стальной проволоке 2, свободный конец которой зажат в неподвижном кронштейне 3. На кронштейне расположено кольцо 4, масса которого известна. Кольцо 4 можно положить сверху на диск 1, изменив тем самым момент инерции маятника. На диске 1 установлен флажок, располагающийся под подставкой макета в ванночке с жидкостью. Поворачивая флажок, можно изменять момент сил сопротивления, действующих на маятник. Для отсчета значений угла поворота маятника служит градуированная шкала 5, помещенная на ободе диска 1.
Исследуемые закономерности Крутильный маятник. При повороте тела, закрепленного на упругом подвесе, в результате деформации сдвига при закручивании подвеса возникает возвращающий момент упругих сил M = -kj, где k - коэффициент кручения, зависящий от упругих свойств материала подвеса, его размеров и формы, j - угол поворота. При малых углах поворота, без учета сил трения в подвесе, крутильные колебания маятника являются гармоническими, а уравнение движения тела имеет вид
и является уравнением движения осциллятора с затуханием. Колебания такого осциллятора уже не будут гармоническими. Коэффициент b = R/2I называют коэффициентом затухания. Если
где
Крутильный маятник как диссипативная система Полная энергия колебаний маятника убывает со временем по закону
где Убывание энергии происходит за счет совершения работы против сил трения. Энергия при этом превращается в тепло, идет процесс диссипации энергии. Скорость диссипации энергии (мощность потерь)
Помимо коэффициента затухания b (или времени затухания t) и мощности потерь Pd колебательная диссипативная система характеризуется также добротностью Q , позволяющей судить о способности системы сохранять энергию. Добротность определяется отношением запасенной системой энергии к потерям энергии за время T/2p = 1/w. Легко видеть, что добротность
т.е. численно равна числу колебаний за время t = pt. За это время амплитуда колебаний уменьшается в ep @ 23 раза, а энергия колебаний в e2p @ 535 раз, иными словами, за это время колебания практически затухают. В технике для характеристики колебательных систем с затуханием вводят декремент затухания (D), или его логарифм – логарифмический декремент затухания (d = lnD), определяя эти параметры через отношение амплитуд колебаний, соответствующих соседним периодам
ЗАДАНИЕ ПО ОБРАБОТКЕ РЕЗУЛЬТАТОВ:
а1=6, а2=2
l=635 mm d=2.5 mm M=1821 г Dex=248 mm Din=58.4 mm D0=248 mm h0=38.1mm p=1.18*103 кг/м3
Расчетная формула: Тк= Tк1= Тк2= Тк3= Тк4= Тк5= Определяем погрешности ∆T с доверительной вероятностью p = 95%.
Упорядочим выборку объемом N=5: Tк min=1,674 RTк = Tк max – Tк min = 1,622-1,594=0,036 (сек) Проверка на промахи:
По результатам проведенных расчетов заключаем, что в нашей выборке промахи отсутствуют. Продолжаем далее статистическую обработку.
Рассчитываем среднее значение по формуле
Рассчитываем СКО среднего по формуле
Расчет случайной погрешности по формуле
Приборная погрешность секундомера, Вычислим полную погрешность
Запишем результат статистической обработки Tк=1,687
Расчетная формула: Тд= Tд1= Tд2= Tд3= Tд4= Tд5= Определяем погрешности ∆Tд с доверительной вероятностью p = 95%.
Упорядочим выборку объемом N=5: Tд min=1,144 Rд= Tд max – Tд min = 1,469-1,411=0,058(сек) Проверка на промахи:
По результатам проведенных расчетов заключаем, что в нашей выборке промахи отсутствуют. Продолжаем далее статистическую обработку.
Рассчитываем среднее значение по формуле
Рассчитываем СКО среднего по формуле
Расчет случайной погрешности по формуле
Приборная погрешность секундомера, Вычислим полную погрешность
Запишем результат статистической обработки Tд=1,168
Расчетная формула: С кольцом:
Определяем погрешности ∆
Упорядочим выборку объемом N=5:
Проверка на промахи:
По результатам проведенных расчетов заключаем, что в нашей выборке промахи отсутствуют. Продолжаем далее статистическую обработку.
Рассчитываем среднее по формуле
Рассчитываем СКО среднего по формуле
Расчет случайной погрешности по формуле
Приборная погрешность секундомера, Вычислим полную погрешность
Запишем результат статистической обработки
Без кольца:
Определяем погрешности ∆
Упорядочим выборку объемом N=5:
Проверка на промахи:
По результатам проведенных расчетов заключаем, что в нашей выборке промахи отсутствуют. Продолжаем далее статистическую обработку.
Рассчитываем среднее значение по формуле
Рассчитываем СКО среднего по формуле
Расчет случайной погрешности по формуле
Приборная погрешность секундомера, Вычислим полную погрешность
Запишем результат статистической обработки
Формула для расчета: С кольцом:
Определяем погрешности ∆τ с доверительной вероятностью p = 95%. Упорядочим выборку объемом N=5:
Проверка на промахи:
По результатам проведенных расчетов заключаем, что в нашей выборке промахи отсутствуют. Продолжаем далее статистическую обработку.
Учитывая приборную погрешность вычислим полную погрешность
Запишем результат статистической обработки
Без кольца:
Определяем погрешности ∆τ с доверительной вероятностью p = 95%. Упорядочим выборку объемом N=5:
Проверка на промахи:
По результатам проведенных расчетов заключаем, что в нашей выборке промахи отсутствуют. Продолжаем далее статистическую обработку.
Рассчитываем среднее по формуле при N=5, tp,N =2,8, p=95%.
Учитывая приборную погрешность, вычислим полную погрешность
Запишем результат статистической обработки
Расчетная формула: С кольцом:
Определяем погрешности ∆
Найдем среднее значение:
Определим полную погрешность где а
Запишем результат статистической обработки:
Без кольца:
Определяем погрешности ∆
Найдем среднее значение:
Определим полную погрешность где а
Запишем результат статистической обработки:
Iк=1/8*1.821*(0,2482 +0,05842) = 0.015(кг*м2)
Расчетная формула: Iд. Iд1= Iд1= Iд1= Iд1= Iд1= Определяем погрешности ∆Iд с доверительной вероятностью p = 95%. Найдем среднее значение :
Размах выборки составляет: Найдем СКО среднего по формуле
Расчет случайной погрешности по формуле С учетом приборной погрешности вычислим полную погрешность
Запишем результат статистической обработки:
Формула для расчета: Iд = Iд= 1. Определим коэффициент кручения материала подвеса.
2. Найдем среднее значение
3. Определим полную погрешность
Где
4. Запишем результат статистической обработки:k=
k=0.482 1. Определим модуль сдвига материала подвеса
2. Найдем среднее значение
3. Определим полную погрешность
4. Запишем результат статистической обработки:
G=204.496 1.Определим полную энергию маятника
1. Определим мощность потерь маятника
1. Определим добротность маятника
Сведем все промежуточные вычисления и полученные результаты в таблицу.
ВЫВОД: Выполнив данную лабораторную работу, мы провели исследование динамики колебательного движения крутильного маятника. Во время этого исследования экспериментальным путем был получен ряд данных, на основании которых мы рассчитали период колебаний маятника без кольца и с кольцом, время затухания маятника, собственную частоту его колебаний, а также экспериментальный момент инерции диска маятника.
|



 , где частота собственных колебаний гармонического осциллятора
, где частота собственных колебаний гармонического осциллятора 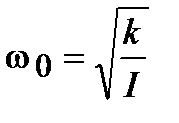 , I – момент инерции диска крутильного маятника. Сопротивление движению маятника (трение) создает тормозящий момент, пропорциональный скорости движения маятника,
, I – момент инерции диска крутильного маятника. Сопротивление движению маятника (трение) создает тормозящий момент, пропорциональный скорости движения маятника,  , где R - коэффициент сопротивления. С учетом сил сопротивления уравнение движения маятника принимает вид
, где R - коэффициент сопротивления. С учетом сил сопротивления уравнение движения маятника принимает вид 
 , движение крутильного маятника описывается уравнением затухающих колебаний
, движение крутильного маятника описывается уравнением затухающих колебаний ,
, - начальная амплитуда колебаний маятника, t = 1/b - время затухания, определяющее скорость убывания амплитуды A(t) маятника, численно равное времени, за которое амплитуда убывает в e раз (рис. 2), т.е.
- начальная амплитуда колебаний маятника, t = 1/b - время затухания, определяющее скорость убывания амплитуды A(t) маятника, численно равное времени, за которое амплитуда убывает в e раз (рис. 2), т.е.
 при t = t
при t = t  , w - частота колебаний осциллятора с затуханием, связанная с собственной частотой соотношением
, w - частота колебаний осциллятора с затуханием, связанная с собственной частотой соотношением  . Время затухания t также выражается через момент инерции I и коэффициент сопротивления R выражением
. Время затухания t также выражается через момент инерции I и коэффициент сопротивления R выражением 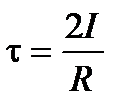 .
. 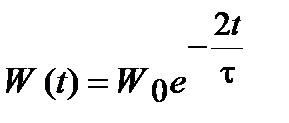 ,
, - начальная энергия колебаний.
- начальная энергия колебаний. .
.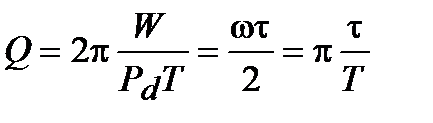 ,
, или d = bT.
или d = bT. , где tк – время, за которое совершались колебания, n=10 – количество колебаний, совершенных маятником.
, где tк – время, за которое совершались колебания, n=10 – количество колебаний, совершенных маятником. =1,691 (сек)
=1,691 (сек)
 =1,71 (сек)
=1,71 (сек) =1,674 (сек)
=1,674 (сек) =1,675 (сек)
=1,675 (сек) =1,688(сек)
=1,688(сек) 1,675
1,675  1,688
1,688  не промах
не промах не промах
не промах не промах
не промах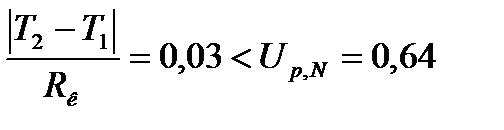 не промах
не промах
 к= 1,687(сек)
к= 1,687(сек)
 = 0,006 (сек)
= 0,006 (сек)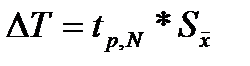
 (сек)
(сек) =0,01(сек)
=0,01(сек)
 = 0,019 (сек)
= 0,019 (сек) с p=95%:
с p=95%: 0,019(сек)
0,019(сек) , где tд – время, за которое совершались колебания, n=10 – количество колебаний, совершенных маятником.
, где tд – время, за которое совершались колебания, n=10 – количество колебаний, совершенных маятником. =1,197 (сек)
=1,197 (сек) =1,153 (сек)
=1,153 (сек) =1,144(сек)
=1,144(сек) =1,187(сек)
=1,187(сек)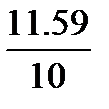 =1,159(сек)
=1,159(сек) не промах
не промах не промах
не промах не промах
не промах не промах
не промах = 1,168 (сек)
= 1,168 (сек) = 0,010 (сек)
= 0,010 (сек)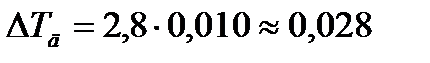 (сек)
(сек) = 0,03(сек)
= 0,03(сек) к и
к и  д для маятника с кольцом и без кольца:
д для маятника с кольцом и без кольца: =
=  , где Т – период колебаний.
, где Т – период колебаний. =3,753 (сек-1)
=3,753 (сек-1) =3,751 (сек-1)
=3,751 (сек-1) =3,722 (сек-1)
=3,722 (сек-1) =3,715 (сек-1)
=3,715 (сек-1) =3,674(сек-1)
=3,674(сек-1) с доверительной вероятностью p = 95%.
с доверительной вероятностью p = 95%. =
=  не промах
не промах не промах
не промах не промах
не промах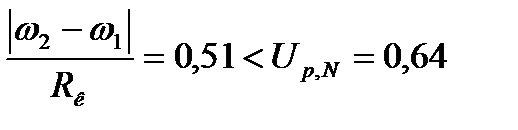 не промах
не промах
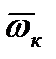 = 3,723 (сек-1)
= 3,723 (сек-1)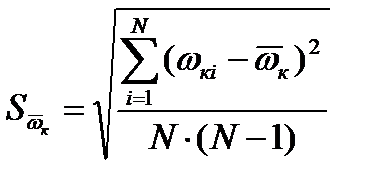
 = 0,014 (сек-1)
= 0,014 (сек-1)
 (сек-1)
(сек-1)
 = 0,04(сек-1)
= 0,04(сек-1) с p=95%
с p=95% =3,72
=3,72  =5,492 (сек-1)
=5,492 (сек-1) =5,449 (сек-1)
=5,449 (сек-1) =5,421 (сек-1)
=5,421 (сек-1) =5,293 (сек-1)
=5,293 (сек-1)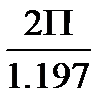 =5,249 (сек-1)
=5,249 (сек-1) с доверительной вероятностью p = 95%.
с доверительной вероятностью p = 95%. min=5,249
min=5,249  max
max =
=  max –
max –  min = 5,492-4.5,249=0,243 (сек-1)
min = 5,492-4.5,249=0,243 (сек-1) не промах
не промах не промах
не промах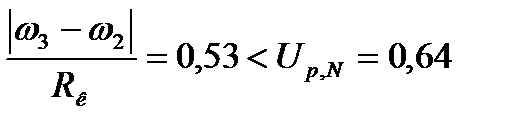 не промах
не промах не промах
не промах = 5,3808 (сек-1)
= 5,3808 (сек-1) (сек-1)
(сек-1)
 = 0,131 (сек-1)
= 0,131 (сек-1) с p=95%
с p=95% =5,38
=5,38  к и
к и  д для маятника с кольцом и без кольца:
д для маятника с кольцом и без кольца: , где tз – время затухания, за которое амплитуда колебания уменьшается примерно в два раза.
, где tз – время затухания, за которое амплитуда колебания уменьшается примерно в два раза.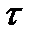 з.к.1=
з.к.1=  =19,7(сек)
=19,7(сек) =16,52(сек)
=16,52(сек) =16,87(сек)
=16,87(сек) =17,10(сек)
=17,10(сек) =17,48(сек)
=17,48(сек) min=16,52
min=16,52  16,87
16,87 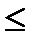 17,10
17,10  =
=  не промах
не промах не промах
не промах не промах
не промах не промах
не промах


 = 0,56(сек)
= 0,56(сек)


 = 1,59 (сек)
= 1,59 (сек) с p=95%
с p=95% =17,53
=17,53  =16(сек)
=16(сек) =15,3(сек)
=15,3(сек) =16,5(сек)
=16,5(сек) =16,32(сек)
=16,32(сек) =16,73(сек)
=16,73(сек) min=15,3
min=15,3  max
max max -
max -  min= 1,43(сек)
min= 1,43(сек) не промах
не промах не промах
не промах не промах
не промах не промах
не промах
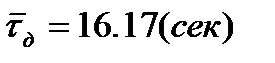



 = 0,74 (сек)
= 0,74 (сек) с p=95%
с p=95% =16,17
=16,17  к0 и
к0 и 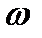 д0 для маятника с кольцом и без кольца.
д0 для маятника с кольцом и без кольца. , где
, где  - коэффициент затухания колебаний маятника.
- коэффициент затухания колебаний маятника. =3.674(сек-1)
=3.674(сек-1) =3.715(сек-1)
=3.715(сек-1) =3.722(сек-1)
=3.722(сек-1) =3.751(сек-1)
=3.751(сек-1) =3.753(сек-1)
=3.753(сек-1)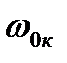 как косвенные измерения методом полного дифференцирования с доверительной вероятностью p = 95%.
как косвенные измерения методом полного дифференцирования с доверительной вероятностью p = 95%. =3.723(сек-1)
=3.723(сек-1) ,
, 0,99988,
0,99988, =-0.0000498
=-0.0000498 =0,04 (сек-1)
=0,04 (сек-1) =3.72
=3.72  0,04 (сек-1)
0,04 (сек-1)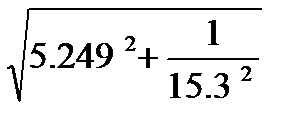 =5.249(сек-1)
=5.249(сек-1) =5.293(сек-1)
=5.293(сек-1) =5.421(сек-1)
=5.421(сек-1) =5.449(сек-1)
=5.449(сек-1) =5.492(сек-1)
=5.492(сек-1) как косвенные измерения методом переноса полного дифференцирования с доверительной вероятностью p = 95%.
как косвенные измерения методом переноса полного дифференцирования с доверительной вероятностью p = 95%. = 5.39(сек-1)
= 5.39(сек-1) ,
, 0,99993,
0,99993, =-0.0000438
=-0.0000438 =0,13(сек-1)
=0,13(сек-1) =5.39
=5.39  ), где
), где  - внешний диаметр кольца, M- масса кольца,
- внешний диаметр кольца, M- масса кольца,  - внутренний диаметр кольца.
- внутренний диаметр кольца.
 =0.01441(кг*м2)
=0.01441(кг*м2) =0.01456(кг*м2)
=0.01456(кг*м2) =0.01338(кг*м2)
=0.01338(кг*м2) =0.01351(кг*м2)
=0.01351(кг*м2) =0.01314(кг*м2)
=0.01314(кг*м2)
 = 0.0138(кг*м2)
= 0.0138(кг*м2) 0,00142 (кг*м2)
0,00142 (кг*м2)
 0.0003 (кг*м2)
0.0003 (кг*м2)
 0,0003*2.8=0,00084(кг*м2)
0,0003*2.8=0,00084(кг*м2)
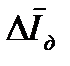 =0,0026(кг*м2)
=0,0026(кг*м2) =(0.01472±0.0026) (кг*м2)
=(0.01472±0.0026) (кг*м2) , где
, где  - плотность материала, из которого изготовлен диск; h0 – толщина диска маятника; D0 – диаметр диска маятника.
- плотность материала, из которого изготовлен диск; h0 – толщина диска маятника; D0 – диаметр диска маятника. = 0,27 (кг*м2).
= 0,27 (кг*м2).

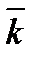 =0.428(H*м)
=0.428(H*м)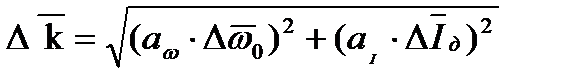
 =
= 
 =
= 
 =0.035(Н*м)
=0.035(Н*м)



 =204.496(Па).
=204.496(Па).
 =
= 
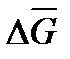
 ,
,  следовательно
следовательно 



 , сек-1
, сек-1 , сек-1
, сек-1 , сек
, сек