 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Максимально возможная ошибка одного измерения 12
Необходимо выяснить, как будут влиять ошибки измерения отдельных величин на искомую величину определяемую при помощи формулы. Разберем этот вопрос в общем виде. Пусть искомая величина W является функцией нескольких (допустим, трех) величин, измеряемых непосредственно в опыте:
Если бы ошибки в измерении величин x,y и zбыли бесконечно малыми, то ошибка в величине w, определялась бы ее полным дифференциалом:
В действительности, ошибки в измерения величин x, yи zне будут бесконечно малыми, однако для расчета величины ошибки можно воспользоваться аналогичной формулой, подставляя вместо dx, dyи dzдействительно конечные величины ошибок Δx, Δyи Δz. Итак, получаем:
где Δw - максимально возможная абсолютная ошибка искомой величины w; Δx, Δyи Δz - абсолютные ошибки в измерении величины x, yиz По формуле (69) вычисляется максимально возможная ошибка, поэтому все ее члены берутся по абсолютному значению и суммируются. В действительности, при проведении измерений ошибка может быть значительно меньше, так как входящие в (69) слагаемые могут иметь разные знаки, однако в наихудшем варианте все три слагаемые будут иметь один и тот же знак, что даст максимально возможную ошибку. Часто требуется найти максимально возможную относительную ошибку δw=Δw/w . Её можно получить, разделив (69) на W, т.е.:
Формула (70) является общей, по ней можно вычислить максимально возможную ошибку искомой величины w при любой функциональной зависимости w=f(x,y,z). Для выражения δw в процентах формулу (70) следует умножить на 100. В дополнение к общей формуле рассмотрим несколько частных случаев. Очень часто встречается случай, когда искомая величина w определяется как произведение измеряемых величин x, yиz в различных степенях и постоянной А, т.е.:
Причем α, βи γмогут быть любыми положительными или отрицательными числами. Заметим, что формула (72) охватывает случаи, описанные формулами (67) и (68). Для функциональной зависимости (71) можно получить более конкретное выражение для подсчета максимально возможной относительной ошибки величины. Возьмем производные, входящие в (70):
Подставив в (70) эти значения и значение w по (71), получим:
Откуда:
Обозначая относительные ошибки величин, непосредственно измеряемых в опыте:
Окончательно получаем:
Эта формула еще больше упрощается, если α, βиγ равны единице или единице с минусом. Тогда получим:
Последнее можно сформулировать следующим образом: если искомая Разберем другой случай. Пусть:
Определим величину максимально возможной относительной ошибки. Согласно (70) получим:
Однако чаще всего бывает желательно выразить относительную ошибку искомой величины через относительные ошибки величин, измеряемых в опыте, а не через абсолютные, как это сделано в формуле (79). Для этого преобразуем каждое слагаемое в (79):
Тогда для функциональной зависимости (78) получим формулу для расчета ошибки:
Вполне естественно, что формулы (70) - (81) могут быть распространены на любое число переменных. Величина относительной ошибки искомой величины в (76), (77) и (81) будет выражена в процентах, если δx, δyиδz подставляются также в процентах. Особо следует остановиться на случае, когда искомая величина w определяется как разность двух измеряемых в опыте величин, т.е.:
Если величины x и у близки друг другу по величине, то вследствие погрешностей этих величин искомое значение w может получиться с очень большой ошибкой, что совершенно неприемлемо. Разберем следующий пример. Пусть величина x = 50 и измерена с точностью ± 1, т.е. с ошибкой ± 2 %. Пусть величина y = 45 и измерена с точностью также ± 1, т.е. ошибка составляет ± 2,22 %, Вычислим величину w совместно с максимальной абсолютной погрешностью:
Таким образом, несмотря на то, что погрешность в измерениях xиy так уж велика (2 и 2,22 %), погрешность в искомой величине получается очень большая, т.е.:
Применяя к этому случаю формулу (81), получаем тот же результат:
В таблице. 1 приведены формулы для расчета максимально возможной относительной ошибки для некоторых функциональных зависимостей. В этой таблице через А, В, С, Д; α, β, γ и l обозначены численные коэффициенты, а через x, y, zи υ - величины, непосредственно измеряемые в эксперименте; δx, δy, δzи δυ - относительные ошибки измеряемых величин, а δw - максимально возможная относительная ошибка искомой величины.
3. Повышение точности и вычисление вероятной ошибки при многократных измерениях.
Выше уже говорилось о том, что при проведении многократных измерений заданной величины при одних и тех же параметрах случайные ошибки проявляются в разбросе получаемых данных. Если проведено несколько измерений искомой величины, то вполне Абсолютная случайная ошибка при нескольких измерениях величины
В этой формуле n - число измерений, wcp - среднеарифметическое значение из всех полученных величин w т.е.:
Ошибка, вычисляемая по (83), называется квадратичной. Из самого вида (83) ясно, что при n → ∞ ошибка Δwкв → 0. Однако функция (83) такова, что увеличение количества измерений с 2 до 5 сильно снижает эту ошибку; с 5 до 10 - несколько меньше, а увеличение количества измерений, например с 20 до 30, уже очень мало меняет величину этой ошибки. Заметим, что для вычисления рассматриваемой ошибки необходимо иметь полученные в результате эксперимента величины w, что не всегда требовалось для оценки ошибки отдельного измерения.
12 |








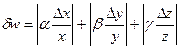






 Приведенный пример показывает, что надо крайне осторожно идти на такие измерения, при которых приходится вычитать близкие друг к другу по величине числа.
Приведенный пример показывает, что надо крайне осторожно идти на такие измерения, при которых приходится вычитать близкие друг к другу по величине числа.