 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задания на контрольную работу
Схема 2 Схема 3 Редуктор со сдвоенными сателлитами. Передаточное отношение определяется формулой: Редуктор используется в диапазоне «,„=7*25. Знак передаточного отношения всегда положителен. Редуктор Давида. Передаточное отношение определяется формулой: 2,2, Знак и$ может быть «+» и «-» в зависимости от отношения величин зуЗбеа колес. Вели число зыВыВ колес тако&о, гто 2, 2г' то Ичн-+0, Л иН1-+со-
Редуктор используетс передачах, так как КПД эти
К сложным планетарным механизмам относятся механизмы, состоящие из простого планетарного механизма и последовательно соединенной с ним зубчатой передачи или передачи другого типа (рис. 26), а также из двух или нескольких последовательно соединенных простых планетарных механизмов (рис. 25). Передаточное отношение таких механизмов аналитически определяется как произведение передаточных отношений отдельных ступеней, графически - строится план скоростей для всего механизма. Если оси валов (входного и выходного) не находятся на одной прямой (зубчатый механизм несоосный). то для определения передаточного отношения графически, линию скоростей несоосного колеса переносят (параллельно самой себе) в центр выбранной системы координат окружных скоростей. Обычно это ось центральных колес планетарного механизма (рис.2б)- Пример 1. Определить передаточное отношение ишг сложного планетарного редуктора, представленного на рис. 25 ■ Аналитический метод: Графический метод. Чертится план механизма в выбранном масштабе, /л1У см. рис. 25. Строится общий план скоростей для обеих ступеней сложного планетарного механизма. Для чего выбирается система координат уох, в которой откладывается произвольный вектор скорости (•) А звена 1, уА. Линия скоростей 1 колеса проводится через (•) О (м.ц.с. солнечного колеса 1) и вершину вектора Ул. Мгновенный центр скоростей сателлита 2 находится в (•) В. Проводим линию скоростей сателлита 2. В (•) С скорость сателлита 2 и водила Н1 совпадают. Проводим линию скоростей водила /-/,, которая является одновременно и линией скоростей колеса 4 (водило Н1 и колесо 4 жестко связаны). В (•) Д скорости звена 4 и звена 5 совпадают уд<=У/ц. Мгновенный центр скорости блока сателлитов 5-5' находится в (•) Е (центральное колесо 6 неподвижно). Проводим линию скоростей блока сателлитов 5-5'. В (•) Р скорость Уеъ = Уг„г. Проводим линию скоростей водила Н2. План скоростей построен. На произвольном расстоянии ОР проводим линию МК // х-х на которой образовались отрезки 1.Р и МР. Передаточное отношение Знак передаточного отношения положительный (отрезки МР и 1Р лежат в одной четверти). *
я р> I (О X (О О 1- о X о. ф Ж го С; с о I О е о о. о I ГО с: М-) сч О.
Пример 2. Определить передаточное отношение сложного планетарного редуктора, представленного на рис. 26. Аналитический метод. Графический метод. Чертится план механизма в выбранном масштабе, //Л, см. рис. 26. Строим план скоростей. Выбираем систему координат, в которой задаем произвольно вектор V л окружной скорости солнечного колеса 1 в (•) А, Ул, = Ул2. В (•) В м.ц.с. сателлита, к,. =о. Проводим линию скоростей сателлита.
Рис. 26. В (•) С, Ус2=Усн. Про-водим линию скоростей водила, она же -линия скоростей колеса 4 (водило и колесо 4 жестко связаны). В (•) Д, Уд4 = уД5. Проводим линию скоростей колеса 5. Для определения передаточного отношения и15 линию скоростей колеса 5 параллельно самой себе переносим в (•) О, тогда: и15=-ю>/рм. Знак передаточного отношения отрицательный (отрезки КР и РМ лежат в разных четвертях). 2.4.4. Условия сборки, соседства, соосности планетарных механизмов При проектировании планетарного редуктора с заданным передаточным отношением необходимо выполнение условий: соосности, соседства, сборки. Условие соосности.Это условие, при котором оба центральных зубчатых колеса и водило должны иметь общую геометрическую ось вращения. Это условие может быть записано: 2, +г2=23-22 для схемы 1 - редуктор Джемса; 2, +22 = 23 -г, для схемы 2 - редуктор со сдвоенными сателлитами; 2, +22 = 2,+22, для схемы 3 - редуктор Давида; 2, - г2 = 2, - 2, для схемы 3 - редуктор Давида. Условие соседства.Это условие, при котором все сателлиты, размещенные в одной плоскости, равноудалены и не задевают друг друга. Условие записывается в виде неравенства: (г, +22)иттг/р > 22 +2 - для внешнего зацепления (тг= 180°); р - число сателлитов. [2,-2 ,}зшЯ7/?>2 ,+2 - для внутреннего зацепления. Условие сборки.Это условие, при котором зубья всех промежуточных колес (сателлитов) могут войти в правильное зацепление с зубьями центральных колес 1 и 3 . Условие выражается: 1. Для редуктора Джемса (схема 1): 2,+23=кр, где Р - число сателлитов; К - любое целое число. 2. Для остальных редукторов (схема 2, 3): 2 2 ц„ --^- = к-р', где: р' - число блоков сателлитов; Э - наибольший общий делитель чисел 2, и 2,; К-любое целое число. В силовых планетарных редукторах применяют, возможно, большее И,„=7 Япю=4 И,я=4 С =6-7 Пример 1. Проверить условия соосности, соседства, сборки для редуктора Джемса (рис. 26), число зубьев 2, = 20 и 22= 36. Определяем число зубьев опорного колеса по условию соосности:
Определяем передаточное отношение редуктора Джемса: 7 47 иш=\ + =± = 1 + — = 5,6. В зависимости от, передаточного отношения выбираем число сателлитов: р=4. Проверяем условие соседства: а) (г, +22)зтШ°//> > 1г +2 - для внешнего зацепления, (20 + Зб)зт180°/4 > 36 + 2, 39,59 > 38 - условие соблюдается; б) (гг-22)этт°/р>2 +2 -для внутреннего зацепления, (92-Зб)8ш180°/4 > 36 + 2, 39,59 > 38 - условие соблюдается. Проверяем условие сборки: 2,+23=к-р, 20+92 = к-4, 112 = 28-4 - условие соблюдается. Пример 2. Проверить условия соосности, соседства, сборки редуктора со сдвоенными сателлитами (рис. 25), числом зубьев 24=20, 25 =40, 26 =80. Определяем число зубьев колеса 5' по условию соосности: 2< + 25=26-2$,, 20 + 40 = 80-25,, 25,=20. Определяем передаточное отношение редуктора со сдвоенными сателлитами: и4н =13^=1+^°=9. 4Н' 2,25. 20-20 В зависимости от передаточного отношения выбираем число блоков сателлитов р' = 3. Проверяем условие соседства; а) (24 +25)8т180°/з > 25 + 2 - для внешнего зацепления, (20 + Зб)8ю60° >40 + 2, 51,9 > 42 - условие соседства выполняется; б) (26-2,)зт180о/з>2, + 2 -для внутреннего зацепления, (80-20)8Н1бО° > 20 + 2, 51,9 > 22 - условие соседства выполняется. Проверяем условие сборки: 9-20-20/п = к-з, 9-400/200=6-3 - условие сборки выполняется. Пример 3. Проверить условия соосности, соседства, сборки редуктора Давида (рис.24), с числами зубьев г, =30, г2=18, 22,=20, 23 =28. Проверяем условие соосности: 30 + 18 = 20 + 28, 48 = 48 - уСЛОВИв СООСНОСТИ ВЫПОЛНЯвТСЯ. Определяем передаточное отношение редуктора Давида: Мш=1_ад=1_1^=о;84. 2,22. 30-20 Редуктор Давида - это не силовой редуктор, т.е. большую мощность через редуктор передать нельзя, поэтому число блоков сателлитов равно р' = 3. Проверяем условие соседства: а) (2, +г2)81п180°/з > 22+2 - для внешнего зацепления, (30+18)зшб0° > 18 + 2, 41,76 > 20 - условие соблюдается. б) (г3+2:2,)5т180о/з>22, + 2 -для внешнего зацепления, (28 + 20)зт60° > 20 + 2, 41,76 > 22 - условие соблюдается. Проверяем условие сборки: 2,2, 0,84.30-20/Х) = >(:-3, 0,84-600/6 = 28-3, 84 = 84 - условие сборки соблюдаются. 2.4.5. Коэффициент полезного действия зубчатых передач Потери мощности в зубчатых передачах складываются из потерь: на трение в зацеплении, на трение в подшипниках, из гидравлических потерь на размешивание и разбрызгивание масла. КПД простой передачи вычисляется: где: Т]г - КПД зубчатой передачи: 7з = 0,95+0,98 -для цилиндрической ступени; 7з = 0,96+0,97 - для конической ступени; Т]ъ = 0,7+0,9 - для червячной ступени. Г\п- КПД, учитывающий потери в одной паре подшипников: 77„= 0,99+0,995 - для подшипников качения;
7]„ = 0,97-0,99 - для подшипников скольжения; т - число пар подшипников в передаче; г/г- КПД, учитывающий гидравлические потери, связанные с перемешиванием и разбрызгиванием масла в корпусе передачи (Т]г = 0,97-0,98). В многоступенчатом зубчатом ряде передача мощности от ведущего колеса к ведомому осуществляется последовательно, цепочкой (рис. 27>
В планетарной передаче поток мощности на солнечном колесе 1 разветвляется и идет на сателлиты (рис. 28')- С каждого сателлита часть мощности идет к опорному колесу, часть - на водило. На валу водила мощность с потерями собирается от всех сателлитов. У опорного колеса [(•)к] часть мощности теряется. Поэтому КПД планетарного механизма можно вычислить по формулам табл. 1.
В таблице 1. ц' - КПД обращенного планетарного механизма, полученного путем остановки водила. Если при передаче движения от колеса к водилу значения передаточного отношения и^ лежат в пределах 0 < и1н<1-т|' или 0 > и1н>1-1/ ц', то КПД планетарного редуктора будет отрицательным. Это означает самоторможение, т.е. передача движения от колеса к водилу невозможна. При передаче движения от водила к колесу КПД планетарного механизма всегда больше нуля и самоторможение в этом случае не может иметь места, но при и1н-> 0, ц -> 0. Пример. Определить КПД сложного планетарного механизма, 24 = 20, 25 = 40, 26 = 80, 25'=20. а) Нт. = 5,6 (определено ранее). При передаче мощности от колеса 1 к водилу Н1 и условии ищ >1 выбираем формулу для определения г|1н1 (см. табл. 1). Пая =------ Л--П'-П-"!„,,>/. "|я, тГ = Ли-Лаз = 0,95- 0,95 = 0,9. ^л=77[1-0,9(1-5,6)] = 0,92 5,0 б) иЛНг = 9(определено ранее). При передаче мощности от колеса 4 к водилу Н2 и при и^г >1 ^=^[1-0,9(1-9)] = 0,91 I П' = -П.45 "Ли = 0.95 • 0,95 = 0,90, г,1Н2 = 0,92 -0,91= 0,84.
Простая зубчатая передача При проведении силового расчета будем предполагать: колеса вращаются равномерно^- СО, =сот(, центры масс колес лежат на осях, таким образом колеса уравновешены и центробежные силы инерции равны нулю. При передаче вращающего момента в точке контакта зубьев возникает сила нормального давления Рп и сила трения Ртр. Сила Рп направлена по нормали к поверхности профиля зуба, т.е. по линии зацепления NN. Сила трения Р^ = Рпт вызывает скольжение профилей зубьев. Сила Ртр « Р„, поэтому силой трения пренебрегают. Для удобства расчетов силу взаимодействия между зубьями Рп принято прикладывать и определять в полюсе зацепления. Ведомое колесо - колесо 2, к нему приложен момент М2 (или момент сопротивления), направленный противоположно направлению угловой скорости ©,. Силы взаимодействия колес Р12 и Р21 приложены в т. Р (полюс зацепления) и направлены по нормали к профилям зубьев или по линии зацепления N - N. Сила Р21 - сила реакции со стороны ведомого колеса 2 на ведущее колесо 1. Сила Р12 - сила реакции со стороны ведущего колеса 1 на ведомое колесо 2. Ориентация сил реакции в зацеплении определяется углом зацепления СЛ„, (углом между нормалью N - N и касательной I -1).
Рис. 29. Силы, которые действуют в зацеплении На рис. 29 показаны силы, которые действуют в зацеплении, при работе передачи (редуктора). Т - радикальное усилие, Р - окружное усилие. Окружное усилие передает крутящий момент, радикальное усилие, в конечном итоге, воспринимает подшипник и корпус. Силовой расчет зубчатых механизмов сводится к определению усилия в зацеплении (в полюсе зацепления Р) и на опорах валов. Пример. Рассмотрим силовой расчет зубчатого механизма с внешним и внутренним зацеплением (рис. 30,31). Ведущим колесом является колесо 1, к нему приложен уравновешивающий момент М^ (или движущий момент). Направление М-| совпадает с направление/4 Сд±.
Рис. 30. Зубчатый механизм с внешним зацеплением Для определения того, в какую сторону надо откладывать угол а" между нормалью N - N и клсдтвльнои Ь -Ъ , есть правило: 1. Если ведущим колесом является колесо с внешним зацеплением (рис. 30), то поворачивая вектор скорости V* точки касания Р на угол а„, в сторону, противоположную направлению угловой скорости со, ведущего колеса, найдем положение нормали N - N (примем ос»'=200).
При силовом расчете рассматривают равновесие колес, образующих статически определимые системы. Расчет обычно начинают с ведомого колеса, к которому приложен момент сопротивления М2. Колесо 2 является статически определимой системой, на него действует момент М2, реакция Р12 ведущего колеса 1 на ведомое колесо 2 и реакция стойки на колесо.
Рис. 31. Зубчатый механизм с внутренним зацеплением Рассматриваем равновесие колеса 2: 1. Ем«! =0; М2 ~Р,г •а = о (внутреннее зацепление) Р = М> ■ Ъ = г г2со%(Х„ Ри = ~4 \г. = гг с<ясс„; аа = 20°. 2. Х!^ = 0 (Для колеса 2) Рассматриваем равновесие ведущего звена 1: М, = Му = Рг1 ■ г, со%СС№ . , 2. 2? = о (Для колеса 1) ?21+?о, =о; Рп=-Рг1. В конце расчета проверяем равенство м,сох =м2со2 (в предположении, что потерь мощности в механизме нет, КПД равен единице), или м,^-=л/2; мхиа =мг. 2.4.6.2. Планетарный редуктор Силовой расчет планетарного редуктора сводится к определению усилий в зацеплении зубчатых колес, в подшипниках водила и опорах налов. Силовой расчет планетарного редуктора начинают с солнечного колеса, а не с водила. Пример 1. Провести силовой расчет планетарного редуктора, у которого иедущим является водило Н, а ведомое - солнечное колесо 3. Солнечное колесо нагружено внешним моментом сопротивления Мс = М3, рис. 32.
Рис. 32. Планетарный редуктор Решение. 1. Схема механизма строится с учетом выбранного масштабного 2. По формуле Виллиса определяем величину и знак знак - положительный, значит направление а)н (ведущее звено) совпадает с направлением (оъ (ведомое колесо). На схеме механизма указываем направления моментов: Мд = Мн (движущий момент), Мс = М3 (момент сопротивления). 3. Рассмотрим колесо 3. Колесо 3 - ведомое, колесо 2' - ведущее
действием момента М3 и сил реакции Рг-з и Роз-
Рис. 33. Равновесие колеса 3 Отметим, что в редукторе имеется р сателлитов (р = 3). Силовой расчет проводится по одному сателлиту, исходя из этого, вычислим новое значение момента на колесе 3: М3' = М3 / р. I 4. Рассмотрим блок сателлитов 2-2' (колеса 2 и 2' жестко связаны между собой). Сателлиты находятся в равновесии под действием сил Рзу, Р12иРНо(рис. 34). Считаем: колесо 2' - ведущее; колесо 2 - ведомое; колесо 1 -условно ведущее. Наносим направления угловых скоростей сателлитов. Определим положение линии действия силы Р12, для этого поворачиваем вектор окружной скорости р^, по направлению вращения Щ, Равновесие блока сателлитов 2 - 2': ^М0(р) = 0; Рп-г2 созО^ -/»ц,,г, соза№ =0 Г2'СО$С1 Г2 Векторное уравнение решаем графически. В масштабе (ЛР строим план сил. Из плана сил определяем рио =~ас/лр.
5. Рассматриваем ведущее звено - водило Н (рис. 35)-
Каждая ветвь водила действием силовых факторо стороны сателлита. Из условия равновесия во 2ХИ-°, Р2Нь-м[=о, м ме=м'ер, где р - число с Сателлиты при р > 1 уравновешивают водило. %Р = 0, Р2н+Рон=0, Р1н=-Р0Н. 6. Проверка точности уравнение мощности на входе мп(Ои =мса>3, при услов Рис. 34, Равновесие сателлитов 2-2'
Пример 2. Провести силовой расчет сложного планетарного редуктора, представленного на рис. 36. Алгоритм расчета: 1. Вычерчиваем механизм и его ступени с учетом выбранного масштабного коэффициента /л^м/мм]. 2. Вычисляем передаточное отношение механизма щ. По знаку передаточного отношения определяется направление вращения ведущего (1) или ведомого (5) колес. Направление вращения одного из колес задано. 3. Исходя из энергетического равенства редуктора (при 77^=1) определяем момент движущих сил Мд (Мс дано). 4. Из равновесия колес 4-5 (цилиндрическая зубчатая передача) определяем М4 = Мн, момент на водиле.
Рис. 36. Сложный зубчатый механизм 5. Рассматриваем равновесие колес 1-2 планетарного редуктора, 6. Рассматриваем равновесие блока сателлитов 2 - 2', 7. Рассматриваем равновесие одной ветви водила Н, определяем 8. Проверка правильности силового расчета. Момент на валу водила Мн, определенный по пункту 4,должен быть равен Мн, определенный по пункту 7. 9. После пункта 3 силовой расчет можно начинать с ""С расчетный = Мс заданный Задания на контрольную работу Студенты третьего курса специальности 160901 заочного обучения по дисциплине «Теория механизмов и машин» выполняют одну контрольную работу на тему «Исследование сложного зубчатого механизма». При выполнении контрольной работы должны быть соблюдены следующие требования: 1. Контрольная работа должна строго соответствовать выбранному варианту. 2. Графическая часть работы аккуратно выполняется на листе формата АЗ или на листе миллиметровой бумаги (кроме синей) формата АЗ. 3. Пояснительная записка пишется четким почерком на листах формата А4. Решение должно сопровождаться краткими, ясными пояснениями, ссылками на применяемые законы и уравнения, изложение допускается вести в безличной форме. Формулы, встречающиеся в пояснительной записке, должны быть расположены отдельными строками. Структура титульного листа пояснительной записки приведена ниже. 4. Вычисление следует производить с точностью до двух значащих цифр после запятой. 5. Перед решением задачи в пояснительной записке записываются ее условия с числовыми данными, вычерчивается схема механизма без масштаба. На листе формата АЗ все чертежи выполняются в масштабе.
1. Определить тип редуктора, его применимость. 2. Аналитически и графически определить передаточное отношение редуктора. 3. Определить основные характеристики планетарного редуктора, исходя из условий сборки, соседства, соосности (если в схеме планетарных редукторов больше одного - то основные характеристики выполнить для каждого планетарного редуктора). Число сателлитов «р» выбрать, исходя из величины передаточного отношения. 4. Выполнить силовой расчет редуктора. Считать колеса редуктора нулевыми. Модули колес принять равными т = 1 мм. или т = 1,5 мм. или т = 2 мм. План зубчатого механизма вычертить в масштабе. 5. Осуществить проверку правильности выполнения силового {Мвх-сдвх = Мвых -СОёых) при /I =1, где ^ - коэффициент полезного действия редуктора. 6. Определить коэффициент полезного действия (КПД) редуктора. 7. Определить мощность и число оборотов двигателя. 8. В общем виде вычертить схему привода кривошипно -шатунного механизма (КШМ), определив и обозначив кинематические и силовые характеристики на каждом валу схемы. Во время экзаменационной сессии студент выполняет лабораторную работу, защищает проверенную преподавателем контрольную работу, сдает дифференцированный зачет по всему курсу, содержание которого представлено на страницах 4-6 данного пособия. Номер задания студент выбирает по приведенной ниже таблице 2 в соответствии с первой буквой своей фамилии. Таблица 2
I 4. Пример выполнения контрольной работы Исходные данные: схема зубчатого механизма (рис. 37), числа зубьев колес 21 =80 22 = 30 23 = 20 2, = 16 25 = 16 23' = 48. Направление вращения тихоходного вала на выходе редуктора (вала водила Н2) - по часовой стрелке, (л)цг.~ 14,13 с"1; что соответствует /г,^ = 135 об/мин. Момент сопротивления на тихоходном (выходном) валу редуктора М„2 = Мс = 100 нм. Определить: провести исследование сложного зубчатого механизма. 1. Определить тип редуктора. Данный редуктор - сложный планетарный механизм, состоит из двух планетарных редукторов, т.к. в каждом редукторе есть солнечное колесо (1 и 4), сателлиты (2 и 5), опорные колеса (3 и 3) и водила (Н1 и Н2). Первая ступень - редуктор Джемса, вторая ступень - тоже редуктор Джемса, Сочетание этих двух редукторов может быть применено в силовой быстроходной передаче.
2. Аналитически и графически определить передаточное
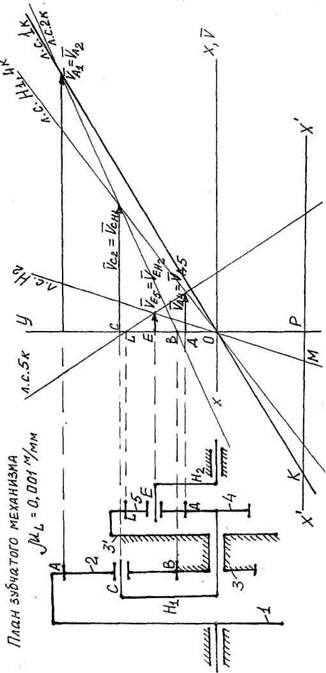
а) Аналитически: ".«.=1-«»,, = 1-^— -—1 = 1+— = 1 + |? = 1 + 0,25 = 1,25; 4Нг ° [ 24 2Ь\ 2, 16 И|Я2 =1,25-4 = 5. б) Графически: Чертим план зубчатого механизма. Выбираем модуль колес, принимаем т = 1,5 мм и определяем размеры колес для зубчатого механизма. г, = 80; </, = т%, = 1,5 • 80 = 120мм \ г, = 0,06.и; г2 = 30; с12 = /и2, = 1,5 • 30 = 45мм; г, = 0,0225.м \ 2Э=20; (/3=/и2з=1,5-20 = 30.ш<; г3=0,015.«; 2„=1б; (/4=ш24=1,5 16 = 24л(.и; г, =0,012.«; г ,=48; 1/,=т2,=1,5-48 = 72д|.и; л=0,036.и; Ззз з г5=1б; ^5=т25 =1,5-16 = 24.1ш; /-5=0,012л*. Тогда А =——— =-7-г-= 0,001 м/мм. гогда ^ «, РА(герт) 60 Для вычерченного в масштабе зубчатого механизма строим план скоростей (рис. 38). Выбираем систему координат УОХ, в которой откладываем произвольный вектор скорости точки А колеса 1-1^^, через конец вектора Щц и точку О проводим линию скоростей 1 колеса (л.с. 1 к). В точке А Ци* ?Аг. %% - вектор окружной скорости сателлита 2. В точке «В» находится мгновенный центр скоростей сателлита 2, через конец вектора и точку «В» проведем линию скоростей сателлита (л.с. 2 к). В точке „С скорость сателлита 2 и скорость водила Н, совпадают, проведем из точки С вектор 7сг = %щ Д° пересечения с линией скоростей сателлита. Через конец вектора УСщ и точку О проведем линию скоростей водила (л.с. Н,), которая является одновременно линией скоростей колеса 4, оо Ц ■4! Найдем на этой линии скорость точки Д колеса 4 - у,и = Уд5. Колесо 5 - сателлит, мгновенный центр скоростей которого находится в точке I, поэтому через конец вектора скорости точки Д4 и точку Ь проведем л.с.бк - сателлита 5. В точке Е скорость колеса 5 - сателлита и водила Н2 совпадают Ур.ь=Уе.нг, поэтому из точки Е проведем вектор скорости до пересечения с л.с.бк, получим вектор скорости водила уЕ„2 , через конец вектора уЕн2 и точку О проведем л.с.Н2.Ллан скоростей построен. Для определения передаточного отношения на произвольном расстоянии ОР параллельно оси х - х проводим линию х' - х' , которая пересекает л.с.1к в точке К и л.с.Н2 - в точке М. Передаточное отношение и» МР \\,5мм Знак передаточного отношения положительный - отрезки КР и МР лежат в одной четверти. 3. Определить основные характеристики редуктора: а) условие сборки: - для редуктора 1 — 2 — 3 — Н1 г,+гг=кр; 80+20 = 254. Берем 4 сателлита, в этом случае условие сборки соблюдается. - для редуктора 4 - 5 - 3' - Н2 г,+2г,=КР; 16 + 48 = 16-4, р = 4, в этом случае условие сборки соблюдается. б) условие соседства: - для редуктора 1-2-3 -НЬ 1. (г, -г2Ут7Г/р^.22+2 - внутреннее зацепление (80-30)5т180°/4 >30+2 50-0,71 > 32 - условие соблюдается. 2. (22+г3)зтж/р^г2+2 (30 + 20)зт180°/4 > 30+2 500,71 > 32- условие соблюдается. - для редуктора 4 - 5 - 3' - Н2 1. \2,-г5)вт7Г/р^г$+2 - внутреннеезацепление (48-1б)ып180'74 > 16+2 320,71 > 18 - условие соблюдается. 2. (г, + 25)8шл/р>25 +2 -внешнеезацепление 320,71 > 18 - условие соблюдается. в) условие соосности: - для редуктора 1—2-3 -Н! 2) + 22 = 2, — 22 20 + 30 = 80-30 50 = 50 - условие соблюдается. - для редуктора 4 - 5 - 3'- Н2 - 7и + 25 = 2з< - 2-5 или 16 + 16 = 48 - 16; 32 = 32 - условие соблюдается. Таким образом, условия сборки, соседства и соосности для обеих зубчатых механизмов (редукторов) соблюдаются при р = 4. 4. Выполним силовой расчет редуктора. Силовой расчет редуктора заключается в определении усилий в зацеплениях, усилий на валах и усилий в подшипниках водила. Силовой расчет проводим без учета КПД редуктора, т.е. при ф, *' 1. а) Вычерчиваем в масштабе план сложного зубчатого механизма (рис. 39). Предположим, направление вращения водила Н2 - по часовой стрелке (отмечаем на чертеже, рис. 39), тогда направление момента сопротивления Мс на валу водила Н2 - в противоположную сторону (момент сопротивления всегда направлен в сторону, противоположную направлению со , в данном случае (л)нг )■ Знак передаточного отношения зубчатого механизма положительный, значит направление вращения вала на входе в редуктор (00^ ) совпадает с направлением вращения вала ведомого водила (СОщ )• направление вращения вала колеса 1 отмечаем на чертеже, рис. 39. Направление движущего момента (Мд - на валу колеса 1) всегда совпадает с направлением вращения ведущего колеса (отмечаем направление Мэ на чертеже, рис.39). б) Определяем СОх и Мэ на входе в редуктор м ,00 Ш& *й)4 ъШщг&шж* 14,13-5= 70,65 6"'; Мвх= Мд=^-=-т?-20нм. в) Силовой расчет планетарного редуктора - нужно всегда 1. В масштабе^ = -—;—\=^~ = 0,0015 м/мм вычерчиваем план колес 1-2 (рис.40). В редукторе 1-2-3-Н! имеется четыре симметрично расположенных сателлита, поэтому движущий момент равномерно распределяется между всеми сателлитами. Расчет ведется по одному сателлиту, поэтому М$ - -Ц& - 4г - &нм- Силы взаимодействия колес 1 и 2 приложены в точке Р (полюс зацепления) и направлены по нормали к профилям зубьев (по линии зацепления ММ), угол зацеплениям^ 20. Сила Р12 сила реакции со стороны ведущего колеса 1 на ведомое колесо 2. Сила Р21 - сила реакции со стороны ведомого колеса 2 на ведущее колесо 1.
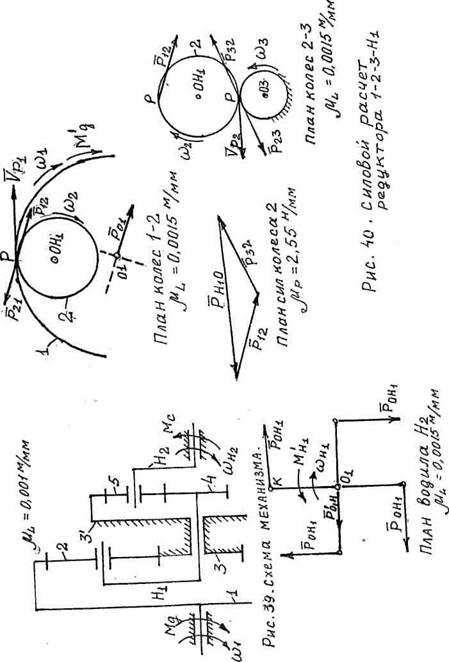
Положение нормали NN определяется правилом: если ведущим является колесо с внутренним зацеплением, то поворачивая вектор окружной скорости уР, на угол сс0 (а0=20°) по направлению угловой скорости ведущего колеса, получим положение нормали N - N и вектор силы реакции ведущего колеса на ведомое (?|2). Вектор ?21 = -?12. Рассматриваем равновесие колеса 1. Колесо 1 находится в равновесии под действием силы ~ри, момента м\ и реакции на валу Лн. 3>0,(?)=о, Р21-А-Л^=0 м\ А = —'-; к = к • сов 20° = 0,06 • 0,94 = 0,056л<; />"= в=89'3"; Ря = ~ла''" = 89,зм ■ />21 + Яш = 0; Ргх = -Рт , Р01 = 89,3н. 2. В масштабе 0,0015 м/м вычерчиваем план колес 2-3 (рис. 4#). В точке Р определяем положение нормали NN по правилу: если ведущим является колесо с внешним зацеплением (колесо 2), то поворачивая вектор окружной скорости точки Р уп на угол а„ (аш =20°) против направления вращения угловой скорости ведущего колеса а>г, получим положение нормали N - N и вектор силы реакции ведущего колеса на ведомое (здесь условно ведомое колесо 3) ?23, ?и = -?32. Рассматриваем равновесие колеса 2 (сателлита) Здесь а, = й2 =г2 -сова, значит|А32|=|;;2|. и р32 =89,зя. Графически решаем это уравнение, т.е. строим план сил, который должен быть замкнут (рис. 63). 89 3 Масштаб плана сил цР = -—=- = 2,55н/лш. ^' 35 Рн„=Рн,о р,е =65-2,55 = 165,75», Р =-Р г Я,0 ' ОН, '
3. В масштабе 0,0015 м/мм строим план водила (четыре ветви). ОгК = г2+г} = 0,0225м + 0,015м = 0,0375м. О 0175 На чертеже о.к = '±^± = гъмм. г ' 0,0015 Рассматриваем равновесие одной ветви водила. Одна ветвь водила находится в равновесии под действием силыр()Я , м'н и рон. м'н = рон, ■ 0,К = 165,75н-0,0375м = 6,21нм. ^]? = 0, Рон, +~Ро,н =0, Р~он, =-Рохн, Рон, = 165,75н. Как видно из чертежа, каждая ветвь водила имеет реакцию со стороны вала ?0,« = Ш,75», и суммарная реакция со стороны вала равна нулю, значит вал водила уравновешен. Для остальных ветвей водила расчет тот же, поэтому момент на Валу ВОДИЛа Н, равен М„ = м'„ 4 = 6,21-4 = 24,84км. Этот же момент действует на валу колеса 4, т.е. м„ =мн и со„ = сол. 4. Проводим силовой расчет редуктора 4 - 3' - 5' - Н2, рис. 4 т. является ведомым, а колесо 4 для редуктора 4 - 5 - 3' - Н2 ведущим, поэтому направление вращения со, (по часовой стрелке) совпадает с направлением момента м„. - В масштабе ц1 =о,оо\м1мм вычерчиваем план колес 4-5, отметим, колесо 4 - ведущее, колесо 5 - сателлит - ведомое. Рассмотрим равновесие колеса 4. В редукторе четыре симметрично расположенных сателлита, поэтому М4=л/,/4=24,84/4 = б,21нл<. Колесо 4 находится в равновесии под действием силы я», момента м\ и силы ?<м. 5>„(р)=°. Р»к-м\=о, Л = г4со820° = 0,012-0,94 = 0,0113^, ^=^ = -^_ = 549,55„, Н 0,0113 Л* =-/"«. Л5=549,55н. 1?=_о, Р»+Р04=0, Р54=-Р„, /> =549,55н. Рис. И Силовой расчет { рЕДУНТООА ^-5-3 ~Н2.
Рассматриваем равновесие колеса 5 - сателлита. Сателлит 5 находится в равновесии под действием сил р3'5, ?« и силы действия водила Н2 на сателлит 5 р~н2о . 2>„(?)=о, р„ь,-р,;Н,=о, Р, = р = 549,55н. 3 5 45 ' , /5з,5+Р45 + Ря2о = о, решаем это уравнение графически. Строим план сил в масштабе/^ =—— = 18,з«/лш и определяем р„10, РИг0 ттф, = 6018,3 = 1098н. - В масштабе //, =ШИ= водила Н2 (4 ветви). Рассмотрим равновесие одной ветви водила. Ветвь водила находится в равновесии под действием сил рон , р'он и момента м'„ . 2>.(?)=о, м'Н1-рон^н = о, й = 0,024-сое 20°, Л^, = 1098 • 0,024 • 0,94 =24,77™. Для остальных ветвей водила расчет тот же, поэтому момент на валу водила Н2 равен М„ =МН ■4 = 24,77-4 = 99,0&нм*100нм. н2 нг Отметим направление момента м„ , угловая скорость совпадает с направлением момента и угловой скорости на выходе из редуктора, определенного по заданному направлению угловой скорости. Проверяем правильность расчетов. Составим уравнение мощности на входе и выходе редуктора (энергетическое равенство), М1Фх=МнСОн, при УСЛОВИИ 77 = 1. М,ЦН2=МН2. 20нм ■ 5 = Шнм. В расчете получили мнг =99,08км. Процент ошибки 0,9 %. Расчет проведен верно. 5. Определяем КПД редуктора. Ч\Нг =Ч\ИХ 'Ч4Нг ■ ^ш,=^-[1-?7'(1-",я)]. ищ =1,25; 77'=0,95 •0,95 = 0,9, 7.я, =^[1-0,9(1-1,25)1=0,98, Чщ =7Г-[1-;7'(1-",«)]=1[1-0.9(1-4)] = 0,92, И4Н2 4 Цщ =0,98 0,92 = 0,9. 6. Определяем мощность на выходе из редуктора, мощность на - мощность на выходе из редуктора равна мощности Яъш^Фщшт, -Му,, = 14,13100 = 1413вт Значит мощность на выходе из редуктора л^ =1413вот. - мощность на входе в редуктор определим с учетом КПД, 77 °'у - мощность двигателя совпадает с мощностью на входе в Число оборотов двигателя равно числу оборотов на валу входа в родуктор. по, =п«.р. *Л«й..>Ц»1 =135-5 = 675об/л<ин. 7. Вычерчиваем схему привода КШМ с учетом направления
|
Рис. 24. План скоростей и план чисел оборотов планетарного механизма
2.4.3. Сложные планетарные механизмы
52
20 + 36 = 2,-36, 23=92.
2.4.6. Силовой расчет зубчатых механизмов
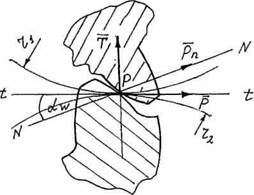
2. Если ведущим колесом является колесо с внутренним зацеплением (рис. 31). то вектор скорости точки касания нужно поворачивать по направлению угловой скорости ведущего колеса.
Определим положение линии N - N. повернув вектор окружной скорости \А^против вращения й?,. Колесо 3 находится в равновесии под
Силовой расчет сложного планетарного редуктора проводится по кинематической схеме редуктора. Каждая схема редуктора имеет свой алгоритм силового расчета.
При решении задачи необходимо выполнить:
