 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Сила Кориолиса и закон сохранения момента импульса
Если вращающаяся лаборатория, принимаемая за неинерциальную систему отсчёта, имеет конечный момент инерции, то в соответствии с законом сохранения момента импульса при движении тела по радиусу, перпендикулярному оси вращения, угловая скорость вращения будет увеличиваться (при движении тела к центру) или уменьшаться (при движении тела от центра). Рассмотрим эту ситуацию с точки зрения неинерциальной системы. Хорошим примером может быть человек, который перемещается в радиальном направлении по вращающейся карусели (например, держась за ведущий к центру поручень). При этом с точки зрения человека он при движении к центру будет совершать работу против центробежной силы (эта работа пойдёт на увеличение энергии вращения карусели). На него также будет действовать сила Кориолиса, которая стремится отклонить его движение от радиального направления («сносит» его вбок), и противодействуя сносу (прилагая поперечное усилие к поручню), он будет раскручивать карусель. При движении от центра центробежная сила будет совершать работу над человеком (за счёт уменьшения энергии вращения), а противодействие силе Кориолиса будет тормозить карусель. 9) Тре́ние — процесс взаимодействия тел при их относительном движении (смещении) либо при движении тела в газообразной или жидкой среде. По-другому называется фрикционным взаимодействием . Изучением процессов трения занимается раздел физики, который называется механикой фрикционного взаимодействия, или трибологией Сила трения Сила трения — это сила, возникающая в месте соприкосновения тел и препятствующая их относительному движению. Причины возникновения силы трения: 1) Шероховатость соприкасающихся поверхностей. 2) Взаимное притяжение молекул этих поверхностей. Сила трения прямо пропорциональна весу тела (P) и силе нормальной реакции (N) и зависит от того, насколько сильно тела прижаты друг к другу. Виды При наличии относительного движения двух контактирующих тел силы трения, возникающие при их взаимодействии, можно подразделить на: · Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения. · Трение качения— момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого. · Трение покоя— сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения. В физике взаимодействия трение принято разделять на: · сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками (в том числе и твердыми смазочными материалами) — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя; · граничное, когда в области контакта могут содержаться слои и участки различной природы (окисные плёнки, жидкость и так далее) — наиболее распространённый случай при трении скольжения. · смешанное, когда область контакта содержит участки сухого и жидкостного трения; · жидкостное (вязкое), при взаимодействии тел, разделённых слоем твёрдого тела (порошком графита), жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость, величина вязкого трения характеризуется вязкостью среды; · эластогидродинамическое (вязкоупругое), когда решающее значение имеет внутреннее трение в смазывающем материале. Возникает при увеличении относительных скоростей перемещения. В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики Ламинарный поток. Обычно ламинарный поток возникает, когда жидкость течет по маленькой трубе и / или с маленькой скоростью. Он может рассматриваться как серия жидких цилиндров в трубе, и тем быстрее течет цилиндр, чем он ближе к внутреннему (оси трубы), а цилиндр, соприкасающийся с трубой, неподвижен. Профиль распределения скоростей зависит практически только от вязкости жидкости - u - и не зависит от плотности - ρ. Турбулентный поток. Большие и маленькие водовороты и завихрения делают турбулентный поток непредсказуемым. Он возникает при большой скорости жидкости. Профиль рапределения скоростей в таком потоке - функция, зависящая от плотности - ρ.
Турбуле́нтность, устар. турбуле́нция , турбуле́нтное тече́ние — явление, заключающееся в том, что при увеличении скорости течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности. Волны появляются случайно. То есть их размер и амплитуда меняется хаотически в некотором интервале. Они возникают чаще всего либо на границе, у стенки, и/или при разрушении или опрокидывании волны. Они могут образоваться на струях. Экспериментально ее можно наблюдать на конце струи пара из электрочайника. Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой жидкости (воды) в трубах. 11) Закон (уравнение) Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
Здесь
В научной литературе закон Бернулли, как правило, называется уравнением Бернулли[1](не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли[2][3] или интегралом Бернулли[4][5]. Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока. Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления (см. приводимый в приложении вывод уравнения Бернулли) и не представляет собой запаса какого-либо специального вида энергии («энергии давления»[6]). Соотношение, близкое[7] к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года. Для горизонтальной трубы Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока. Полное давление состоит из весового Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (напримертруба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики. Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях. 12)Ввв 13) Постулат 1 (принцип относительности Эйнштейна). Любое физическое явление протекает одинаково во всех инерциальных системах отсчёта. Это означает, что форма зависимости физических законов от пространственно-временных координат должна быть одинаковой во всех ИСО, то есть законы инвариантны относительно переходов между ИСО. Принцип относительности устанавливает равноправие всех ИСО. Учитывая второй закон Ньютона (или уравнения Эйлера-Лагранжа в лагранжевой механике) можно утверждать, что если скорость некоторого тела в данной ИСО постоянна (ускорение равно нулю), то она должна быть постоянна и во всех остальных ИСО. Иногда это и принимают за определение ИСО. Формально, принцип относительности Эйнштейна распространил классический принцип относительности (Галилея) с механических на все физические явления. Однако, если учесть, что во времена Галилея физика заключалась собственно в механике, то и классический принцип тоже можно считать распространяющимся на все физические явления. В том числе он должен распространятся и на электромагнитные явления, описываемые уравнениями Максвелла. Однако, согласно последним (и это можно считать эмпирически установленным, так как уравнения выведены из эмпирически выявленных закономерностей), скорость распространения света является определённой величиной, не зависящей от скорости источника (по крайней мере в одной системе отсчёта). Принцип относительности в таком случае говорит, что она не должна зависеть от скорости источника во всех ИСО в силу их равноправности. А значит, она должна быть постоянной во всех ИСО. В этом заключается суть второго постулата: Постулат 2 (принцип постоянства скорости света). Скорость света в «покоящейся» системе отсчёта не зависит от скорости источника. Поскольку источник имеет разные скорости в разных ИСО, то это означает, что скорость света одинакова во всех инерциальных системах. Принцип постоянства скорости света противоречит классической механике, а конкретно - закону сложения скоростей. При выводе последнего используется только принцип относительности Галилея и неявное допущение одинаковости времени во всех ИСО. Таким образом, из справедливости второго постулата следует, что время должно быть относительным - неодинаковым в разных ИСО. Необходимым образом отсюда следует и то, что "расстояния" также должны быть относительны. В самом деле, если свет проходит расстояние между двумя точками за некоторое время, а в другой системе - за другое время и притом с той же скоростью, то отсюда непосредственно следует, что и расстояние в этой системе должно отличаться. Необходимо отметить, что световые сигналы, вообще говоря, не требуются при обосновании СТО. Хотя неинвариантность уравнений Максвелла относительно преобразований Галилея привела к построению СТО, последняя имеет более общий характер и применима ко всем видам взаимодействий и физических процессов. Фундаментальная константа В связи с этим второй постулат следует формулировать как существование предельной (максимальной) скорости движения. По своей сути она должна быть одинаковой во всех ИСО, хотя бы потому, что в противном случае различные ИСО не будут равноправны, что противоречит принципу относительности. Более того, исходя из принципа "минимальности" аксиом, можно сформулировать второй постулат просто как существование некоторой скорости, одинаковой во всех ИСО, а после вывода соответствующих преобразований - показать, что это предельная скорость (потому, что подстановка в эти формулы скоростей больше этой скорости приводит к мнимости координат). 14)Пусть координатные оси двух инерциальных систем отсчёта Общий вид преобразований Лоренца в векторном виде [13], когда скорость систем отсчёта имеет произвольное направление:
где Если сориентировать координатные оси по направлению относительного движения инерциальных систем (то есть в общие формулы подставить
где
Подобный предельный переход является отражением принципа соответствия, согласно которому более общая теория (СТО) имеет своим предельным случаем менее общую теорию (в данном случае — классическую механику). Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и скорости при переходе от одной инерциальной системы отсчета (ИСО) к другой. Термин был предложен Филиппом Франком в 1909 году. Преобразования Галилея опираются на принцип относительности Галилея, который подразумевает одинаковость времени во всех системах отсчета («абсолютное время»). Достаточно продифференцировать
Рассмотрим преобразование произвольного сдвига начала отсчета на вектор где радиус-вектор какого-то тела A в системе отсчета K обозначим за подразумевая, как всегда в классической механике, что время Тогда в любой момент времени
и в частности, учитывая
имеем:
где:
Если
или короче
— как для средних, так и для мгновенных скоростей (формула сложения скоростей). Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга:
15)Отсюда вытекает:
И, аналогично:
Если тело движется только вдоль оси X:
Пусть u'=c, тогда:
Т.е. вытекает постоянство скорости света в разных системах отсчета. Теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Правило сложение скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:
Можно заметить, что в случае, когда 16) Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
или ,
Обобщенное гармоническое колебание в дифференциальном виде
17)Пп 18) Резона́нс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн. 19) Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёнымЖюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или |




 — плотность жидкости,
— плотность жидкости, — скорость потока,
— скорость потока, — высота, на которой находится рассматриваемый элемент жидкости,
— высота, на которой находится рассматриваемый элемент жидкости, — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости, — ускорение свободного падения.
— ускорение свободного падения. и уравнение Бернулли принимает вид:
и уравнение Бернулли принимает вид:  .
.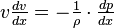 .
.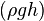 , статического
, статического  и динамического
и динамического  давлений.
давлений. , возникающая в преобразованиях Лоренца, имеет смысл предельной скорости движения материальных тел. Численно она совпадает со скоростью света, однако этот факт, согласно современной квантовой теории поля (уравнения которой изначально строятся как релятивистски инвариантные) связан с безмассовостью электромагнитных полей. Даже если бы фотон имел отличную от нуля массу, преобразования Лоренца от этого бы не изменились. Поэтому имеет смысл различать фундаментальную скорость
, возникающая в преобразованиях Лоренца, имеет смысл предельной скорости движения материальных тел. Численно она совпадает со скоростью света, однако этот факт, согласно современной квантовой теории поля (уравнения которой изначально строятся как релятивистски инвариантные) связан с безмассовостью электромагнитных полей. Даже если бы фотон имел отличную от нуля массу, преобразования Лоренца от этого бы не изменились. Поэтому имеет смысл различать фундаментальную скорость  [8]. Первая константа отражает общие свойства пространства и времени, тогда как вторая связана со свойствами конкретного взаимодействия.
[8]. Первая константа отражает общие свойства пространства и времени, тогда как вторая связана со свойствами конкретного взаимодействия. и
и  параллельны друг другу,
параллельны друг другу,  — время и координаты некоторого события, наблюдаемого относительно системы
— время и координаты некоторого события, наблюдаемого относительно системы  — время и координаты того же события относительно системы
— время и координаты того же события относительно системы 
 — фактор Лоренца,
— фактор Лоренца,  и
и  — радиус-векторы события относительно систем S и S'.
— радиус-векторы события относительно систем S и S'. ) и выбрать это направление в качестве оси
) и выбрать это направление в качестве оси  (то есть так, чтобы система S' двигалась равномерно и прямолинейно со скоростью
(то есть так, чтобы система S' двигалась равномерно и прямолинейно со скоростью 
 ) преобразования Лоренца переходят в преобразования Галилея:
) преобразования Лоренца переходят в преобразования Галилея:
 в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости.
в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости. ,
, ,
, в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени:
в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени:  .
.
 ,
,

 — средняя скорость тела A относительно системы K;
— средняя скорость тела A относительно системы K; — средняя скорость тела А относительно системы K' ;
— средняя скорость тела А относительно системы K' ; — средняя скорость системы K' относительно системы K.
— средняя скорость системы K' относительно системы K.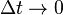 то средние скорости совпадают с мгновенными:
то средние скорости совпадают с мгновенными:





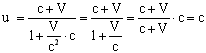
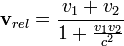
 , преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом сочетаются эти две теории — первая является уточнением второй.
, преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом сочетаются эти две теории — первая является уточнением второй.
 где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд;
где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд;  — полная фаза колебаний,
— полная фаза колебаний,  — начальная фаза колебаний.
— начальная фаза колебаний. (Любое нетривиальное[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой
(Любое нетривиальное[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой  )
) вырождаются в отрезки прямых, а при разности фаз
вырождаются в отрезки прямых, а при разности фаз  и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.
и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.