 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задача №4. Схемные функции линейных электрических цепей.
Задача №3. Переходные процессы в линейных электрических цепях. Дана электрическая, в которой происходит коммутация(рис.3.1-3.10). В цепи действует постоянная ЭДС Е. Параметры цепи даны в таблице 3. Определить закон изменения во времени тока после коммутации в одной из ветвей схемы или напряжения на каком-либо элементе или между заданными точками схемы. Задачу следует решить двумя методами: классическим и операторным. На основании полученного аналитического выражения построить график изменения искомой величины в функции времени на интервале от t=0 до t/|p|мин. Здесь |p|мин – меньший по модулю корень характеристического уравнения.
Решение классическим методом. В классическом методе расчета переходных процессов решение дифференциального уравнения представляет собой сумму принужденной и свободной составляющей:
Рассчитаем режим до коммутации – t(0_). К началу переходного процесса непосредственно перед коммутацией все токи и напряжения на пассивных элементах равны нулю:
Т.е. имеются место нулевые независимые начальные условия.
Заменим параллельно соединенные сопротивления R1 и R2 эквивалентным сопротивлением:
Составляем характеристическое уравнение для данной схемы:
Отсюда следует, что характеристическое уравнение будет иметь вторую степень после замены в выражении Z(p):
Для того, чтобы определить принужденную составляющую, рассмотрим установившийся процесс после коммутации:
По независимым начальным условиям рассчитаем напряжение на емкости Запишем уравнение для определения
Дифференцируем и подставим время t=0;
Определим постоянные интегрирования А1 и А2:
Запишем переходное напряжение
Решение операторным методом. В случае из плоскости оригиналов переходят в плоскость изображения по Лапласу:
Найдем ток
Для перехода от изображения к оригиналу воспользуемся общей теоремой разложения для случайных простых корней:
Найдем корни уравнений
Отсюда следует:
Получаем следующий результат:
Результаты расчета тока совпали с данными, полученными классическим методом. Построим график изменения тока
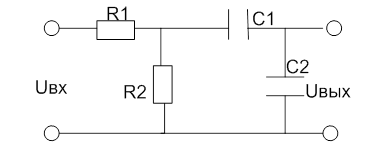
Задача №4. Схемные функции линейных электрических цепей. Найти схемные функции: КU(p) , КU(jω) , КU(ω) , IU(ω) , h(t). Представить временную диаграмму работы схемы, если на её вход поступает последовательность прямоугольных импульсов с амплитудой Um, периодом Т и скважностью q.
Для последующего решения данного задания необходимо указать направления токов в ветвях и составить систему уравнений, описывающих токи в данной схеме:
Для узлов а и б составим уравнения по первому закону Кирхгофа:
Совместив две системы уравнений получим:
Данную систему уравнений можно перевести в операторную форму, т.к.
Для нахождения коэффициента передачи следует исключить вспомогательную переменную UR2. Из второго уравнения получаем:
Подставляем полученное уравнение в первое уравнение системы:
Определяем коэффициент передачи:
Выражаем комплексный частотный коэффициент передачи, выполняя замену переменной
Найдем фазочастотную характеристику (ФЧХ).
По полученным аналитическим выражениям для АЧХ и ФЧХ строим в логарифмическом масштабе соответствующие характеристики:
После преобразование получаем:
Кривые
Графики
Из анализа ЛАЧХ и ФЧХ следует, что с точки зрения передачи гармонических сигналов схема является фильтром низких частот. Определим изображение H(p)
Анализ работы схемы при передаче последовательности прямоугольных импульсов.
2.
3. 4. Таким образом, можно отметить, что прямоугольный импульс, проходя через данную схему изменяется по форме и длительности. Следует так же отметить, что если постоянная времени фильтра намного меньше входного импульса, то цепь практически без искажения передает прямоугольный сигнал.
|
Корни характеристического уравнения вещественные и различные – переходный процесс апериодический.
при t(0+), а затем тока 
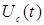и найдем переходной ток 
с помощью уравнений составленных по законам Кирхгофа:
в интервале от t=0 до t=3/|pmin|=3/5000=0.6 мс.
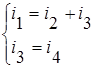
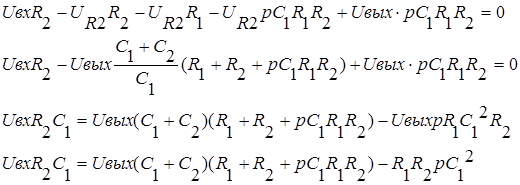
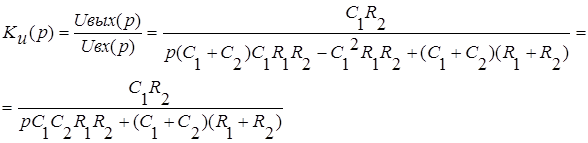
и получили AЧХ.
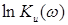и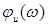 
, построенные в логарифмическом масштабе частот
, соответственно называются логарифмической амплитудной (ЛАЧХ) и фазовой (ЛФЧХ) частотными характеристиками.
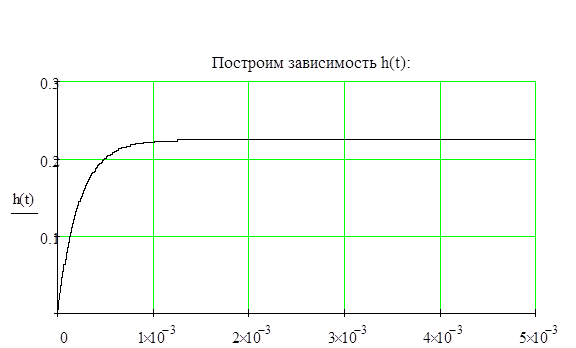
1. 
