ПОЗНАВАТЕЛЬНОЕ

Сила воли ведет к действию, а позитивные действия формируют позитивное отношение

Как определить диапазон голоса - ваш вокал

Игровые автоматы с быстрым выводом

Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими

Целительная привычка

Как самому избавиться от обидчивости

Противоречивые взгляды на качества, присущие мужчинам

Тренинг уверенности в себе

Вкуснейший "Салат из свеклы с чесноком"

Натюрморт и его изобразительные возможности

Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.

Как научиться брать на себя ответственность

Зачем нужны границы в отношениях с детьми?

Световозвращающие элементы на детской одежде

Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия

Как слышать голос Бога

Классификация ожирения по ИМТ (ВОЗ)

Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Проверка критерия погоды по диаграмме статической остойчивости. Вычисление площадей а и b.

Оглавление

1.

Целями работы являются:

1). Определение посадки и начальной остойчивости судна при расчетной весовой нагрузке.

2). Проверка соответствия остойчивости судна при расчетной весовой нагрузке требованиям правилам Российского Морского Регистра Судоходства.

Сведения о расчетной весовой нагрузке приведены в пункте

Исходные данные

2. Теоретический чертеж судна представлен на рис. 1 и рис. 2 соответственно.

3. Исходные данные для построения кривых элементов теоретического чертежа даны в табл.1 и табл. 2.

4. Исходные данные для построения интерполяционных кривых плеч остойчивости формы l_фк (от киля) представлены в табл. 3.

Рис. 1. Теоретический чертеж

Рис. 2. Схема расстановки сечений

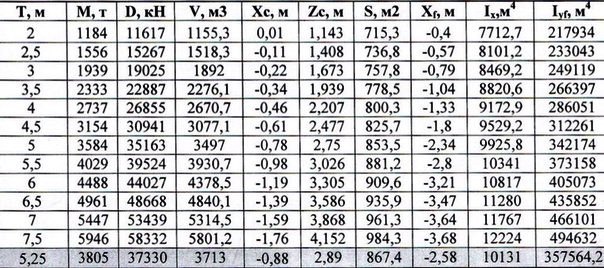
Табл. 1

Табл. 2

где:

Т –средняя осадка;

V – объемное водоизмещение;

Z_c – аппликата центра величины;

r₀ – поперечный метацентрический радиус;

Z_mВ – аппликата метацентра;

R₀ – продольный метацентрический радиус;

S – площадь действующей ватерлинии;

х_c – абсцисса центра величины;

х_f – абсцисса центра тяжести площади ватерлинии;

М – массовое водоизмещение;

D – весовое водоизмещение;

Ω – площадь смоченной поверхности судна;

δ – коэффициент общей полноты;

α – коэффициент полноты ватерлинии;

β – коэффициент полноты мидель-шпангоута;

A_v – площадь парусности, т.е. площадь проекции надводной части судна без хода на тихой воде на ДП;

Z_п – аппликата центра парусности.

Табл. 3.

3.

Для построения гидростатических кривых воспользуется данными из табл. 1 и табл. 2. Результаты работы представлены на рис. 3 и рис. 4. Принятые на рисунках обозначения расшифрованы на страницах 7-8 и их масштаб приведен в табл. 4.

Табл. 4

4.

Исходные величины, необходимые для построения пантокарен приведены в таблице 3. Результаты работы представлены на рис. 5 и рис.6.

l_фк, м – плечо остойчивости формы от киля

M, т – массовое водоизмещение

Все расчеты приведены в табл. 5.

	Начальная поперечная метацентрическая высота	м	h0 = r0 + zc – zg	0,5
	Поправка к метацентрической высоте	м	δh = iжi · ρ жi)/М
	Исправленная поперечная метацентрическая высота	м	h = h0 + δh	0,5
	Продольная начальная метацентрическая высота	м	H0 = R0 + zc – zg	96,1
	Угол дифферента	радиан	Ψ = (xg – xc) / H0
	Осадка носом	м	Тн = Т + (L⊥⊥/2 – xf) · Ψ	4,9
	Осадка кормой	м	Тк = Т – (L⊥⊥/2 + xf) · Ψ	4,9
	Число тонн осадки на 1 см	т/см	q = 0,01·S·ρ	8,71
	Момент кренящий на 1 градус	кН*м/градус	mθ =Dh / 57,3	307,1
	Момент дифферентующий на 1 см	кН*м/см	mΨ = 0,01D H0 / L⊥⊥	402,6

Табл. 5

Т.к. Т = 4,9 м, то, пользуясь гидростатическими кривыми снимаем значение x_c, z_c, r₀, R₀, S, X_f

i_жi – момент инерции площади свободной поверхности жидкости, м⁴

ρ_жi – плотность жидкости, имеющей свободную поверхность

В работе принято, что на судне нет наличия свободной поверхности, следовательно, i_жi = 0

Это значит, что δh = 0

6. Построение диаграммы статической остойчивости (ДСО)

Расчетные данные, нужные для того чтобы построить ДСО представлены в табл. 6.

Кривые плеч остойчивости формы взяты из рис. 5, а аппликата центра тяжести из исходных данных. Результаты работы представлены на рис. 7.

Табл.6

где:

θ – угол крена в градусах;

Θ – угол крена в радианах;

sinΘ – синус от угла крена в радианах;

l_фк – плечо остойчивости формы;

l_в – плечо остойчивости веса.

Чтобы построить ДДО, нужно вычислить значение l_d.

Результаты вычислений приведены в табл. 7.

Табл. 7

Диаграмма динамической остойчивости представлена на рис. 8

8.

8.1. Критерий погоды.

Остойчивость судов неограниченного и ограниченных R1, R2, R2-RSN, R2-RSN(4,5)иR3-RSN районов плавания считается по критерию погоды К=b/a достаточной, если площадь b равна или больше площади a, то есть К≥1. При этом:

1. Судно находится под действием ветра постоянной скорости, направленного перпендикулярно к его диаметральной плоскости, которому соответствует плечо ветрового кренящего момента l_w1.

2. От статического угла крена θ_w1, вызванного постоянным ветром и соответствующего первой точке пересечения горизонтальной прямой l_w1 с кривой восстанавливающих плеч l(θ), под действием волн судно кренится на наветренный борт на угол, равный амплитуде бортовой качке θ_1r.

3. На накрененное судно динамически действует порыв ветра, которому соответствует плечо кренящего момента l_w2.

4. Вычисляются и сравниваются площади a и b, заштрихованные на рисунке. Площадь b ограничена кривой l(θ) восстанавливающих плеч, горизонтальной прямой, соответствующей кренящему плечу l_w2, и отрезком от угла θ_с, соответствующем точки первого пересечения кривой l(θ) и прямой l_w2 и углом крена θ_w2 = 50º, либо углом заливания θ_f , либо углом крена θ_с, соответствующего точке второго пересечения прямой l_w2 с кривой восстанавливающих плеч, в зависимости от того, какой из этих углов меньше. Площадь а ограничена кривой восстанавливающих плеч, прямой l_w2 и углом крена, равным θ_w1 - θ_1r.

Графическое изображение проверки остойчивости судна по критерию погоды представлено на рисунке

Ниже представлен расчет плеча кренящего момента от давления ветра l_w1, амплитуды качки θ_1r и угла заливания θ_f .

8.1.1.

Кренящее плечо l_w1, м, принимается постоянным для всех углов крена и рассчитывается по формуле:

l_w1 = p_vA_vz_v/1000gM, где p_v – давление ветра, Па, определяемое в зависимости от района плавания; A_v – площадь парусности, м², определяемая по гидростатическим кривым элементов теоретического чертежа (рис. 4); z_v – плечо парусности, м, принимаемое равным измеренному по вертикали расстоянию от центра площади парусности A_v до центра площади проекции подводной части корпуса на диаметральную плоскость, или, приближенно, до середины осадки судна; М – массовое водоизмещение судна, т; g – ускорение свободного падения, равное 9,81 м/c².

Так как в задаче район плавания неограниченный, то p_v = 504 Па.

A_v = 740 м².

z_v = z_п – z_R, где z_п – аппликата центра парусности; z_R – аппликата центра давления гидродинамической силы на корпусе судна, приближенно равная половине осадки судна.

Z_п = 8.2 м.

Z_R = T/2 = 5.25/2 = 2.62 м.

Z_v = 8.2 – 2.62 = 5.58 м.

М = 3800 т.

Отсюда находим l_w1:

l_w1 = 504·740·5.58/1000·9.81·3800 = 0.05 м.

Кренящее плечо l_w2 определяется по формуле:

l_w2 = 1.5 l_w1

l_w2 = 0.07 м.

Расчет амплитуды качки.

Амплитуда качки с круглой скулой, град., вычисляется по формуле:

Θ_1r = 109kX₁X₂ ,

Где k – коэффициент, учитывающий влияние скуловых и/или брускового килей и определяемый в зависимости от отношения А_k/L_wlB, в котором A_k - суммарная габаритная площадь скуловых килей, м²; l_wl – длина судна по ватерлинии. L_wl = L_⊥⊥ - длина судна между перпендикулярами, м; B – ширина судна. Значение k принимается равным 1, если кили отсутствуют.

X₁ – безразмерный множитель, определяемый в зависимости от отношения ширины к осадке B/T.

X₂ – безразмерный множитель, определяемый в зависимости от коэффициента общей полноты судна С_в.

r – параметр, определяемый по формуле:

r = 0.73+0.6(z_g-T)/T, где z_g – аппликата центра тяжести судна; T – осадка судна.

Значение r не должно приниматься больше 1.

S – безразмерный множитель, определяемый в зависимости от района плавания судна и периода качки судна и периода бортовой качки d, который рассчитывается по формуле:

d = 2cB/ ,

где c = 0.373+0.023B/T - 0.043L_wl/100, в которой h – исправленная метацентрическая высота.

X₁ = 0,96, так как B/T = 2.6

Коэффициент общей полноты снимаем с гидростатических кривых элементо теоретического чертежа (рис.4).

C_в = δ = 0.61

Следовательно X₂ = 0.95

Находим r:

z_g = 5.10 м

T = 5.25 м

r = 0.73+0.6(z_g-T)/T = 0.73+0.6(5.10-5.25)/5.25 = 0.71

Находим S:

Для этого найдет период бортовой качки судна d:

d = 2(0.373+0.023B/T – 0.043L_wl /100)B/

L_wl = L_⊥⊥ = 84.0 м.

B = 13.2 м.

h = 0.40 м.

d = 2(0.373+0.023·2.6 – 0.043·84.0/100)·13.2/ = 16.9 с.

Следовательно S = 0,044

Исходя из данных, рассчитанных выше, находим Θ_1r:

Θ_1r = 109·1·0.96·0.95· = 17.63º ≈ 17º

8.1.3.

Наиболее опасное открытое отверстие – трюмный люк с шириной горловины b = 3,50 м.

Высота комингс люка c = 0,5 м.

tg(θ_f) = BC/OC = 2[(H – T)+c]/b,

где H – высота борта, м;

T – средняя осадка судна, м;

b – ширина горловины трюмного люка, м.

tg(θ_f) = 2[(7.60-5.25)+0.5]/3.50 = 1.62 рад

θ_f = arctg(1.34) = 57.8º

В качестве предельного угла крена выбираем наименьший из трех:

Θ_w2 = 50º; θ_f = 57.8º или угла θ_с, соответствующий точке второго пересечения кривой l(θ) и прямой l_w2. В нашем случае предельным углом крена будет угол Θ_w2 = 50º.

Проверка критерия погоды по диаграмме статической остойчивости. Вычисление площадей а и b.

Находим площадь фигуры а (рис. 9):

a – площадь фигуры, ограниченной прямой l_w2, углом θ_c, соответствующем точке первого пересечения кривой l(θ) и прямой l_w2, кривой l(θ) и углом Θ₀

a = 0,02813 м·рад.

b = S₁ + S₂ + S₃+ S₄, где

S₁ – площадь фигуры, ограниченной прямой l_w2, кривой l(θ) и отрезком с диапазоном от θ_c до угла 10º; S₂ – площадь фигуры, ограниченной прямой l_w2, кривой l(θ) и отрезком длиной от 10º до 40º; ; S3 – площадь фигуры, ограниченной прямой l_w2, кривой l(θ) и отрезком длиной от 40º до 45º; S₄ – площадь фигуры, ограниченной прямой l_w2, кривой l(θ) и отрезком длиной от 45º до 50º;

b = 0.00488 + 0.13298 + 0.04876 + 0.05263 = 0.23925 м·рад.

Остойчивость судна по критерию погоды К=b/a считается достаточной, если площадь b больше или равна площади a, т.е. K≥1

K = 0.23925/0.021813 = 10.968 > 1

Требование к остойчивости по критерию погоды выполняется.

8.1.5.

8.1.6.

b = a + c

а = 0.024 м·рад

с = 0.22 м·рад

См. рис. (10).

b = 0,244 м·рад

а = 0,024 м·рад.

K = b/a = 0.244/0.024 = 10.166 > 1

Требование к остойчивости по критерию погоды выполняется.

8.2.

Статический угол крена θ_w1 от действия постоянного ветра не должен превышать 16º, либо угла, равного 0.8 угла входа в воду кромки открытой палубы, в зависимости от того, какой из них меньше.

θ_w1 = 6º < 16º

Проверка остойчивости судна по статическому углу крена удовлетворяет требованию регистра.

8.3.

Площадь под положительной частью ДСО должна быть не менее 0,055 м·рад до угла крена 30 и не менее 0,09 м·рад до угла крена 40 либо до угла заливания θ_f, в зависимости от того, какой из них меньше. Дополнительно, площадь между углами крена 30 и 40 , или, если θf < 40 , между 30 и θf должна быть не менее 0,03 м·рад.

Площади показаны на рис. 7.

S_m = 0.107 м·рад > 0.055 м·рад

S_m+n = 0.107 + 0.044 = 0.151 м·рад > 0.09 м·рад

S_m-n = 0.107 – 0.044 = 0.063 м·рад > 0.03 м·рад

Диаграмма статической остойчивости полностью соответствует требованиям Морского регистра.

Максимальное плечо диаграммы статической остойчивости L_max должно быть не менее 0.25 м для судов длиной L ≤ 80 м и 0.20 м для судов длиной L ≥ 105 м при угле крена θ ≥ 30º. Так как судно, рассматриваемое мною, имеет длину 95.25 м, величина плеча определяется линейной интерполяцией:

L₂ = 105

L₁ = 80

L = 95.25

δl = (L₂ – L₁/L₂ – L)· L₂ – L₁

l = 0.20 + (L₂ – L₁) = 0.20 + 0.01 = 0.21 м

Определяем максимальное плечо статической остойчивости по рис. 9

L_max = 0.68 м

L_max > 0.21 м

Судно прошло проверку соответствия ДСО требованиям Морского регистра.

8.1.Проверка соответствия диаграммы динамической остойчивости требованиям Морского регистра.

S_m = 0.093 м·рад > 0.055 м·рад

S_m+n

8.2.

Исправленная начальная метацентрическая высота всех судов при всех вариантах нагрузки, за исключением «судна порожнем» должна иметь значение не менее 0,15 м.

h = 0.4 м > 0.15 м

Проверка начальной метацентрической высоты на соответствие требованиям Правил морского регистра выполняется.

9.

Требования к остойчивости судна полностью соблюдены согласно Правилам морского регистра судоходства РФ.

1. Российский морской регистр судоходства. Санкт-Петербург. 2014