 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Б Критерии грубых погрешностей
Обработка результатов прямых равноточных видов измерений Результаты равноточных измерений получаются при многократных измерениях одного и того же истинного значения
где
Обычно величина
т.е. получается исправленный результат
Задача обработки результатов найти оценку (приближенная характеристика) истинного значения
Для оценки результата измерений, являющегося случайной величиной находят его характеристики: оценку математического ожидания
А Точечная оценка
При обработке результатов измерений необходимо воспользоваться свойствами математического ожидания и дисперсии. Оценка называется точечной, если ее значения можно представить на числовой оси геометрически в виде точки. 1 Исправленный ряд результатов ранжируется
2 Находится среднее арифметическое
3 Проверяется правильность вычислений
4 Определяется оценка среднего квадратического отклонения (с. к. о.) а) Оценка с. к. о. отдельного результата наблюдения (формула Бесселя)
Полученные точечные оценки по формулам (1.5) и (1.7) являются случайными, т.к. при повторных измерениях получим другую группу результатов, а для нее другие значения б) Оценка с. к. о. среднего арифметического
В полученной группе результатов измерений один или два наблюдения (обычно это крайние результаты в ряде) могут резко отличаться от остальных. Поэтому их следует проверить на наличие в них грубых погрешностей с целью их исключения из ряда измерений, т.к. они могут сильно искажать
Б Критерии грубых погрешностей
Задача решается статистическими методами, основанными на том, что распределение, к которому относится рассматриваемая группа наблюдений, можно считать нормальным. Cуществуют разные критерии. Рассмотрим один из них. 5 Критерий Грабса или n - критерий. Определяются расчетные значения
и сравниваются с табличными (Таблица П3.shs) tГ = f (q; k), (1.10) где q = (1 – pД) - уровень значимости, % pД - принятая доверительная вероятность, % k = (n - 1) - число степеней свободы, n - число результатов измерений. Обычно уровень значимости берется равным 5% или 10%. Если выполняется критерий ti < tГ , (1.11) то в результате Xi грубых погрешностей нет и расчет продолжается. Если критерий (1.11) не выполняется, то результат n/ = n - 1. 6 Записываются результаты точечной оценки
Следует отметить, что величины Точечные оценки результатов измерений указывают интервал значений измеряемой величины, внутри которого находится истинное значение
Но т.к.
В Интервальная оценка
При интервальной оценке определяется доверительный интервал, который накрывает истинное значение измеряемой величины (истинное значение оказывается внутри этого интервала) с заданной доверительной вероятностью pД где J (pД) = 2e - доверительный интервал; ( 7 Оценка доверительного интервала математического ожидания а) при нормальном законе распределения погрешностей
где t = f (pД) - коэффициент стандартного нормального закона распределения находится по таблице функций Лапласа (Таблица П1.shs)
Ф(t) = 0,5pД.
б) при распределении Стьюдента
где tp = f(q; k) - коэффициент Стьюдента находится по таблице распределения Стьюдента (Таблица П4.shs). При оценке доверительного интервала случайной погрешности
если
то опытное распределение считается нормальным. В противном случае пользуются распределением Стьюдента. В практике измерений доверительную вероятность при оценке доверительного интервала 8 Оценка доверительного интервала с. к. о.
где
c2В = f (k; qВ); c2Н = f (k; qН); qВ = 1– pВ; qН = 1– pН; pВ = (1 + pД)/2; pН = (1 – pД)/2; k = (n –1) – число степеней свободы ряда результатов измерений. Значения c2 находят по таблице распределения Пирсона 9 Записываются результаты измерения
При расчёте погрешностей необходимо пользоваться следующими правилами округления: 1)погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2; и одной - если первая цифра равна 3 и более; 2)результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности; 3)округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним - двумя лишними знаками.
1.2 Варианты заданий к разделу 1.1 (результаты измерений исправлены)
Примечания: 1) обработку результатов измерений необходимо провести с учётом свойств математического ожидания M(x) и дисперсии D(x) /1/; 2) номер варианта задания соответствует порядковому номеру фамилии студента в списке группы по зачётной ведомости.
1.3 Свойства математического ожидания и дисперсии
Математическое ожидание Дисперсией
В связи с тем, что единица дисперсии (единица ФВ возведённая в квадрат) неудобна для применения, на практике при точечной оценке случайной величины используется среднее квадратическое отклонение (с. к. о.)
1 Если все значения случайной величины q, не меняя их вероятности уменьшить (увеличить) на некоторое число a, то: а) математическое ожидание
б) дисперсия
2 Если все значения случайной величины q, не меняя их вероятности, умножить на некоторый множитель b (> 1 или < 1), то: а) математическое ожидание
б) дисперсия D (q) умножится на квадрат этого множителя
3 а) математическое ожидание
б) дисперсия
4 а) математическое ожидание
б) дисперсия постоянной величины a равна 0
Пример: При измерении случайной величины q с математическим ожиданием
Каждый результат уменьшается на одно и то же постоянное число a и умножается на один и тот же постоянный множитель b. Получается случайная величина
для другого ряда результатов
По формулам раздела 1.1 находится математическое ожидание Исходя из первого и второго свойств математического ожидания и дисперсии, определяются а)
б)
Величины a и b выбираются исходя из максимального уменьшения разрядов чисел первого ряда для получения второго ряда с целью упрощения вычислений. 1.4 Обработка результатов прямых неравноточных измерений
Результаты прямых неравноточных измерений получаются при повторных многократных измерениях одного и того же истинного значения измеряемой ФВ, разными наблюдателями, разными СИ, в разное время. При этом получается несколько серий таких результатов.
Проводится точечная оценка результатов серий:
Записываются результаты их точечной оценки:
После точечной оценки неравноточные измерения приводят к результатам
Для оценки наиболее вероятного значения ФВ по результатам неравноточных измерений вводится понятие “вес” для каждой серии результатов измерений в общей их совокупности, т. е. проводится оценка степени их доверия для получения значения измеряемой ФВ, наиболее близкого к истинному. Таким образом, понятие “вес” отражает степень доверия к результату измерения. Чем больше степень доверия, тем больше число, выражающее этот “вес”. Среднее взвешенное значение
где
“Веса” серий результатов можно определить следующими способами: а) при известных
б) при неизвестных
в) при
Среднее квадратическое отклонение
Окончательный результат записывается в виде
где Доверительный интервал
где t находится по таблице функций Лапласа
где
2 Методика обработки косвенных видов измерений
При косвенных видах измерений значение искомой величины Y получают на основании прямых видов измерений величин
где 2.1 Общий случай
В уравнениях связи аргументы
………………….;
………………….;
где
Исходя из уравнений связи (2.1) необходимо найти искомый результат Y. 1 На основании формул (1.5) и (1.8) раздела 1.1 проводится точечная оценка каждого аргумента, т. е. находятся значения
2 Исходя из уравнения связи (2.1) оценивается искомый результат
3 Оценка дисперсии искомого результата
где Следует отметить, что при Произведения частных производных уравнения связи на с. к. о. результатов измерения соответствующих аргументов называются частными погрешностями косвенного измерения
Оценка коэффициента корреляции между каждой парой аргументов определяется по формуле
где Коэффициент корреляции определяет степень связи между случайными величинами. Возможные значения коэффициента корреляции лежат в интервале Коэффициент корреляции Если
Формула (2.8) обычно справедлива, когда рассматриваемые аргументы Корреляция между погрешностями аргументов чаще всего возникает в тех случаях, когда измерения выполняются одновременно и изменения влияющих величин (температуры воздуха, напряжения питания и т.п.), хотя и допустимые сами по себе, оказывают некоторое влияние на результаты наблюдений. Критерием отсутствия корреляции между рассматриваемой парой аргументов
где
4 Оценка погрешности искомого результата: а) Если число результатов, выполненных при измерении всех аргументов, превышает 25 – 30, то
где t = f (рД) - коэффициент стандартного нормального распределения находится по таблице П.1 функции Лапласа. б) При меньшем числе наблюдений пользуются распределением Стьюдента (см. табл. П-4)
где tp=f(q; kэф) - коэффициент Стьюдента. Эффективное число степеней свободы kэф определяется по формуле
где nj – число результатов прямых измерений аргумента При равном числе наблюдений всех аргументов, т.е. при n1= …= nm= n
Эффективное число степеней свободы обычно получается дробным, поэтому для отыскания величины tp данные табл. П-4 приходиться интерполировать. Окончательный результат записывается в виде
2.2 Частный случай
В уравнениях связи (2.1) значения аргументов заданы в виде
т. е. заданы своими доверительными интервалами
где При отсутствии корреляционной зависимости между погрешностями измерений аргументов (коэффициент корреляции
Формула (2.17) получена из равенства (2.8) путём умножения левой и правой частей его на коэффициент 2.3 Критерии ничтожных частных погрешностей
Оценка дисперсии косвенного результата измерения (2.8), с учётом частных погрешностей (2.6), может быть выражена через частные погрешности
В соответствии с ГОСТом 8.011-72 “Показатели точности измерения и формы представления результатов измерения” погрешность результата округляется до одной, двух значащих цифр. Это соответствует 5% изменения погрешности результата. Следовательно, изменение левой части выражения (2.19) на 5% (0,05) не повлияет на округлённое значение
Если имеется частная погрешность
Решим неравенство (2.21) относительно
т. к. в соответствии с (2.19)
и после преобразований получим
или
Формула (2.22) в метрологии называется критерием ничтожных частных погрешностей, а сами погрешности, отвечающие неравенству (2.22) называются ничтожными или ничтожно малыми. На основании ничтожных частных погрешностей (2.22) можно пренебречь целой группой частных погрешностей, если выполняется неравенство
где
2.4 Погрешности результата косвенного вида измерений для наиболее распространённых уравнений связи
1. 2. 3. 4.
5
6. Если в уравнениях связи (2.28) и (2.29) аргументы заданы своими доверительными интервалами (2.16) и (2.17), то уравнения погрешностей (2.28) и (2.29) соответственно примут вид
Примечания: 1 Во всех формулах для с. к. о. считается, что аргументы некоррелированы (независимы). 2 При возведении в степень значительно увеличивается погрешность результата, поэтому измерение величин, которые при дальнейших вычислениях возвышаются в степень, должно производится с особой точностью. 3 Величины, из которых при дальнейшей обработке извлекаются корни, могут измеряться с меньшей точностью, поскольку погрешность таких величин при обработке уменьшается.
2.5 Варианты заданий к разделу 2
Провести обработку косвенных видов измерений по заданным уравнениям связи в соответствии с данными таблицы 2.1.
Таблица 2.1 - Уравнения связи
Примечание к табл. 2.1: № варианта уравнения связи соответствует последней цифре № зачётной книжки студента. Варианты заданий аргументов Таблица 2.2 - Варианты заданий аргументов
Примечания к табл. 2.2: 1 № варианта задания соответствует порядковому номеру фамилии студента в зачетной ведомости. 2 № аргументов соответствует номерам вариантов заданий к разделу 1.1.
3 Методика расчёта статистических характеристик погрешностей СИ в эксплуатации. Определение класса точности. Для рабочих условий эксплуатации метрологические характеристики (МХ) конкретного экземпляра аналоговых средств измерений (СИ) и цифроаналоговых преобразователей (ЦАП) в соответствии с ГОСТ 8.009-84 /2/ погрешности нормируются комбинациями: систематическая (DS), случайная 1 Оценка систематической составляющей - с учетом вариации
где
DМ i= XМi - X0; DБi = XБi - X0; (3.3) где n- число результатов XМ (XБ), - без учета вариации
где 2n - число наблюдений при определении 2 Оценка среднего квадратического отклонения (с.к.о.) случайной составляющей - с учетом вариации
- без учета вариации
3 Оценка вариации
4 Наибольшее значение основной погрешности с вероятностью, близкой к единице, определяется по формуле
Предельное значение систематической составляющей основной погрешности
Таблица 3.1 - Критерии нормирования составляющих случайной погрешности
Примечания к таблице 3.1: H0 и 1)не выполняется любое из вторых неравенств, при соблюдении соответствующих первых; 2)выполняется неравенство
5 Определение класса точности СИ. При технических измерениях, когда не предусмотрено выделение Класс точности - это обобщенная МХ, определяющая различные свойства СИ и включает в себя систематическую
В основу класса точности (А) заложены следующие положения: 1) в качестве норм служат пределы допускаемых погрешностей, включающие 2)основная погрешность D0 и дополнительная DC нормируются порознь. Основная погрешность СИ формируется при нормальных условиях эксплуатации, когда влияющие величины (неинформативные параметры) равны нормам
где l – число влияющих величин. Для аналоговых СИ класс точности нормируется пределом допускаемой основной приведенной погрешностью gop
где N - предел измерения СИ N = XВ – XН; (3.10) XВ и XН - верхний и нижний пределы измерения СИ; А - класс точности СИ выбирается из следующего ряда (ближайшее большее): (1.0; 1.5; (1.6); 2.0; 2.5; (3,0); 4,0; 5.0; и 6.0)×10n; n = 1; 0; (-1); (-2). Предельное значение основной погрешности Dop в выражении (3.9) вычисляется следующим образом: а) если случайная составляющая основной погрешности (
б) если - при отсутствии вариации (Hо - не нормируется)
- при наличии вариации (Hо - нормируется)
В формулах (3.12) и (3.13) коэффициент k зависит от принятой доверительной вероятности pД. При pД = 0,96; k = 2.
Таблица 3.2 - Варианты заданий к разделу 3
Примечания к табл. 3.1: 1 В таблице введены следующие обозначения: P0 – действительные значения измеряемого давления; PМ и PБ – результаты измерений, полученные со стороны соответственно меньших и больших значений до значения P0; N – предел измерения СИ. 2 № варианта задания соответствует последней цифре № зачётной книжки студента.
4 Методика построения функциональных схем автоматизации технологических процессов
При разработке схем систем автоматизации применяют различные средства измерения, соединяемые между собой и с объектом управления по определенным схемам. Функциональные схемы отражают функционально - блочную структуру отдельных узлов автоматического контроля, сигнализации, управления и регулирования технологического процесса и определяют оснащение объекта управления приборами и средствами автоматизации. Построение функциональной схемы системы автоматизации заключается в размещении на технологической схеме и в соответствующих местах связанных между собой датчиков и вторичной аппаратуры (показывающей, регистрирующей или регулирующей). 4.1 Виды и типы схем автоматизации
При разработке схем автоматического управления и технологического контроля применяются различные приборы и средства автоматизации, соединяемые с объектом управления и между собой по определённым схемам. В зависимости от используемых приборов и средств автоматизации схемы автоматизации различаются по видам и типам. По видам подразделяются на: 1) электрические; 2) пневматические; 3) гидравлические; 4) комбинированные. Наиболее распространённым видом являются электрические схемы. По типам подразделяются на: 1) структурные - отражают укрупненную структуру систем управления и взаимосвязи между пунктами контроля и управлением объектов и отдельными должностными лицами; 2) функциональные - отражают функциональную структуру отдельных узлов автоматического контроля, управления и регулирования технологическими процессами, и определяют оснащение объектов управления приборами и средствами автоматизации; 3) принципиальные – определяют полный состав, входящих в отдельный узел автоматизации, элементов, модулей вспомогательной аппаратуры и связей между ними и дают детальное представление о принципе его работы; 4) монтажные - показывают соединения электрических и трубных проводок в пределах комплектных устройств, а также места их присоединения и ввода; 5) соединений - показывают внешние, электрические и трубные связи между измерительными устройствами и средствами получения измерительной информации с одной стороны, со щитами и пультами автоматизации - с другой стороны.
4.2 Функциональные схемы автоматизации (ФСА)
В основу условных обозначений по ГОСТ 21.404-85 положены буквенные обозначения в сочетании с простыми графическими обозначениями. Функциональные схемы автоматизации представляют собой чертеж, на котором схематически условными обозначениями изображены: - технологическое оборудование; - коммуникации; - органы управления и средств автоматизации (приборы, регуляторы, вычислительные устройства, элементы телемеханики), с указанием связей между технологическим оборудованием и элементами автоматики, а также связей между отдельными элементами автоматики Вспомогательные устройства (редуктор или фильтры для воздуха, источники питания, соединительные коробки) на функциональных схемах автоматизации не показывают. ФСА технологической установки выполняют, как правило, на одном чертеже, на котором изображают аппаратуру всех систем контроля, регулирования, управления и сигнализации, относящуюся к данной технологической установке. Для сложных технологических процессов с большим объемом автоматизации, схемы могут быть выполнены раздельно по видам технологического объекта контроля и управления. Приборы и средства автоматизации имеют условные графические обозначения в сочетании с буквенными обозначениями (см. рис.4.1). Все местные измерительные и преобразовательные приборы, установленные на технологическом объекте, изображаются на фу |



 измеряемой физической величины (ФВ), одним и тем же средством измерения, одним наблюдателем, при неизменных условиях измерения. Результат измерения при этом равен
измеряемой физической величины (ФВ), одним и тем же средством измерения, одним наблюдателем, при неизменных условиях измерения. Результат измерения при этом равен , (1.1)
, (1.1) - истинное значение;
- истинное значение; и
и  - соответственно случайная и систематическая составляющие i - го результата.
- соответственно случайная и систематическая составляющие i - го результата. известная и в результат измерения вносится поправка
известная и в результат измерения вносится поправка , (1.2)
, (1.2) . (1.3)
. (1.3)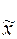 =
=  .
.  (1.4)
(1.4) - среднее значение, вокруг которого группируются все результаты и оценку среднего квадратического отклонения (с. к. о.)
- среднее значение, вокруг которого группируются все результаты и оценку среднего квадратического отклонения (с. к. о.)  , которая является мерой рассеяния результатов относительно центра группирования.
, которая является мерой рассеяния результатов относительно центра группирования. .
. (оценка математического ожидания
(оценка математического ожидания  )
)
 (1.5)
(1.5) (1.6)
(1.6) .
. (1.7)
(1.7) необходимо оценить с. к. о. среднего арифметического
необходимо оценить с. к. о. среднего арифметического  .
. (1.8)
(1.8) (1.9)
(1.9) - как промах отбрасывается и расчеты по п.1 – п.4 повторяют при новом числе наблюдений
- как промах отбрасывается и расчеты по п.1 – п.4 повторяют при новом числе наблюдений =,
=,  ,
, 
 используются при оценке погрешности окончательного результата измерения, а
используются при оценке погрешности окончательного результата измерения, а  - при оценке погрешности метода измерения.
- при оценке погрешности метода измерения. . (1.12)
. (1.12) - величины случайные, то необходимо рассмотреть вопрос о точности и надежности этой оценки, т.е. проводится их интервальная вероятностная оценка.
- величины случайные, то необходимо рассмотреть вопрос о точности и надежности этой оценки, т.е. проводится их интервальная вероятностная оценка. , (1.13)
, (1.13) )- доверительные границы.
)- доверительные границы. , (1.14)
, (1.14) , (1.15)
, (1.15) , (1.16)
, (1.16) по формулам(1.14) и (1.16) необходимо знать закон распределения случайных результатов. Приближенно это можно сделать по формуле Петерса
по формулам(1.14) и (1.16) необходимо знать закон распределения случайных результатов. Приближенно это можно сделать по формуле Петерса (1.17)
(1.17) , (1.18)
, (1.18) принимают равной pД = 0.95.
принимают равной pД = 0.95. (1.19)
(1.19) (1.20)
(1.20) , а доверительная вероятность берётся равной 0.9 (Таблица П2.shs).
, а доверительная вероятность берётся равной 0.9 (Таблица П2.shs). , при pД = 0,95,
, при pД = 0,95, при pД = 0,9.
при pД = 0,9. случайной величины q – это среднее значение, вокруг которого группируются все результаты измерения.
случайной величины q – это среднее значение, вокруг которого группируются все результаты измерения. случайной величины q называется математическое ожидание квадрата отклонения этой величины от её математического ожидания
случайной величины q называется математическое ожидание квадрата отклонения этой величины от её математического ожидания 



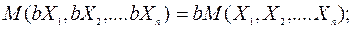
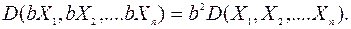


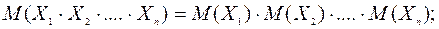

 .
.


 и дисперсия
и дисперсия  второго ряда.
второго ряда. ;
;








 измеряемой ФВ, наиболее близкое к истинному её значению
измеряемой ФВ, наиболее близкое к истинному её значению  , определяется по формуле
, определяется по формуле (1.23)
(1.23) - средние значения для отдельных серий результатов, полученных тем или иным способом;
- средние значения для отдельных серий результатов, полученных тем или иным способом; - “веса” соответствующих серий результатов.
- “веса” соответствующих серий результатов. и
и  каждой серии результатов по формуле
каждой серии результатов по формуле (1.24)
(1.24)
 (1.25)
(1.25) (одинаковые в каждой серии результатов)
(одинаковые в каждой серии результатов) . (1.26)
. (1.26) среднего взвешенного
среднего взвешенного  (1.27)
(1.27) , при pД =,
, при pД =, - абсолютная погрешность (доверительный интервал) среднего взвешенного
- абсолютная погрешность (доверительный интервал) среднего взвешенного  - при нормальном законе распределения,
- при нормальном законе распределения, ;
;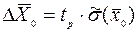 - при распределении Стьюдента,
- при распределении Стьюдента, находится по таблице Стьюдента
находится по таблице Стьюдента .
. , связанных с измеряемой известной функциональной зависимостью
, связанных с измеряемой известной функциональной зависимостью , (2.1)
, (2.1)

 (2.2)
(2.2)

 - число результатов прямых видов измерений аргументов
- число результатов прямых видов измерений аргументов  - число аргументов в уравнении связи (2.1).
- число аргументов в уравнении связи (2.1). и
и 
 (2.3)
(2.3) . (2.4)
. (2.4) , (2.5)
, (2.5) - частная производная аргумента
- частная производная аргумента  - такие коэффициенты влияния не учитываются.
- такие коэффициенты влияния не учитываются. . (2.6)
. (2.6) , (2.7)
, (2.7) - наименьшее из чисел наблюдений nk и nl соответственно аргументов
- наименьшее из чисел наблюдений nk и nl соответственно аргументов  и
и  .
. .
. тогда и только тогда, когда между результатами наблюдений
тогда и только тогда, когда между результатами наблюдений  и
и  существует линейная функциональная зависимость (погрешности измеряемых ФВ являются зависимыми).
существует линейная функциональная зависимость (погрешности измеряемых ФВ являются зависимыми). , то погрешности измерения аргументов
, то погрешности измерения аргументов  некоррелированы (погрешности измеряемых ФВ являются независимыми). В этом случае формула (2.5) примет вид
некоррелированы (погрешности измеряемых ФВ являются независимыми). В этом случае формула (2.5) примет вид . (2.8)
. (2.8) <
<  , (2.9)
, (2.9) ; (2.10)
; (2.10) - коэффициент Стьюдента находится по табл. П-4;
- коэффициент Стьюдента находится по табл. П-4; - уровень значимости;
- уровень значимости; - принятая доверительная вероятность.
- принятая доверительная вероятность. (2.11)
(2.11)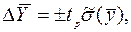 (2.12)
(2.12)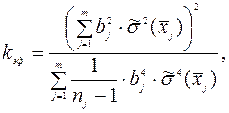 (2.13)
(2.13) (2.14)
(2.14) , при
, при  . (2.15)
. (2.15)
 ….;
….;  (2.16)
(2.16) , (2.17)
, (2.17) - коэффициент аргумента
- коэффициент аргумента  ) и при одинаковой доверительной вероятности
) и при одинаковой доверительной вероятности  ) уравнения связи (2.1), оценка погрешности
) уравнения связи (2.1), оценка погрешности  искомого результата будет иметь вид
искомого результата будет иметь вид . (2.18)
. (2.18) . Окончательный результат записывается аналогично (2.15).
. Окончательный результат записывается аналогично (2.15).
 . (2.19)
. (2.19) , т. е. при округлении справедливо равенство
, т. е. при округлении справедливо равенство . (2.20)
. (2.20) составляющая менее 5% от
составляющая менее 5% от  <
<  . (2.21)
. (2.21)
 <
< 
 <
< 



 . (2.22)
. (2.22) <
<  , (2.23)
, (2.23) - максимальная из всех частных погрешностей.
- максимальная из всех частных погрешностей. . (2.24)
. (2.24) . (2.25)
. (2.25) . (2.26)
. (2.26) . (2.27)
. (2.27) . (2.28)
. (2.28) (2.29)
(2.29) , (2.30)
, (2.30) . (2.31)
. (2.31)




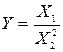






 составляющие и вариация (H), которые рассчитываются по результатам одной и той же серии наблюдений одного и того же действительного значения физической величины X0 .
составляющие и вариация (H), которые рассчитываются по результатам одной и той же серии наблюдений одного и того же действительного значения физической величины X0 . погрешности СИ
погрешности СИ (3.1)
(3.1) и
и  - средние значения погрешностей в точке результата X0 , полученные экспериментально при медленных изменениях измеряемого параметра со стороны соответственно меньших и больших значений до значения X0
- средние значения погрешностей в точке результата X0 , полученные экспериментально при медленных изменениях измеряемого параметра со стороны соответственно меньших и больших значений до значения X0
 (3.2)
(3.2) (3.4)
(3.4) .
. погрешности СИ
погрешности СИ (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7) (3.8)
(3.8) нормируется всегда, т.к. реальные СИ не могут быть изготовлены идеально точно. В свою очередь, одной из случайной составляющей основной погрешности (H0 или
нормируется всегда, т.к. реальные СИ не могут быть изготовлены идеально точно. В свою очередь, одной из случайной составляющей основной погрешности (H0 или  ) можно пренебречь, если она менее 10% другой. Критерии нормирования в соответствии с двумя неравенствами приведены в табл. 3.1.
) можно пренебречь, если она менее 10% другой. Критерии нормирования в соответствии с двумя неравенствами приведены в табл. 3.1.




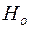
 - не нормируются, если:
- не нормируются, если: <
<  и
и  составляющих погрешности по ГОСТ 8.401-80 /3/ каждому СИ присваивается определенный класс точности (А).
составляющих погрешности по ГОСТ 8.401-80 /3/ каждому СИ присваивается определенный класс точности (А). ,
, (3.9)
(3.9)
 ) - не нормируется)
) - не нормируется) , (3.11)
, (3.11) существенна (
существенна (  - нормируется):
- нормируется): ; (3.12)
; (3.12) (3.13)
(3.13)