 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Параметра передачи четырехполюсника.
Основы теории четырехполюсников. Четырехполюсником называется электрическая схема произвольной структуры, имеющая четыре внешних зажима. (рис 1.1)
Рис.1.1 Схемное обозначение четырехполюсника.
Четырехполюсник имеет две пары зажимов 1-1' и 2-2', которые называются входами. Часто зажимы 2-2'а называют выходом, когда к ним подсоединяется нагрузка (а не источник сигнала). Будем рассматривать режим гармонических колебаний в четырехполюснике. На рис.1.1 обозначены комплексные действующие значения токов и напряжений входов. С помощью четырехполюсника моделируются различные радиотехнические устройства: транзисторы, электронные лампы, усилители, трансформаторы, линии передачи и др. Свойства четырехполюсника, внутренняя структура которого может быть не известна, описываются некоторыми параметрами, связывающими токи и напряжения его входов. Суть теории четырехполюсников заключается в том, что на основании этой теории можно связать токи и напряжения его входов не интересуясь распределением токов и напряжений внутри сколь угодно сложной схемы четырехполюсника. Классификация четырехполюсников. Четырехполюсники могут различаться по элементарной базе, а также иметь структурные различия: 1) Линейные и нелинейные четырехполюсники. Для линейных четырехполюсников, состоящий из линейных элементов (R,L,C), напряжение и ток на выходных зажимах линейно зависят от напряжения и тока на его входе. Если четырехполюсник содержит хотя бы один нелинейный элемент (диод, транзистор и др.), то он относится к классу нелинейных. Необходимо отметить, что электрические цепи с нелинейным элементом, работающим в режиме малого сигнала (например, транзисторный усилитель), могут быть представлены линейным четырехполюсником. 2) Активные и пассивные четырехполюсники. Активные четырехполюсники в отличие от пассивных содержат независимые и (или) зависимые (управляемые) источники. 3) Обратимые и необратимые четырехполюсники. Обратимые четырехполюсники позволяют передавать энергию в обоих направлениях (например RLC четырехполюсник). К необратимым четырехполюсникам относятся, например усилители, для схем, замещения которых характерно наличие управляемого источника с односторонней передачей энергии. 4) Симметричные и несимметричные четырехполюсники. В симметричном четырехполюснике, в отличие от несимметричного, нельзя различить две пары входов путем электрических измерений. Часто симметричный четырехполюсник обладает структурной симметрией относительно вертикальной оси (рис. 1.2а)
Рис 1.2. Симметричный (а) и уравновешенный четырехполюсники.
5) Уравновешенные и неуравновешенные четырехполюсники.
Параметра передачи четырехполюсника. В теории четырехполюсников рассматриваются только токи и напряжения входов:
Число различных систем уравнений равно 6 (числу сочетаний из 4 по 2 или. С). Каждая из 6 систем уравнений полностью будет определять поведение четырехполюсника по отношению к его внешним зажимам. Так как все системы уравнений описывают один и тот же четырехполюсник, то любую из них можно получить из любой другой. В дальнейшем будем рассматривать линейные четырехполюсники. Для них уравнения передачи будут линейными. 1. Уравнения передачи четырехполюсника через Y-параметры или параметры проводимости Рассмотрим систему (1.1).В ней принято, что независимые переменные напряжения входов
Где: Аналогично для тока
 + + 
Параметры (коэффициенты) уравнений имеют размерность проводимостей, а их физический смысл можно установить из рассмотрения режимов короткого замыкания входов, когда принимается
Для симметричного четырехполюсника должно выполняться равенство входных проводимостей Y11=Y22, а для обратимого – равенство передаточных проводимостей Y12=Y21. Эти утверждения следуют из определений симметричного и взаимного четырехполюсников и из физического смысла соответствующих Y-параметров. Y-параметры по понятным причинам называют также параметрами проводимостей короткого замыкания. Часто используется матричная запись рассматриваемых уравнений:
В которой используется матрица Y-параметров и матрицы столбцы токов и напряжений
Пример 1. Определить Y-параметры П-образного четырехполюсника (рис 1.3)
1 + + 2
1’ 2’
Для решения достаточно записать уравнения по методу узловых напряжений, приняв нижний узел за базисный:
Таким образом Y11=Y1+Y2; Y11=-Y2=Y21; Y22=Y2+Y3 Отметим, что для пассивного четырехполюсника Y21=Y12. При Y1=Y3 П-образный четырехполюсник будет симметричным и Y1 будет равен Y2. Параметры можно найти также из их определения. Например, Y12=
+ Y1 Y3
Из этой схемы нетрудно найти
|







 1 ,
1 ,  1 ,
1 ,  2 и
2 и  2. Принятые положительные направления этих величин указаны на рис. 1.1. Соотношения, связывающие эти четыре переменные называют уравнениями передачи четырехполюсника, а коэффициенты переменных его параметрами. При записи уравнений передачи принимают любые две переменные за независимые, а две оставшиеся за зависимые переменные и зависимые переменные выражают через независимые. Например, можно составить такую систему:
2. Принятые положительные направления этих величин указаны на рис. 1.1. Соотношения, связывающие эти четыре переменные называют уравнениями передачи четырехполюсника, а коэффициенты переменных его параметрами. При записи уравнений передачи принимают любые две переменные за независимые, а две оставшиеся за зависимые переменные и зависимые переменные выражают через независимые. Например, можно составить такую систему:

 . Их можно рассматривать как заданные воздействия, которые подключаются в виде источников напряжения к двум входам. Тогда токи входов (как реакции) можно представить по принципу наложения в виде двух слагаемых от действия каждого источника в отдельности. Например:
. Их можно рассматривать как заданные воздействия, которые подключаются в виде источников напряжения к двум входам. Тогда токи входов (как реакции) можно представить по принципу наложения в виде двух слагаемых от действия каждого источника в отдельности. Например: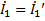 (
(  (
( 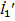 -частичный ток, вызванный воздействием только
-частичный ток, вызванный воздействием только 
 - частичный ток вызванный воздействием только
- частичный ток вызванный воздействием только 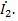 Вводя соответствующие коэффициенты, можно записать систему линейных уравнений:
Вводя соответствующие коэффициенты, можно записать систему линейных уравнений: +
+ 
 -входная проводимость со стороны входа 1 при короткозамкнутом входе 2.
-входная проводимость со стороны входа 1 при короткозамкнутом входе 2. -передаточная проводимость от входа 2 к входу 1 как отношение тока короткозамкнутого входа 1 к напряжению входа 2.
-передаточная проводимость от входа 2 к входу 1 как отношение тока короткозамкнутого входа 1 к напряжению входа 2. -передаточная проводимость от входа 1 к входу 2 как отношение тока короткозамкнутого входа 2 к напряжению входа 1.
-передаточная проводимость от входа 1 к входу 2 как отношение тока короткозамкнутого входа 2 к напряжению входа 1. -входная проводимость со стороны входа 2 при короткозамкнутом входе 1.
-входная проводимость со стороны входа 2 при короткозамкнутом входе 1. (1.3)
(1.3)

 , а схема для его определения изображена на рис. 1.4. с короткозамкнутыми зажимами 1-1’
, а схема для его определения изображена на рис. 1.4. с короткозамкнутыми зажимами 1-1’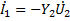 и Y12=-Y2.
и Y12=-Y2.